Atomicn number of of silver metal is 47. calculate the speed at which a beam of protons has to be fired at a sheet of silver foil if the protons were able to approach to whithin 2.5×10−14 m of the silver nucleus?
The distance between protons and slilver nucleas is
r=2.5×10−14m
Mass of proton is m,=1.67×10−27kg
Charge of protons is q!=1.6×10−19C
Atomic number of silver , Z=47
Charge of silver nueleus, q2=Ze=(47)(1.6×10−19C)
By energy conservation at a distance r the kinetic energy of proton must be equal to the potential energy of proton at that point. Thererfore we get
K=U⇒12mv2=kq1q2r
Thererfore v=√2q1q2mr
=
⎷2×(9×109)(1.6×10−19)(47)(1.6×10−19)(1.67×10−2)(2.5×10−14)=2.28×107ms−1
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.1
14 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.2
16 Videos
- ALTERNATING CURRENTBOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
63 Videos
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
Similar Questions
An α-particle after passing through a potential difference of 2×106V falls on a silver foil. The atomic number of silver is 47. Calculaye (i) the kinetic energy of the α-particle at the time of falling on the foil (ii) the kinetic energy of the α-particle at a distance of 5×10−14 m from the nucleus and (iii) the shortest distance from the nucleus of silver to which the α-particle reaches.
View SolutionAn α-particle is accelerated through a potential of 1MV and falls on a silver foil (Z=47).
Calculate : (i)Kinetic energy of the α-particle when it falls on the foil .
(ii)Kinetic energy of the α-particle when it is 6.9×10−14 m distant from the nucleus .
(iii)Distance of closest approach to the nucleus .
View Solution
Knowledge Check
A proton enters a magnetic fiedl of flux density 1.5weber/m2 with a velocity of 2×10−7m/sec at an angle of 30∘ with the field. The force on the proton will be
A0.24×10−12NB2.4×10−12NC24×10−12ND0.024×1012NAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.
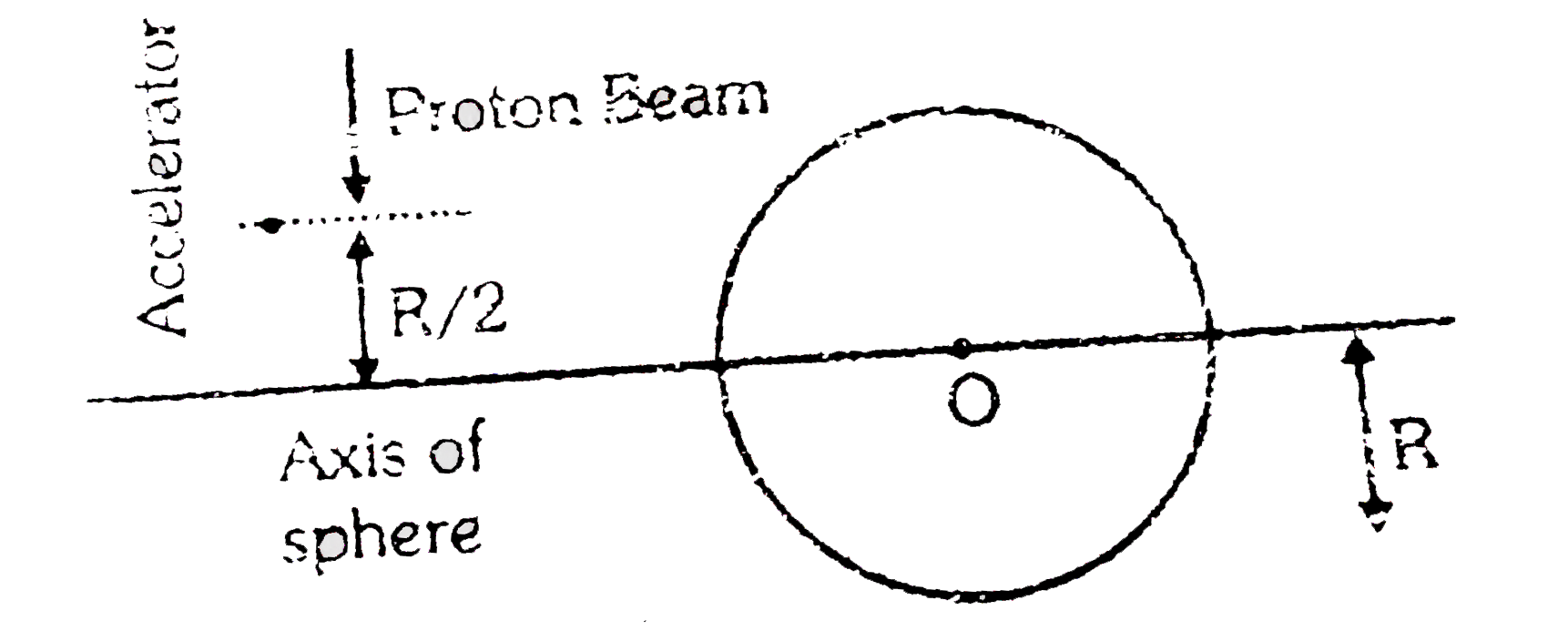
The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given byAv0Bv0/2C2v0DNone of these
Asilver and a copper voltameter are connected in parallel across a 6 V battery of neglible internal resistance .In half , 1g of copper and 2 g of silver are deposited .Calculate the rate at which the energy is supplied and 2 g of silver are that ECE of Copper is 3294×10−7gC−1 and that of silver is 1118×10−6gC−1
View SolutionCalculate the momentum of a particle which has de Broglie wavelength of 2.5×10−10m.
View SolutionCompute the electric potential at the surface of the nucleus of a silver atom. The radius of the nucleus is 3.4×10−14m and the atomic number of silver is 47.
View SolutionA beam of protons with a velocity 4×105 m/sec enters a uniform magnetic field of 0.3 Testa at an angle of 60∘ to the magnetic field. Find the radius of the helical path taken by the proton beam. Also find the pitch of the helix, which is the distance travelled by a proton in the beam parallel to the magnetic field during one period of rotation
[Mass of proton =1.67×10−27 kg. charge on proton =1.6×1019C]
View SolutionThe density of silver is 10.5 g/cc and its atomic mass is approximately 108 g . Assume each atom contributes one free electron and calcute the number of free electrons per unit volume for the silver. Resistivity of the silver is 1.6×10−8Ωm.
What potential difference must be applied across the silver wire of length 0.1 m and area of cross section 1mm2 so that a current of 2A flows through it ? what will be the current density for the wire and drift speed of electrons ?
View SolutionA brass strip of dimensions 4 cm and 6 cm has to be coated with a silver layer of 2 min thickness. Calculate the amount of charge required for the deposition of silver and the amount of magnesium deposition in another electrolytic cell when same amount of charge is passed (density of Ag = 10.5 g/cc)
View Solution
