Audible frequencies have a range 20 Hz to 20,000 Hz. Express this range in terms of wavelength λ in air. Given velocity of sound in air is 330ms−1.
To express the range of audible frequencies (20 Hz to 20,000 Hz) in terms of wavelength (λ) in air, we can use the relationship between frequency (f), wavelength (λ), and the speed of sound (v). The formula is given by:
v=f⋅λ
Where:
- v is the speed of sound in air (330 m/s),
- f is the frequency,
- λ is the wavelength.
1. Identify the given values:
- The speed of sound in air, v=330m/s.
- The frequency range: fmin=20Hz and fmax=20,000Hz.
2. Calculate the wavelength for the minimum frequency (20 Hz):
- Using the formula λ=vf:
λmin=330m/s20Hz=33020=16.5m
3. Calculate the wavelength for the maximum frequency (20,000 Hz):
- Again using the formula λ=vf:
λmax=330m/s20,000Hz=33020000=0.0165m
4. Express the range of wavelengths:
- The range of wavelengths corresponding to the audible frequency range is from λmax to λmin:
Wavelength range=0.0165m to 16.5m
Final Answer:
The range of wavelengths corresponding to the audible frequency range of 20 Hz to 20,000 Hz in air is from 0.0165 meters to 16.5 meters.
---
- v is the speed of sound in air (330 m/s),
- f is the frequency,
- λ is the wavelength.
- The speed of sound in air, v=330m/s.
- The frequency range: fmin=20Hz and fmax=20,000Hz.
- Using the formula λ=vf:
λmin=330m/s20Hz=33020=16.5m
- Again using the formula λ=vf:
λmax=330m/s20,000Hz=33020000=0.0165m
- The range of wavelengths corresponding to the audible frequency range is from λmax to λmin:
Wavelength range=0.0165m to 16.5m
The range of wavelengths corresponding to the audible frequency range of 20 Hz to 20,000 Hz in air is from 0.0165 meters to 16.5 meters.
Topper's Solved these Questions
Similar Questions
Audible frequencies have a range 20 Hz to 20,000 Hz. Express this range in terms of (i) period T (ii) wavelength λ in air and (ii) angular frequency. Given velocity of sound in air is 330ms−1
View SolutionAudible frequencies have a range 40 hertz to 30,000 hertz. Express this range in terms of
(i) period T
(ii) wavelength λ in air, and
(iii) angular frequency,
Given velocity of sound in air is 350 m s−1View SolutionAudible range of frequencies to which human car responds varies between 20 to 20,000 Hz.Express the range in terms of (i)wavelength in air and (ii)time period .
The speed of sound in air is 350ms−1.View SolutionAudible ranges of frequencies is 20 Hz to 20,000 Hz. Find the range of wavelengths corresponding to this frequency. Given, velocity of sound =340m s−1.
View SolutionFor human ears, the audible range is 20 Hz to 20,000 Hz.
View SolutionAudible ranges of frequencies is 20 Hz to 20,000 Hz. Find the range of wavelengths corresponding to this frequency. Given, velocity of sound =340m s−1.
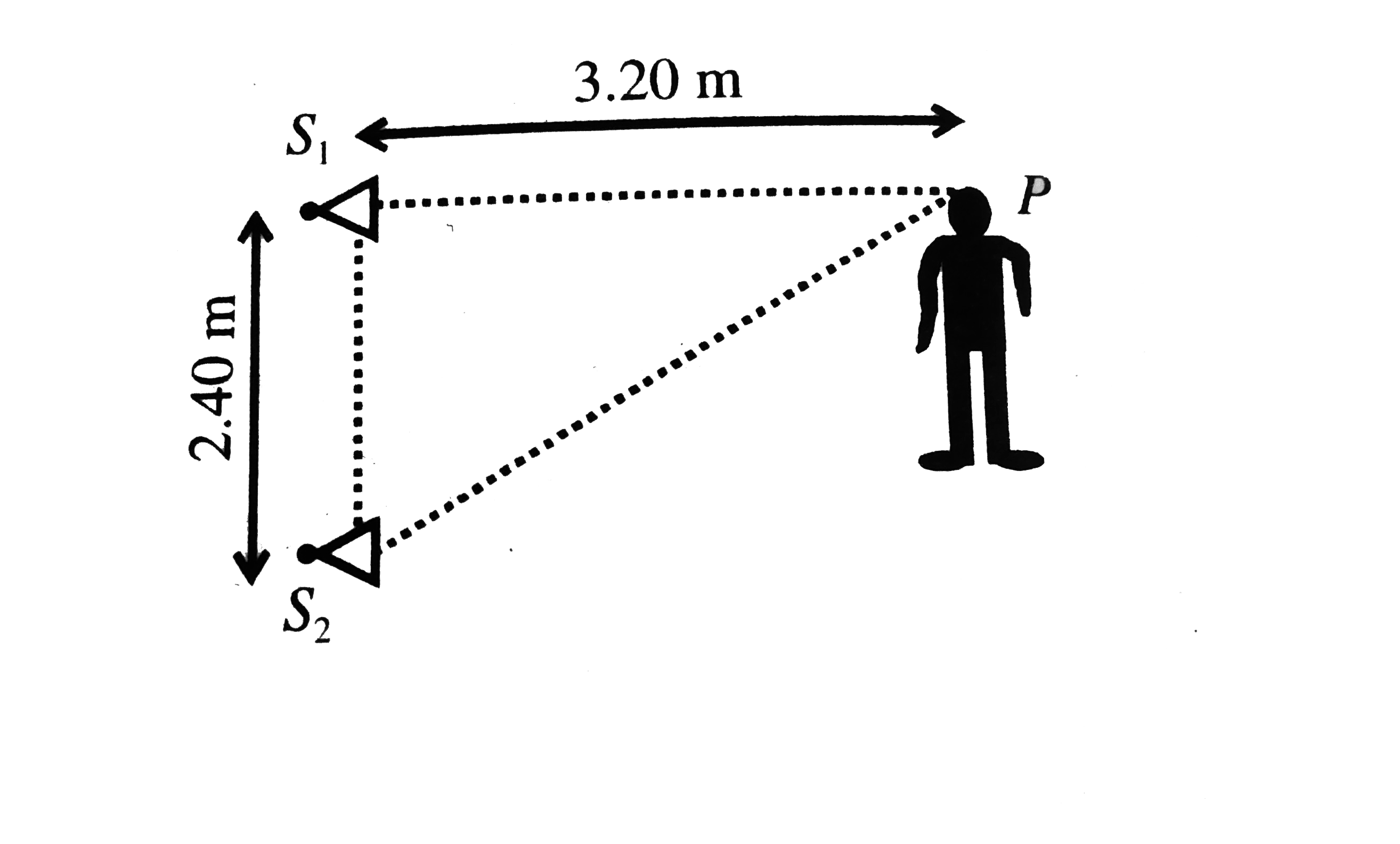
View SolutionTwo stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s.
 View Solution
View SolutionThe audible range of a human ear is 20 Hz to 20 kHz. Convert this into corresponding wavelength range. The speed of sound at ordinary temperature is 340m/s.
View SolutionA person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360ms−1.
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
 View Solution
View Solution

