Car A and car B start moving simultaneously in the same direction along the line joining them. Car A moves with a constant acceleration while car B moves with a constant velocity At time car A is behind car B. Find the time when car A overtake car B.
Given, and
Assuming car B to be rest, we have
Now, the problem can be assumed in simplified from as follows

Substituting the proper values in equation
we get, or

or
or and
Ignoring the negative value, the desired time is
Note : The above problem can also be solved without using the concept of relative motion as under.
At the time when A overtakes B,
or
Which on solving gives and , the same as we found above. As per my opinion, this approach (by taking values) is more suitable in case of two body problem in one dimensional motion. Let us see one more example in support of it.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.110videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.210videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
Two cars A and B are moving on parallel roads in the same direction. Car A moves with constant velocity 30m/s and car B moves with constant acceleration 2.5m/s2 . At , car A is ahead of car B and car B is moving with 12m/s velocity . The distance travelled by car B until it overtakes car A is
View SolutionTwo cars a and B starts motion with a velocity of 10m/s and 20m/s respectively. Car a moves with a constant acceleration of 2.5m/s2 and car B have constant acceleration of 0.5m/s2 as shown in figure. Find when car A will over take car B. Dimension of car is negligible as compare to distance. Find the time after which car A over takes car B.
View SolutionTwo cars, A and B move along the x-axis. Car A starts from rest with constant accelertion while car B moves with consstant velocity.
a. At what time s, t s, if any, do A and B have the same position?
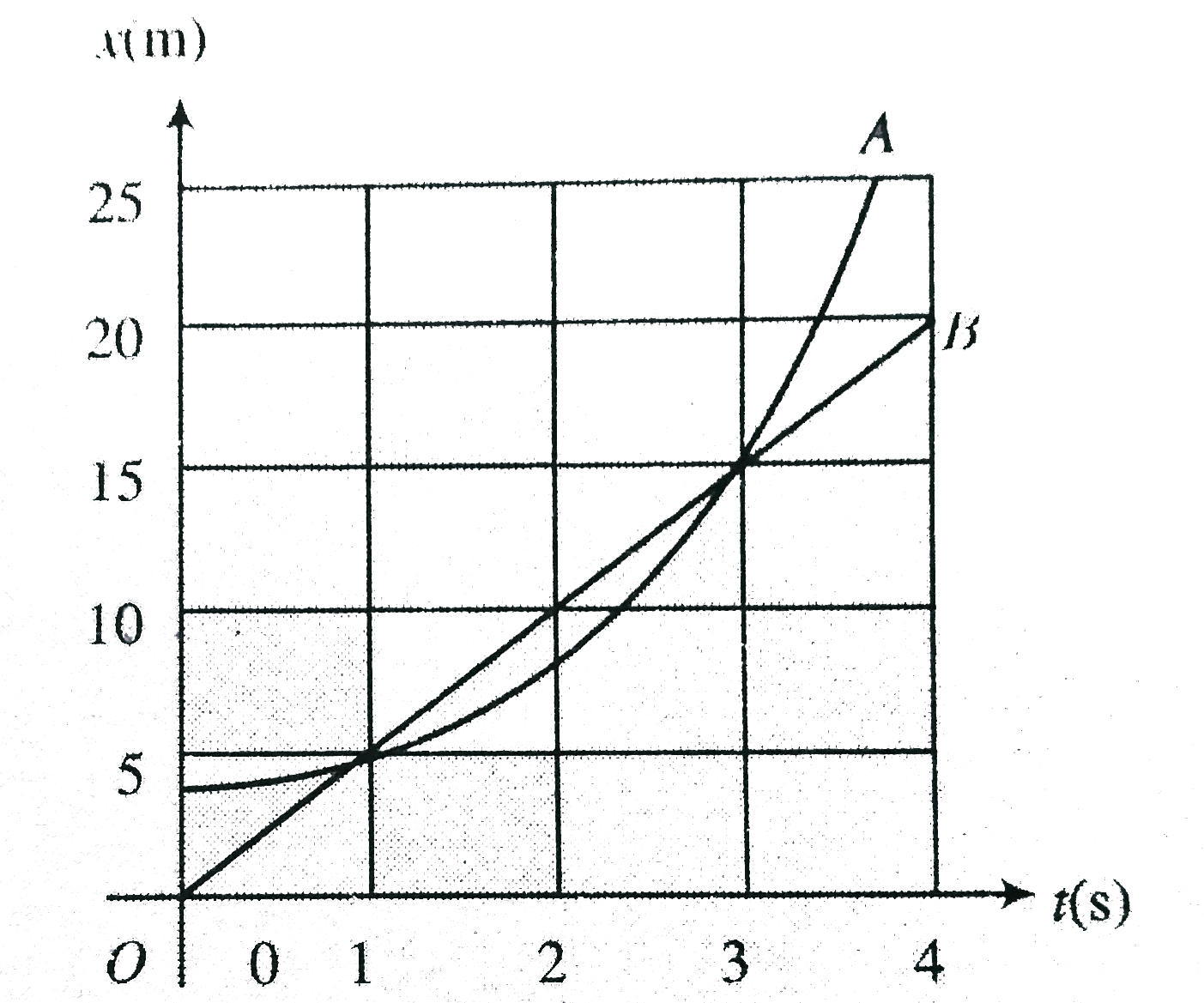 .
.
b. At what time s if any, do A and B have the same velocity? What is the velocity of car B at this time.
c. Graph velocity versus time for both A and B.
d. At what time s. If any, does car ApasscarA?<br>e.Atwˆtimes,ifanydoescarBpasscarA?View SolutionA small sphere is suspended by a string from the ceiling of a car. If the car beings to move with a constant acceleration a, the inclination of the string to the vertical is:
View SolutionA car moving with constant acceleration crosses two points A and B with velocities 10 m/s and 20 m/s in its path. Find the velocity of the car midway between A and B. (in m/s).
View SolutionTwo cars A and B are at rest at same point initially. If A starts with uniform velocity of 40 m/sec and B starts in the same direction with constant acceleration of4m/s2,then B will catch A after :
View SolutionInitially car A is 10.5m ahead of car B. Both start moving at time t=0 in the same direction along a straight line. The velocity-time graph of two cars is shown in figure. The time when the car B will catch the car A, will be.
 View Solution
View SolutionTwo cars move in the same direction along parallel roads. One of them is a 200m, long travelling with a velocity of 20m/s. The second one is 800m long travelling with a velocity of 7.5m/s. How long will it take for the first car to overtake the second car?
View SolutionTwo cars A and B start moving from the same point with same velocity v=5km/minute. Car A moves towards North and car B in moving towards East. What is the relative velocity of B with respect to A ?
View SolutionCar A has an acceleration of 2m/s2 due east and car B,4m/s2. due north. What is the acceleration of car B with respect to car A?
View Solution
