Check the correctness of the equation using dimensional analysis, where v is the critical velocity is the coefficient of viscosity, r is the radius and is the density?
The correct Answer is:The equation is correct
To check the correctness of the equation v=Kηrρ using dimensional analysis, we will analyze the dimensions of each variable involved in the equation.
1. Identify the Variables and Their Dimensions:
- v (critical velocity): The dimension of velocity is given by:
(v)=(LT−1)
- K (Reynolds number): This is a dimensionless quantity, so:
(K)=1
- η (coefficient of viscosity): The dimension of viscosity is:
(η)=(ML−1T−1)
- r (radius): The dimension of radius is:
(r)=(L)
- ρ (density): The dimension of density is:
(ρ)=(ML−3)
2. Substitute the Dimensions into the Right-Hand Side of the Equation:
The right-hand side of the equation is Kηrρ. We will substitute the dimensions we found:
(Kη)=(1)⋅(ML−1T−1)=(ML−1T−1)
Now, substituting for r and ρ:
(rρ)=(L)⋅(ML−3)=(ML−2)
3. Combine the Dimensions:
Now, we can find the dimensions of Kηrρ:
(Kηrρ)=(ML−1T−1)(ML−2)=(L1T−1)
Here, the M in the numerator and denominator cancels out.
4. Final Comparison:
Now, we compare the dimensions of the left-hand side (v) and the right-hand side (Kηrρ):
- Left-hand side: (v)=(LT−1)
- Right-hand side: (Kηrρ)=(LT−1)
Since both sides have the same dimensions, we conclude that the equation is dimensionally correct.
Conclusion:
The equation v=Kηrρ is dimensionally correct.
- v (critical velocity): The dimension of velocity is given by:
(v)=(LT−1)
- K (Reynolds number): This is a dimensionless quantity, so:
(K)=1
- η (coefficient of viscosity): The dimension of viscosity is:
(η)=(ML−1T−1)
- r (radius): The dimension of radius is:
(r)=(L)
- ρ (density): The dimension of density is:
(ρ)=(ML−3)
The right-hand side of the equation is Kηrρ. We will substitute the dimensions we found:
(Kη)=(1)⋅(ML−1T−1)=(ML−1T−1)
Now, substituting for r and ρ:
(rρ)=(L)⋅(ML−3)=(ML−2)
Now, we can find the dimensions of Kηrρ:
(Kηrρ)=(ML−1T−1)(ML−2)=(L1T−1)
Here, the M in the numerator and denominator cancels out.
Now, we compare the dimensions of the left-hand side (v) and the right-hand side (Kηrρ):
- Left-hand side: (v)=(LT−1)
- Right-hand side: (Kηrρ)=(LT−1)
The equation v=Kηrρ is dimensionally correct.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM FINDING THE DIMENSION OF A PHYSICAL QUANTITY)3videos
DIMENSIONS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM DERIVATION OF FORMULAE USING DIMENSIONS)5videos
DIMENSIONS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - VERY SHORT ANSWER QUESTIONS5videos
DIMENSIONS
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
Similar Questions
Check the correctness of the equation W=12mv2−12mu2 using the dimensional analysis, where W is the work done, m is the mass of body,u-its initial velocity and v its final velocity.
View SolutionCheck the correctness of the equation y=asin2πλ(vt−x) using dimensional analysis where y is the displacement of a particle at a distance x from the origin at time t,λ- wavelength v-wave velocity, a- amplitude.
View SolutionLet us check the dimensional correctness of the relation v=u+at.
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
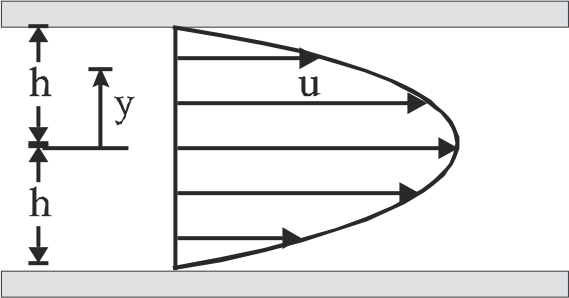
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
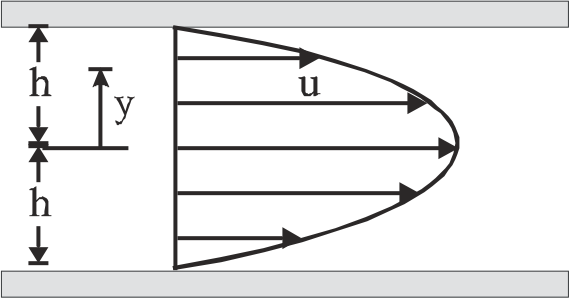
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Shear stress acting on the bottom wall isView SolutionCheck the correctness of the formula f=mv2r2 where f is force , m is mass , v is velocity and r is radius.
View SolutionWhich one of the following represents the correct dimensions of the quantity : x=ηρ, where η=coefficient of visocosity and ρ =the density of a liquid?
View SolutionThe viscous drug on a sphere of medis, moving through a fluid with velocity can be expressed as6πη where η is the coefficient of viscosity of the fluid. A small sphere of radius a and density σ is released from the bottom of a column of liqaid of density ρ. If ρ ger than σ describe the motion of the sphere. Deduce an expression for
(i) initial acceleration of the sphere and
(ii) its terminal velocityView SolutionCheck the accurary of the relation C=πηr42l for couple per unit twist (C) of a wire of length (I), radius (r) and coefficient of rigidity (h).
View SolutionA student writes the equation for the capillary rise of a liquid in a tube as h=ρg2Tcosθ, where r is the radius of the capillary tube, ρ is the density of liquid, T is the surface tension and θ is the angle of contact. Check the correctness of the equation using dimensional analysis?
View Solution
