Check the correctness of the formula using dimensions: x=asin(ωt+ϕ),x− displacement, α - amplitude, ω angular velocity ϕ is an angle and it has no dimensions.
To check the correctness of the formula x=asin(ωt+ϕ) using dimensions, we will analyze the dimensions of each term involved in the equation.
Step 1: Identify the dimensions of each variable
- Displacement x: The dimension of displacement is length, denoted as (L).
- Amplitude a: The amplitude is also a measure of length, so its dimension is (L).
- Angular velocity ω: Angular velocity is defined as the rate of change of angle with respect to time. It can be expressed as:
ω=2πT
where T is the time period. Thus, the dimension of ω is:
(ω)=(T)−1
Step 2: Determine the dimensions of ωt
- The product ωt involves multiplying angular velocity by time:
(ωt)=(ω)⋅(t)=(T)−1⋅(T)=(1)
This shows that ωt is dimensionless.
Step 3: Analyze the term ϕ
- The term ϕ is given as an angle and is also dimensionless. Thus, we have:
(ϕ)=(1)
Step 4: Check the dimensions of the sine function
- The sine function sin(ωt+ϕ) takes a dimensionless argument. Therefore, the output of the sine function is also dimensionless:
(sin(ωt+ϕ))=(1)
Step 5: Combine the dimensions in the equation
- The equation can now be analyzed:
x=asin(ωt+ϕ)
- The left side x has dimensions (L).
- The right side consists of a (which has dimensions (L)) multiplied by sin(ωt+ϕ) (which is dimensionless):
(asin(ωt+ϕ))=(L)⋅(1)=(L)
Conclusion
Since both sides of the equation have the same dimensions (L), we conclude that the equation is dimensionally correct.
- Displacement x: The dimension of displacement is length, denoted as (L).
- Amplitude a: The amplitude is also a measure of length, so its dimension is (L).
- Angular velocity ω: Angular velocity is defined as the rate of change of angle with respect to time. It can be expressed as:
ω=2πT
where T is the time period. Thus, the dimension of ω is:
(ω)=(T)−1
- The product ωt involves multiplying angular velocity by time:
(ωt)=(ω)⋅(t)=(T)−1⋅(T)=(1)
This shows that ωt is dimensionless.
- The term ϕ is given as an angle and is also dimensionless. Thus, we have:
(ϕ)=(1)
- The sine function sin(ωt+ϕ) takes a dimensionless argument. Therefore, the output of the sine function is also dimensionless:
(sin(ωt+ϕ))=(1)
- The equation can now be analyzed:
x=asin(ωt+ϕ)
- The left side x has dimensions (L).
- The right side consists of a (which has dimensions (L)) multiplied by sin(ωt+ϕ) (which is dimensionless):
(asin(ωt+ϕ))=(L)⋅(1)=(L)
Since both sides of the equation have the same dimensions (L), we conclude that the equation is dimensionally correct.
Topper's Solved these Questions
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
10 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - LONG ANSWER QUESTIONS
3 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
Similar Questions
Check the correctness of the equation y=asin2πλ(vt−x) using dimensional analysis where y is the displacement of a particle at a distance x from the origin at time t,λ- wavelength v-wave velocity, a- amplitude.
View SolutionThe equation of a wave is given by
y=asinω[xv−k]
where ω is angular velocity and v is the linear velocity . The dimensions of k will be
View SolutionThe equation of a wave is given by
y=asinω[xv−k]
where ω is angular velocity and v is the linear velocity . The dimensions of k will be
View SolutionThe equation of a wave is given by Y=Asinω(xv−k), where ω is the angular velocity and v is the linear velocity. Find the dimension of k.
View SolutionThe motion of a particle in S.H.M. is described by the displacement function, x=Acos(ωt+ϕ), If the initial (t=0) position of the particle is 1cm and its initial velocity is ωcms−1, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM:x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions ?
View SolutionA particle is executing SHM given by x=Asin(πt+ϕ). The initial displacement of particle is 1cm and its initial velocity is πcm/sec. Find the amplitude of motion and initial phase of the particle.
View Solution(a) The motion of the particle in simple harmonic motion is given by x=asinωt. If its speed is u, when the displacement is x1 and speed is v, when the displacement is x2, show that the amplitude of the motion is
A=[v2x21−u2x22v2−u2]1/2
(b) A particle is moving with simple harmonic motion is a straight line. When the distance of the particle from the equilibrium position has the values x1 and x2 the corresponding values of velocity are u1 and u2, show that the period is
T=2π[x22−x21u21−u22]1/2
View SolutionThe energy E of a particle varies with time t according to the equation E=E0sin(αt).e−αtβx, where x is displacement from mean position E0 is energy at infinite position and α and β are constants .
Dimensions of sin(αtβx) are
View SolutionThe energy E of a particle varies with time t according to the equation E=E0sin(αt).e−αtβx, where x is displacement from mean position E0 is energy at infinite position and α and β are constants .
Dimensions of β are
View Solution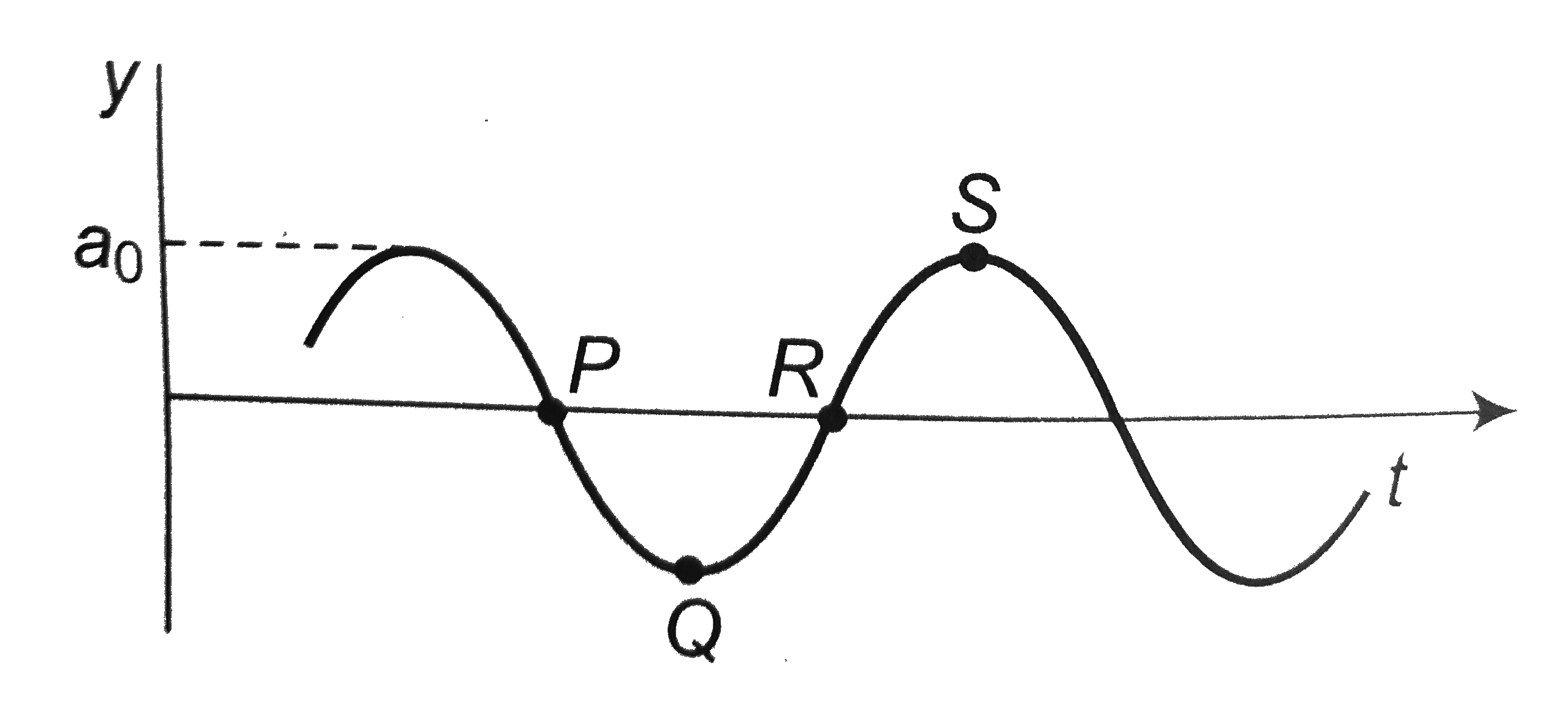
A wave motion has the function y=a0sin(ωt−kx). The graph in figure shows how the displacement y at a fixed point varies with time t. Which one of the labelled points Shows a displacement equal to that at the position x=π2k at time t=0?
View Solution
