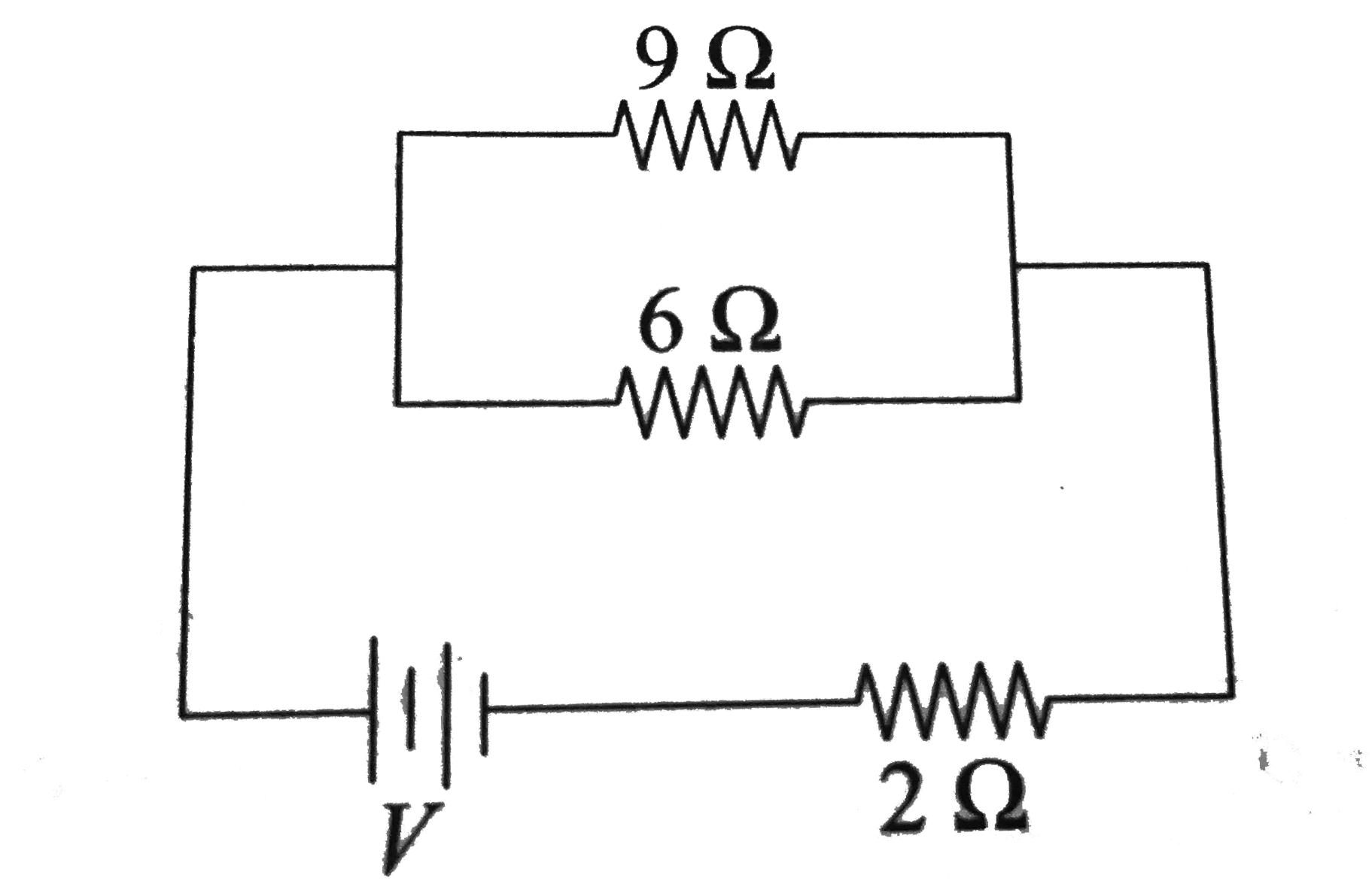
Compare the power used in the 2Ω resistor in each of the following circuits :
(i) a 6V battery in series with 1Ωand2Ω resistors, and
(ii) a 4V battery in parallel with 12Ωand2Ω resistors.
To compare the power used in the 2-ohm resistor in the two given circuits, we will analyze each circuit step by step.
Circuit (i): 6V Battery in Series with 1Ω and 2Ω Resistors
1. Identify the Circuit Configuration:
- We have a 6V battery connected in series with a 1Ω resistor and a 2Ω resistor.
2. Calculate the Total Resistance:
- The total resistance Rtotal in a series circuit is the sum of the individual resistances:
Rtotal=R1+R2=1Ω+2Ω=3Ω
3. Calculate the Current in the Circuit:
- Using Ohm's Law, the current I can be calculated as:
I=VRtotal=6V3Ω=2A
4. Calculate the Power in the 2Ω Resistor:
- The power P across a resistor can be calculated using the formula:
P=I2⋅R
- Substituting the values for the 2Ω resistor:
P=(2A)2⋅2Ω=4A2⋅2Ω=8W
Circuit (ii): 4V Battery in Parallel with 12Ω and 2Ω Resistors
1. Identify the Circuit Configuration:
- We have a 4V battery connected in parallel with a 12Ω resistor and a 2Ω resistor.
2. Calculate the Equivalent Resistance:
- For resistors in parallel, the equivalent resistance Req can be calculated using the formula:
1Req=1R1+1R2=112Ω+12Ω
- Finding a common denominator (12):
1Req=112+612=712
- Therefore, the equivalent resistance is:
Req=127Ω≈1.71Ω
3. Calculate the Total Current from the Battery:
- The total current Itotal from the battery can be calculated as:
Itotal=VReq=4V127Ω=4⋅712=2812=73A≈2.33A
4. Calculate the Current through the 2Ω Resistor:
- The voltage across the parallel resistors is the same as the battery voltage (4V). The current through the 2Ω resistor I2Ω can be calculated using Ohm's Law:
I2Ω=VR=4V2Ω=2A
5. Calculate the Power in the 2Ω Resistor:
- Using the power formula:
P=I2⋅R
- For the 2Ω resistor:
P=(2A)2⋅2Ω=4A2⋅2Ω=8W
Conclusion
- The power used in the 2Ω resistor in both circuits is:
- Circuit (i): 8W
- Circuit (ii): 8W
Thus, the power used in the 2Ω resistor in both circuits is equal.
- We have a 6V battery connected in series with a 1Ω resistor and a 2Ω resistor.
- The total resistance Rtotal in a series circuit is the sum of the individual resistances:
Rtotal=R1+R2=1Ω+2Ω=3Ω
- Using Ohm's Law, the current I can be calculated as:
I=VRtotal=6V3Ω=2A
- The power P across a resistor can be calculated using the formula:
P=I2⋅R
- Substituting the values for the 2Ω resistor:
P=(2A)2⋅2Ω=4A2⋅2Ω=8W
- We have a 4V battery connected in parallel with a 12Ω resistor and a 2Ω resistor.
- For resistors in parallel, the equivalent resistance Req can be calculated using the formula:
1Req=1R1+1R2=112Ω+12Ω
- Finding a common denominator (12):
1Req=112+612=712
- Therefore, the equivalent resistance is:
Req=127Ω≈1.71Ω
- The total current Itotal from the battery can be calculated as:
Itotal=VReq=4V127Ω=4⋅712=2812=73A≈2.33A
- The voltage across the parallel resistors is the same as the battery voltage (4V). The current through the 2Ω resistor I2Ω can be calculated using Ohm's Law:
I2Ω=VR=4V2Ω=2A
- Using the power formula:
P=I2⋅R
- For the 2Ω resistor:
P=(2A)2⋅2Ω=4A2⋅2Ω=8W
- Circuit (i): 8W
- Circuit (ii): 8W
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
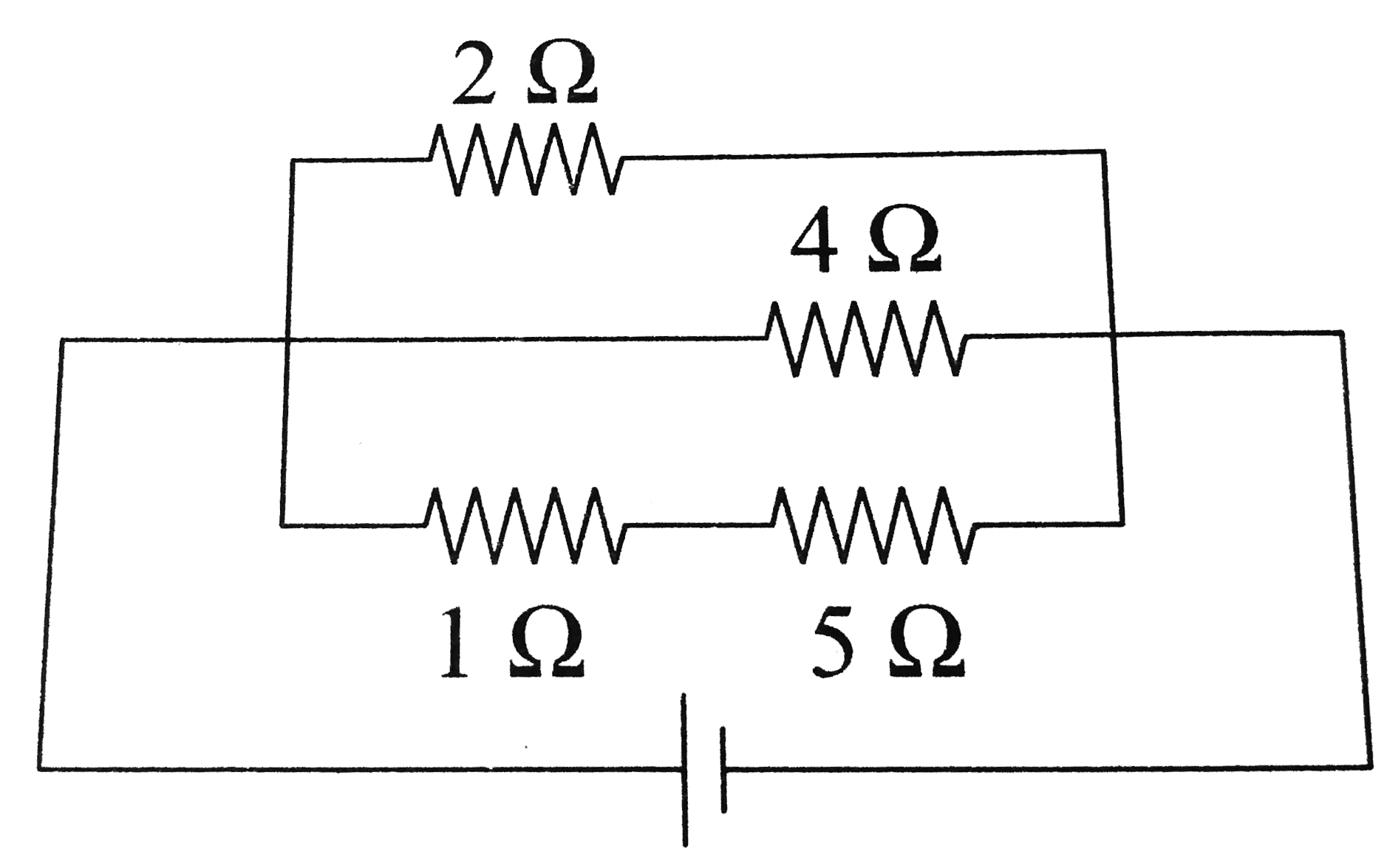 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
Power dissipated across the 8Ω resistor in the circuit shown here is 2 w. The power U dissipated in watt units across the 3Ω resistor is .
View SolutionTwo resistors of resistances 2Ωand4Ω when connected to a battery will have :
View Solution6Ω and 12Ω resistors are connected in parallel. This combination is connected in series with 10 V battery and 6Ω resistor. What is the potential differnce between the terminals of the 12Ω resistor ?
View SolutionThree resistors 8Ω,12Ωand6Ω are connected to a 12 V battery as shown in Fig. below.

the current through the 6Ω resistor.View SolutionThree resistors 8Ω,12Ωand6Ω are connected to a 12 V battery as shown in Fig. below.

the current through the 8 Ω resistor,View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 6 Ω resistor.View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current in 3 Ω resistor,View Solution