Consider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

Whenever a liquid comes in contact with solid boundaries it exerts a force on it. the force on the boundary may be obtained by integrating the pressure over the entire area of the boundary. The variations of liquid pressure acting at the base and at the wall the shown in figure a and b respectively.

1. Force at the base: Since the pressure is uniform at the base, force acting the base is given by
F=ρ× (area of the base)
since p=ρH, therefore
F=ρghH(lb)=ρg(lbH)
Since lbH=V (volume of the liquid) so
F=ρgV= weight of the liquid inside the tank
2. Force acting on the vertical wall: Pressure acting on the vertical wall is not uniform but increases linearly with depth, pressure at a depth h from the free is p−ρgh.
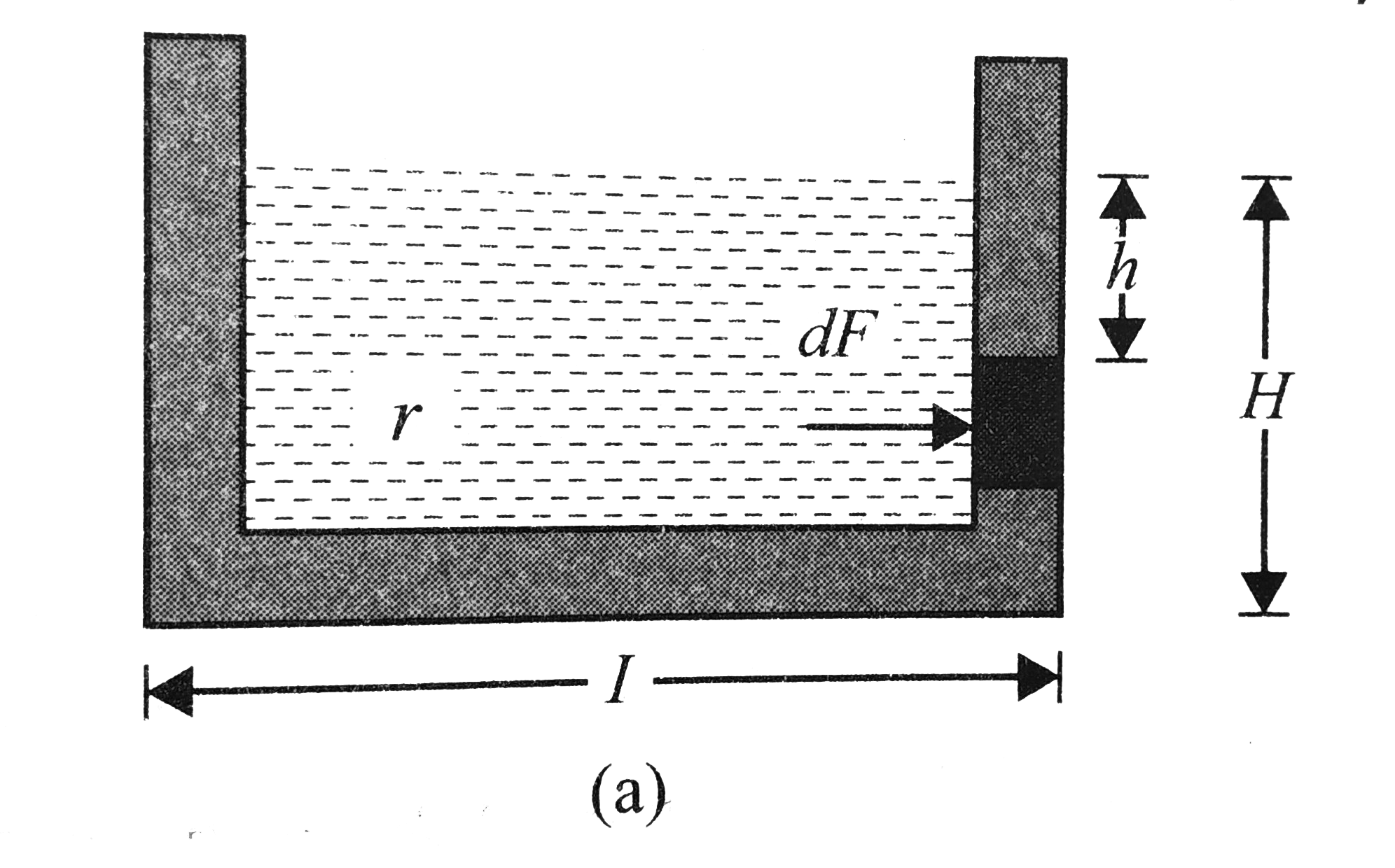
Force dF acting on a diferential element of height dh is
dF=p(bdh)=(ρgh)(bdh)=ρghdh
The total force is
F=ρgh∫H0hdh=12ρgbH2
The total force acting per unit width of the vertical wall is Fb=12ρgH2
The point of application (or the centre of force) of the total force form the free surface is given by hC=1R∫h0
Here ∫H0hdF=∫H0h(ρgpohdh)=ρgb∫H0h3dh=13ρgbH
F=12ρgbH62=→hC=23H
The total force acts at a depth 23H from the force diagram.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
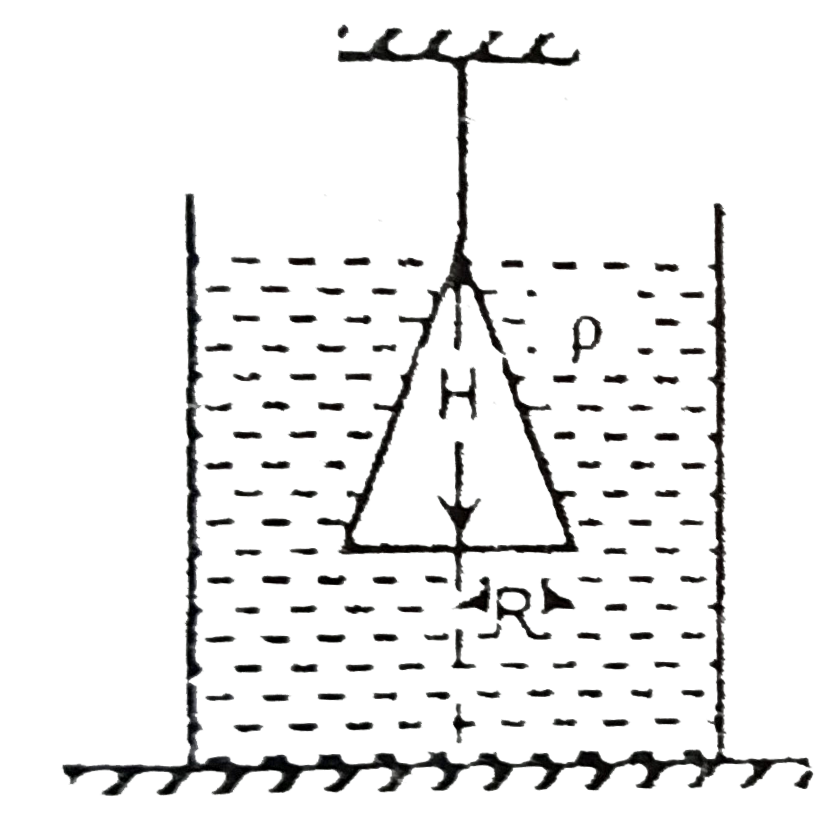
View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
View SolutionA polygenic trait is controlled by 3 genes A, B and C . In a cross AaBbCc × AaBbCc, the phenotypic ratio of the offsprings was observed as
1:6:x:20:x:6:1
What is the possible value of x ?
View SolutionA container filled with a liquid of density 4p as shown in the figure. The velocity efflux through orifice is (ρ is density of water and g = 10 ms−2)
_PHY_E05_013_Q01.png)
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height h1 (in situation 1), for which the block just starts to move up?
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
In situation 2, if h2 is further decreased, then
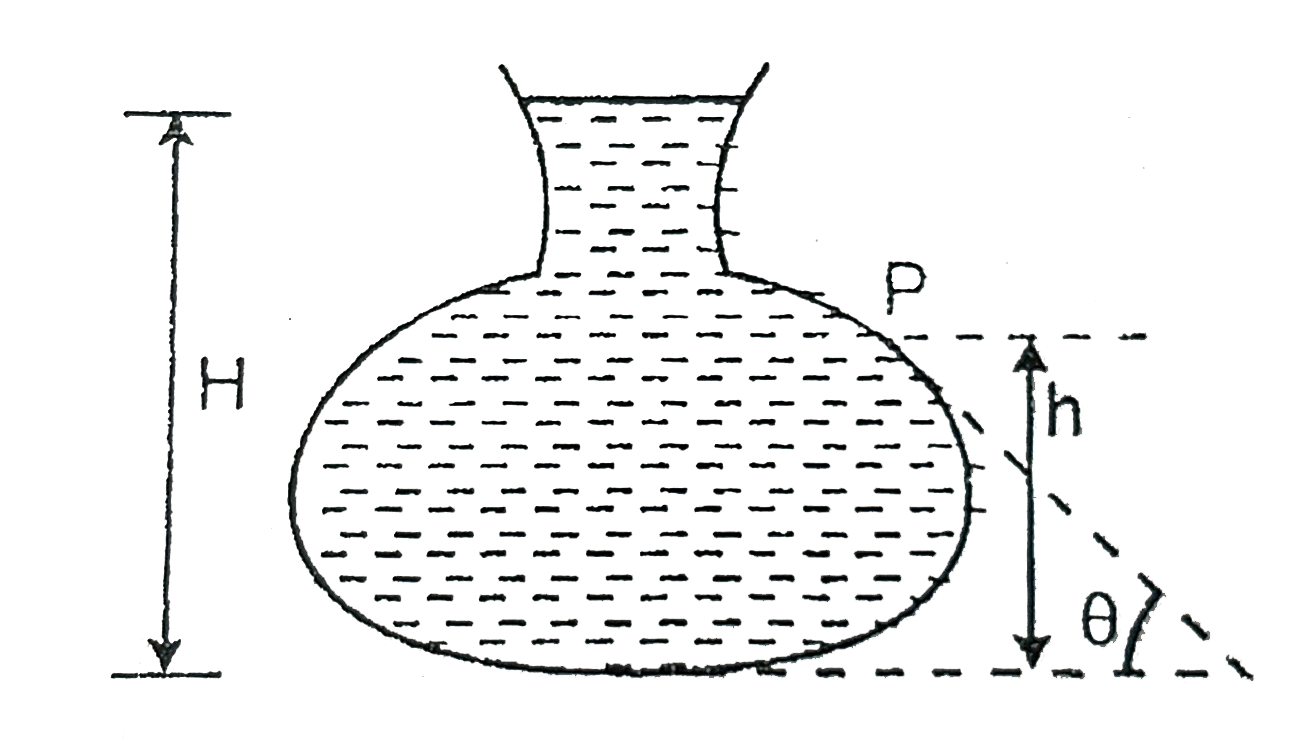
View SolutionFigure here shows the vertical cross-section of a vessel filled with a liquid of density ρ. The normal thrust per unit area on the walls vessel at point. P, as shown, will be
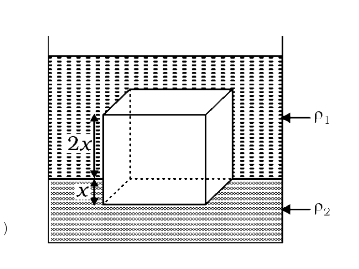
View SolutionA cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
View Solution
