Consider a uniformly charged ring of radius R. Find the pint on the axis where the electrie field is maximum.
We have the following relation for the electric field intensity of ring on a point on its axis :
E=14πε0Qr(a2+r2)3/2
E=Q4πε0r(a2+r2)3/2
let us assume the variable part of above relation as y:y=r(a2+r2)3/2 , here if y is maximum , then E being proportional , will also maximum .
dydr=(a2+r2)3/2×1−r×32(a2+r2)1/2×2r(a2+r2)3=0
⇒(a2+r2)3/2×1−r×32(a2+r2)1/2×2r=0
⇒a2+r2−3r2=0⇒r=±a√2
On substituting back in expression of electric field intensity , we get the following :
E=Q4πε0a√2(a2+a22)32
⇒E=Q4πε0a√2((3a)22)32
⇒E=Q4πε023√3a2
⇒E=23√314πε0Qa2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Consider a uniformly charged ring of radius R and total charge Q. What is the magnitude of maximum possible electric field intensity on the axis of ring? What is the distance of point from the centre of ring at which the electric field is maximum?
View SolutionCalculate distance of the point from the centre of a uniformly charged ring on its axis, where it electric field intensity becomes maximum.
View Solution
Knowledge Check
The maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
A1B2C3D4The maximum electric field at a point on the axis a uniformly charged ring is E0. At how many points on the axis will be magnitude of electric field be E0/2
A1B2C3D4An unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
 APotential at centre of ring is KQRBPotential at centre of ring is KQ√2RCPotential at centre of ring due to conducting sphere is zeroDPotential at centre of conducting sphere is KQ√2R
APotential at centre of ring is KQRBPotential at centre of ring is KQ√2RCPotential at centre of ring due to conducting sphere is zeroDPotential at centre of conducting sphere is KQ√2R
For a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionFor a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
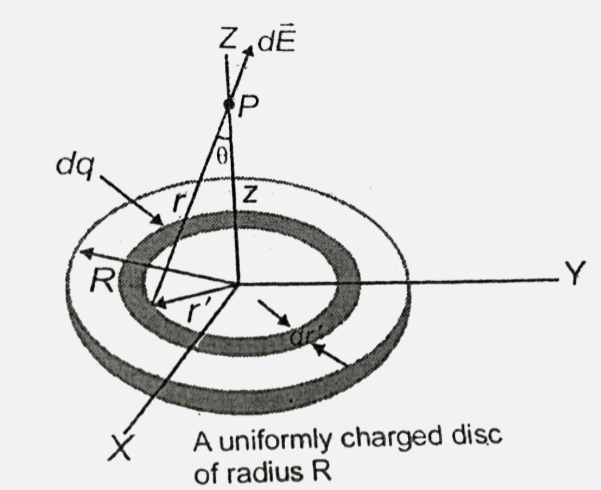
View SolutionA uniformly charged disc of radius R with a total charge Q lies in the XY -plane. Find the electric field at a point at a point P, along the Z-a xis that passes through the centre of the discc perpendicular to its plane. Discuss the limit when R>>z.
Strategy : By treating the disc as a set of concentric uniformly charged rings, the problem could be solved by using the result obtained in example for ring. Consider a ring of radius of radius r' and thickness as shown in figure.
View SolutionA point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View Solution
