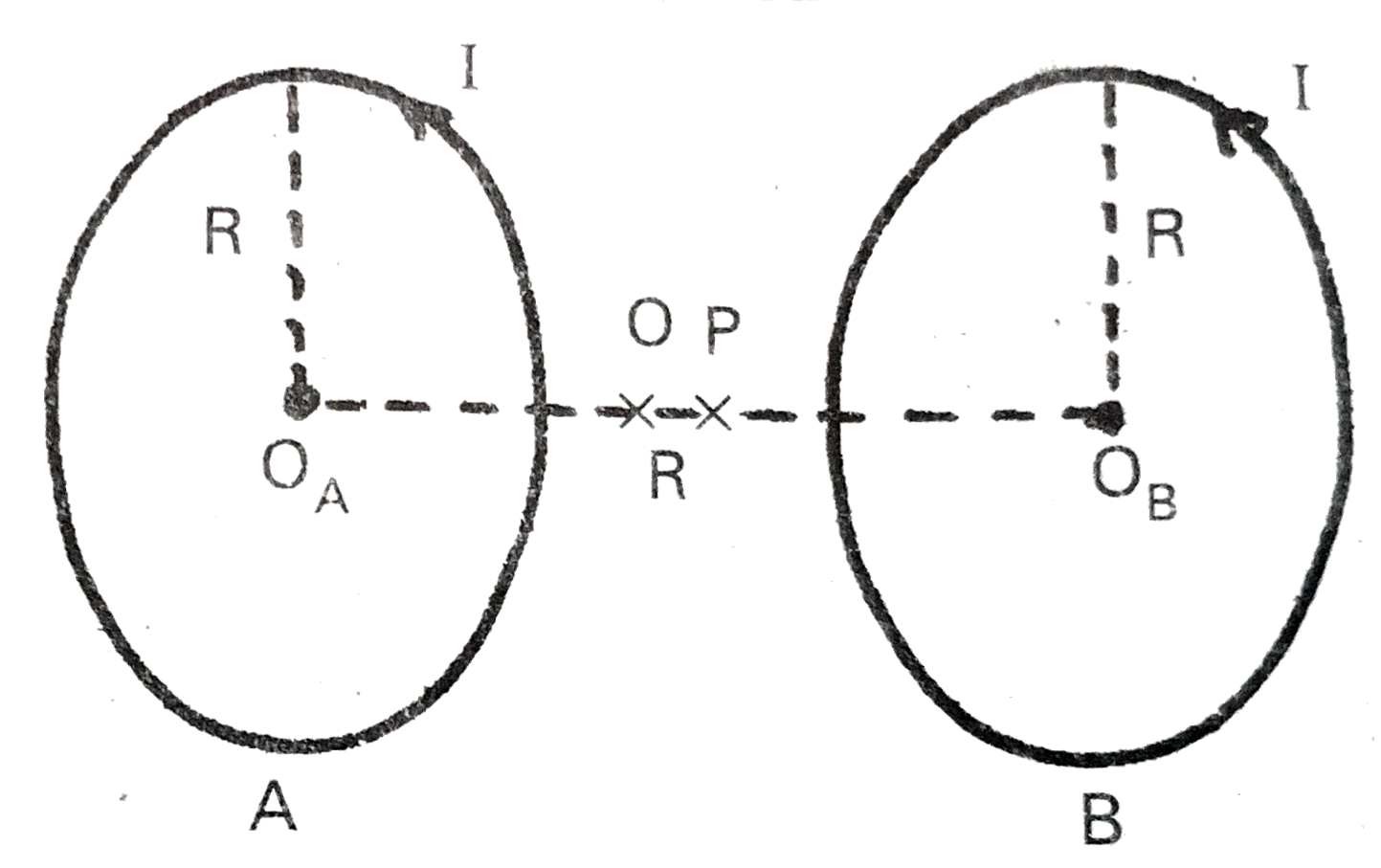
Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by B= $0.72 \frac{μ_{0} N I}{R}$ approximately.
[Such an arrnagement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils. ]

Text Solution

Verified by Experts

Radius of two parallel co-axial coils = R, number of turns =N Current =I Let the mid pints between the coils is at point O and P be the point around the mid point O. Suppose, the distance between OP=d which is very less than $R (d < < R)$ For the coil A,
$O_{A} P = \frac{R}{2} + d$
the magnetic field at point P due to coil A.
$B_{A} = \frac{μ_{0}}{4 π} . \frac{2 π n I R^{2}}{{(O_{A} P^{2} + R^{2})}_{A}^{3 / 2}}$
$= \frac{μ_{0}}{2} . \frac{N I R^{2}}{{{(R l_{2} + d)}_{2}^{2} + R^{2}}^{3 / 2}} = \frac{μ_{0} N I R^{2}}{2 {[\frac{R^{2}}{4} + d^{2} + R d + R^{2}]}^{3 / 2}}$
as according to the question $d < < R$ , so neglect turn $d^{2}$ .
$B_{A} = \frac{μ_{0} N I R^{2}}{2 {[\frac{5 R^{2} =}{4} + R d]}^{3 / 2}} = \frac{μ_{0} N I R^{2}}{2 \times {(\frac{5 R^{2}}{4})}^{3 / 2} {[1 + \frac{R \times d x x 4}{5 R^{2}}]}^{3 / 2}}$
$= \frac{μ_{0} N I R^{2} {(1 + \frac{4 d}{5 R})}^{- 3 / 2}}{2 {(\frac{5 R^{2}}{4})}^{3 / 2}} \to (1)$
The direction of $B_{A}$ is along $P O_{B}$ . According to Maxwell's right hand rule for the coil $B, O_{B} P = (R l_{2} - d)$
The magnetic field at point P due to coil B
$B_{B} = \frac{μ_{0}}{4 π} . \frac{2 π N I R^{2}}{{(O_{B} P^{2} + R^{2})}_{B}^{3 / 2}} = \frac{μ_{0}}{2} . \frac{2 N I R^{2}}{{({[\frac{R}{2} - d]}^{2} + R^{2})}^{3 / 2}}$
$= \frac{μ_{0} N I R^{2}}{2 {[\frac{R^{2}}{d} + d^{2} - R d + R^{2}]}^{3 / 2}} = \frac{μ_{0} N I R^{2} {(1 - \frac{4 d}{5 R})}^{- 3 / 2}}{2 {(\frac{5 R^{2}}{4})}^{3 / 2}}$
The direction of magnetic field $B_{B}$ is towards $P O_{B}$ . S0, the resultant magnetic field at P due to coil A and coil B is
$B = B_{A} + B_{B} = \frac{μ_{0} N I R^{2}}{2 {(\frac{5 R^{2}}{4})}^{3 / 2}} . [{(1 + \frac{4 d}{5 R})}^{- 3 / 2} + {(1 - \frac{4 d}{5 R})}^{- 3 / 2}]$
Now, use binomial theorem and neglect higher power as $d < < R$
$B = \frac{μ_{0} N I R^{2}}{2 {(\frac{5 R^{2}}{4})}^{3 / 2}} [1 - \frac{3}{2} \times \frac{4 d}{5 R} + 1 + \frac{3}{2} \times \frac{4 d}{5 R}]$
$= \frac{μ_{0} N I}{2 R} {(\frac{4}{5})}^{3 / 2} \times 2$
$= {(\frac{4}{5})}^{3 / 2} . \frac{μ_{0} N I 2}{2 R} = \frac{2 μ_{0} N I}{{(5)}^{3 / 2} .2 R} {(4)}^{3 / 2}$
$= 0.72 . \frac{μ_{0} N I}{R}$

Updated on:21/07/2023

Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
Amagnetic field is zero
Bmagnetic field is 0.8 sqrt(0.8)mu""_0I/R
Csecond derivative of magnetic field
Dfirst derivative of magnetic field $d B / d x = 0$
Two identical coils each of radius R and each carrying a current I in the same direction are placed along a common axis and separated by distance R. At the midpoint between the two coils the
Amagnetic field is zero
Bmagnetic field is 0.8 sqrt(0.8)mu""_0I/R
Csecond derivative of magnetic field
Dfirst derivative of magnetic field $d B / d x = 0$
The magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as
A $\frac{1}{r^{2}}$
B $\frac{1}{r}$
Cr
D $r^{2}$