Define angle of friction. The inclination theta of a rough plane is in

A block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, $g = 10 m / s^{2}$ )
A $\frac{3}{5}$
B $\frac{3}{4}$
C $\frac{4}{5}$
D $\frac{2}{3}$
A body is placed on a rough inclined plane of inclination $θ$ . As the angle $θ$ is the increased from $0^{\circ}$ to $90^{\circ}$ , the contact force between the block and the plane

Aremains constant
Bdecreases.
Cfirst decreases then increases
Dfirst increases then decrease.
A block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.

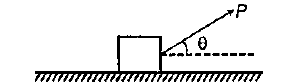A $\frac{p sin θ}{(p sin θ - ω)}$
B $\frac{p cos θ}{(ω - p sin θ)}$
C $\frac{p cos θ}{(p sin θ - ω)}$
D $\frac{p sin θ}{(ω - p sin θ)}$

A block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, $g = 10 m / s^{2}$ )