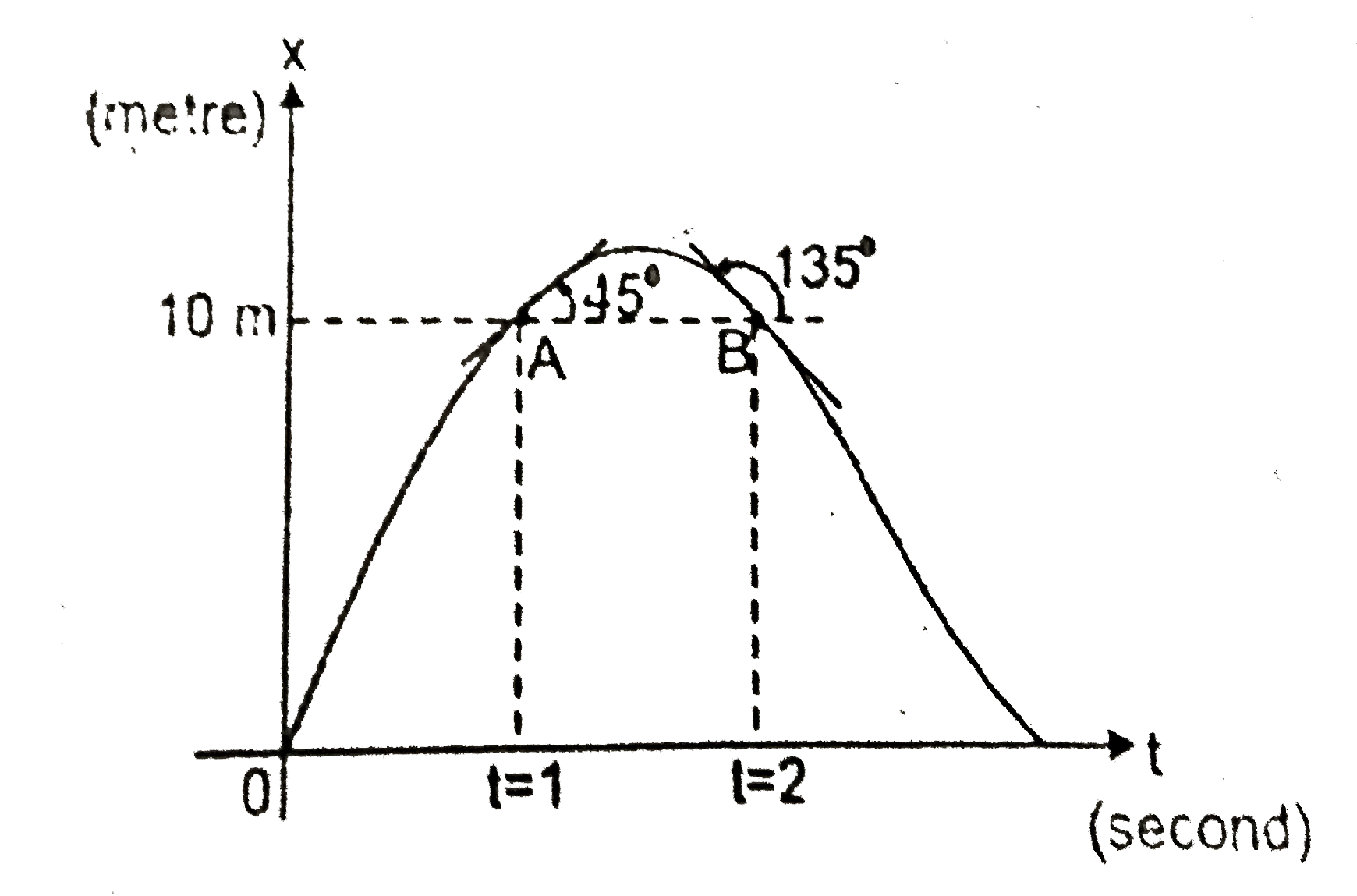
Displacement-time curve of a particle moving along a straight line is shown. Tangents at A and B makes angle 45∘ and 135∘ with positive x-axis respectively. The average acceleration of the particle during t=1,t=2 seconds is

−2m/s2
1m/s2
−1m/s2
zero
The correct Answer is:A
aav=Vf−ViΔt=(Slope at B)−(Slope at A)1s
=−1−11=−2m/s2
Topper's Solved these Questions
Similar Questions
Displacement − time curve of a particle moving along a straigh line is shown. Tangents at A and B make angles 45∘ and 135∘ with positive x− axis respectively. The average acceleratively. The average acceleration of the particle during t=1,t=2 second is :
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
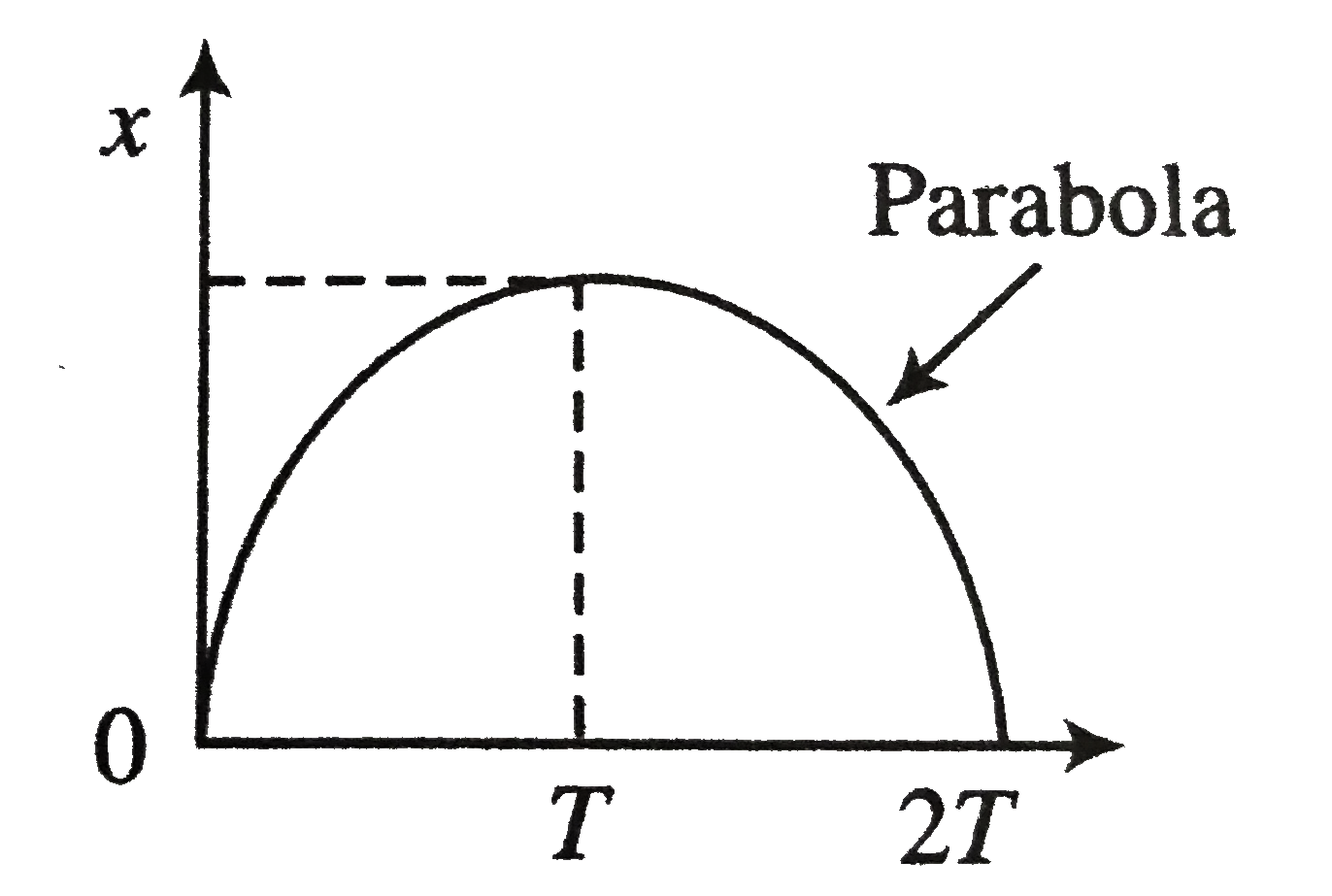
The a-t graph of the particle is correctly shown by
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
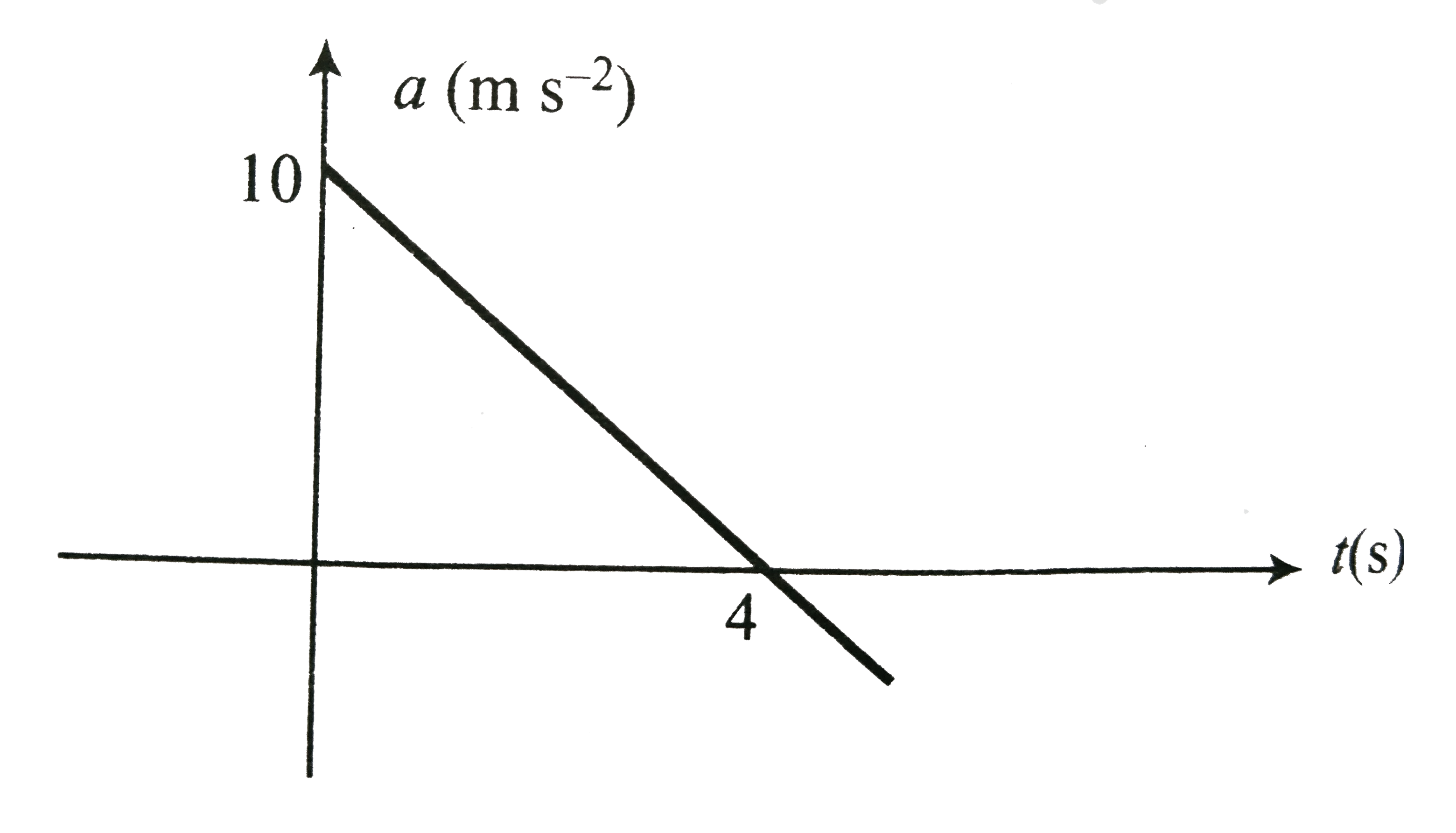 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
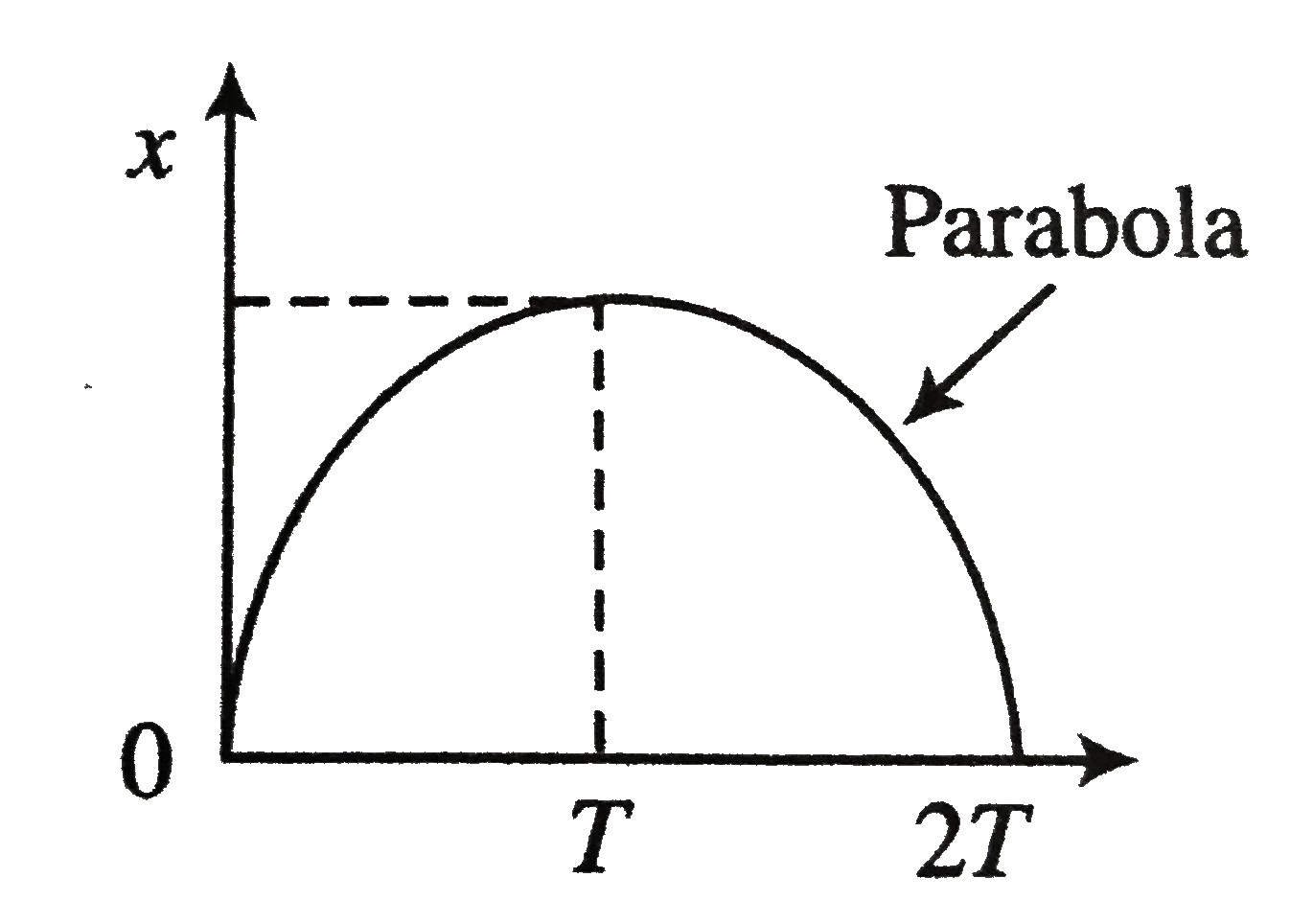
The v-t graph of the particle is correctly shown by
View Solution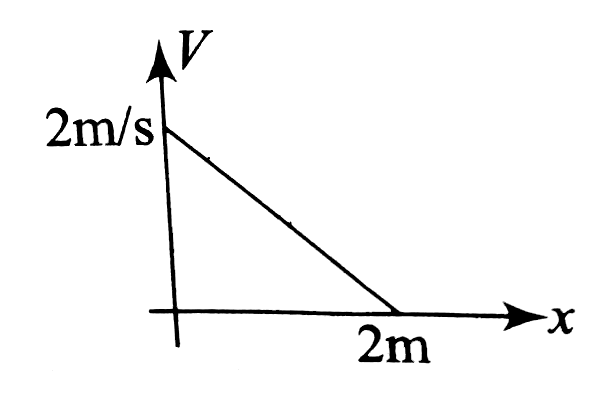
The velocity displacement graph of a particle moving along a straight line is shown in figure.
Then the acceleration displacement graph is.
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

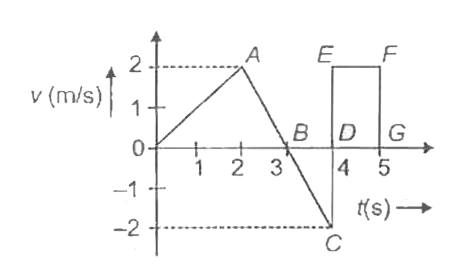
View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
The displacement of the particle in 5 second is
View Solution
