Draw a graph (not to the scale) representing the variation of square of time period (T2) with the length (l) of a pendulum.
To solve the problem of drawing a graph representing the variation of the square of the time period (T²) with the length (l) of a pendulum, we can follow these steps:
1. Understand the Relationship:
The time period (T) of a simple pendulum is given by the formula:
T=2π√lg
where l is the length of the pendulum and g is the acceleration due to gravity.
2. Square the Time Period:
To find the relationship between T2 and l, we square both sides of the equation:
T2=(2π)2⋅lg
This simplifies to:
T2=4π2g⋅l
3. Identify the Constant:
We can denote k=4π2g, which is a constant. Thus, we can rewrite the equation as:
T2=k⋅l
4. Graphing the Equation:
The equation T2=k⋅l is in the form y=mx, where y is T2, x is l, and m is the slope k. This indicates that the graph will be a straight line.
5. Draw the Axes:
- Draw the vertical axis (y-axis) and label it as T2.
- Draw the horizontal axis (x-axis) and label it as l.
6. Plot the Graph:
- Since the relationship is linear and passes through the origin (0,0), draw a straight line starting from the origin and extending upwards to the right. This line represents the direct proportionality between T2 and l.
7. Label the Graph:
- Clearly label the graph with the title "Variation of T2 with Length l".
- Optionally, you can indicate the slope k on the graph.
Final Graph:
The final graph will show a straight line passing through the origin, indicating that as the length l of the pendulum increases, the square of the time period T2 also increases linearly.
---
The time period (T) of a simple pendulum is given by the formula:
T=2π√lg
where l is the length of the pendulum and g is the acceleration due to gravity.
To find the relationship between T2 and l, we square both sides of the equation:
T2=(2π)2⋅lg
This simplifies to:
T2=4π2g⋅l
We can denote k=4π2g, which is a constant. Thus, we can rewrite the equation as:
T2=k⋅l
The equation T2=k⋅l is in the form y=mx, where y is T2, x is l, and m is the slope k. This indicates that the graph will be a straight line.
- Draw the vertical axis (y-axis) and label it as T2.
- Draw the horizontal axis (x-axis) and label it as l.
- Since the relationship is linear and passes through the origin (0,0), draw a straight line starting from the origin and extending upwards to the right. This line represents the direct proportionality between T2 and l.
- Clearly label the graph with the title "Variation of T2 with Length l".
- Optionally, you can indicate the slope k on the graph.
The final graph will show a straight line passing through the origin, indicating that as the length l of the pendulum increases, the square of the time period T2 also increases linearly.
Topper's Solved these Questions
- ICSE ANNUAL EXAMINATION -2020BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II
45 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
- LAWS OF MOTIONBOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(E) (Numericals)
31 Videos
Similar Questions
The graph between time period (T) and length (l) of a simple pendulum is
View SolutionWhich of the following graph represents the variation of resistivity (ρ) with temperature (T) for copper?
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View SolutionState how does the time period of a simple pendulum depend on length of pendulum.
View SolutionCompare the time periods of two pendulums of length 1 m and 9 m.
View SolutionTwo pendulums with identical bobs and lengths are suspended from a common support such that in rest position, the two bobs are in constact, . One of the bobs is released after being displaced by 10∘ so that it collides elastically head - on with the other bob.
(a) Describe the motion of two bobs.
(b) Draw a graph showing variation in energy of either pendulum with time,for 0≤t≤2T , where T is the period of each pendulum.
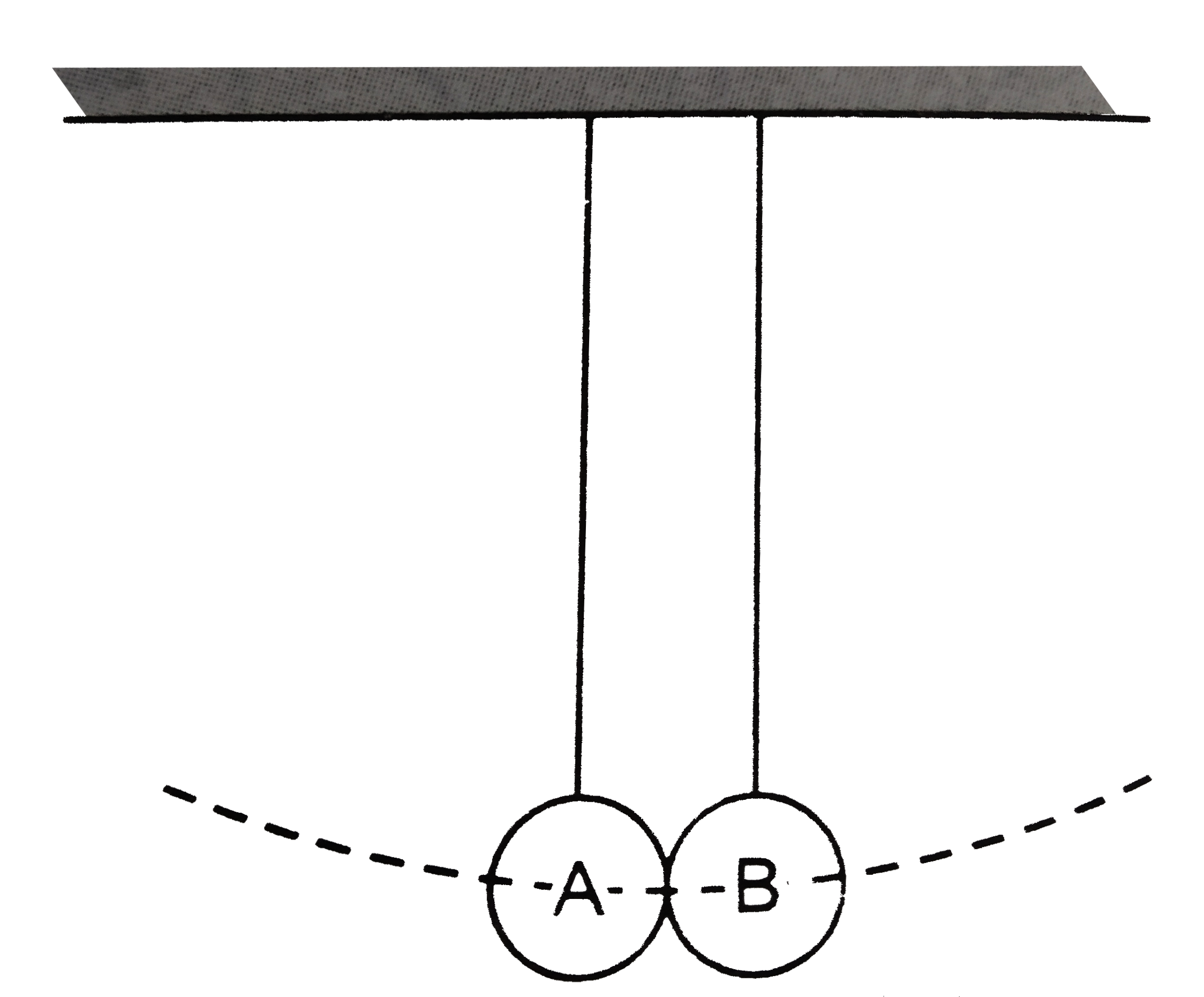
View SolutionThe graph between the length and square of the period of a simple pendulum is a
View SolutionA pendulum has time period T in air when it is made to oscillate in water it acquired a time period T=√2T The density of the pendulum bob is equal to (density) of water =1)
View SolutionA pendulum has time period T in air when it is made to oscillate in water it acquired a time period T=√2T The density of the pendulum bob is equal to (density) of water =1)
View SolutionIf the length of a simple pendulum is equal to the radius of the earth, its time period will be
View Solution
