Electric field intensity in a region of space is given by N/C. Consider a plane surface of area 10 units parallel to Y-Z plane and calculate electric flux linked through this surface.
To calculate the electric flux linked through the surface, we can follow these steps:
Step 1: Understand the Electric Flux Formula
Electric flux (Φ) is given by the formula:
Φ=→E⋅→A
where →E is the electric field vector and →A is the area vector of the surface.
Step 2: Identify the Electric Field Vector
The electric field intensity is given as:
→E=4^i+6^j+3^kN/C
Step 3: Determine the Area Vector
Since the surface is parallel to the Y-Z plane, the area vector →A will be directed along the X-axis. The magnitude of the area is given as 10 units. Therefore, the area vector can be expressed as:
→A=10^i
Step 4: Calculate the Dot Product
Now, we need to calculate the dot product →E⋅→A:
→E⋅→A=(4^i+6^j+3^k)⋅(10^i)
Using the properties of dot product:
→E⋅→A=4⋅10+6⋅0+3⋅0=40+0+0=40
Step 5: Conclusion
Thus, the electric flux linked through the surface is:
Φ=40N m2/C
Electric flux (Φ) is given by the formula:
Φ=→E⋅→A
where →E is the electric field vector and →A is the area vector of the surface.
The electric field intensity is given as:
→E=4^i+6^j+3^kN/C
Since the surface is parallel to the Y-Z plane, the area vector →A will be directed along the X-axis. The magnitude of the area is given as 10 units. Therefore, the area vector can be expressed as:
→A=10^i
Now, we need to calculate the dot product →E⋅→A:
→E⋅→A=(4^i+6^j+3^k)⋅(10^i)
Using the properties of dot product:
→E⋅→A=4⋅10+6⋅0+3⋅0=40+0+0=40
Thus, the electric flux linked through the surface is:
Φ=40N m2/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Knowledge Check
In a region of space, the electric field is given by →E=8ˆi+4ˆj+3ˆk. The electric flux through a surface of area 100 units in the xy plane is
A800 unitsB300 unitsC400 unitsD1500 unitsElectric field in a region is uniform and is given by →E−aˆi+bˆj+cˆk. Electric flux associated with a surface of area →A=πR2ˆi is
AaπR2B3aπR2C2abRDacRThe electric field intensity at all points in space is given by →E=√3ˆi−ˆj volts//metre. The nature of equipotential lines is x-y plane is given by
A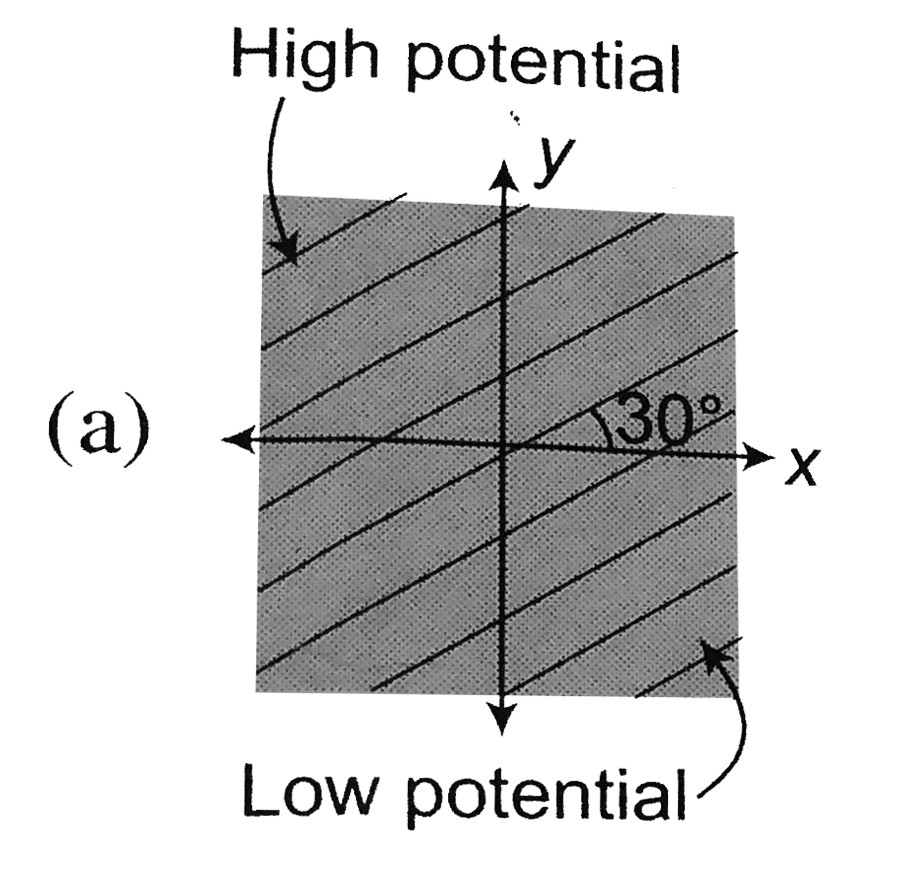 B
B C
C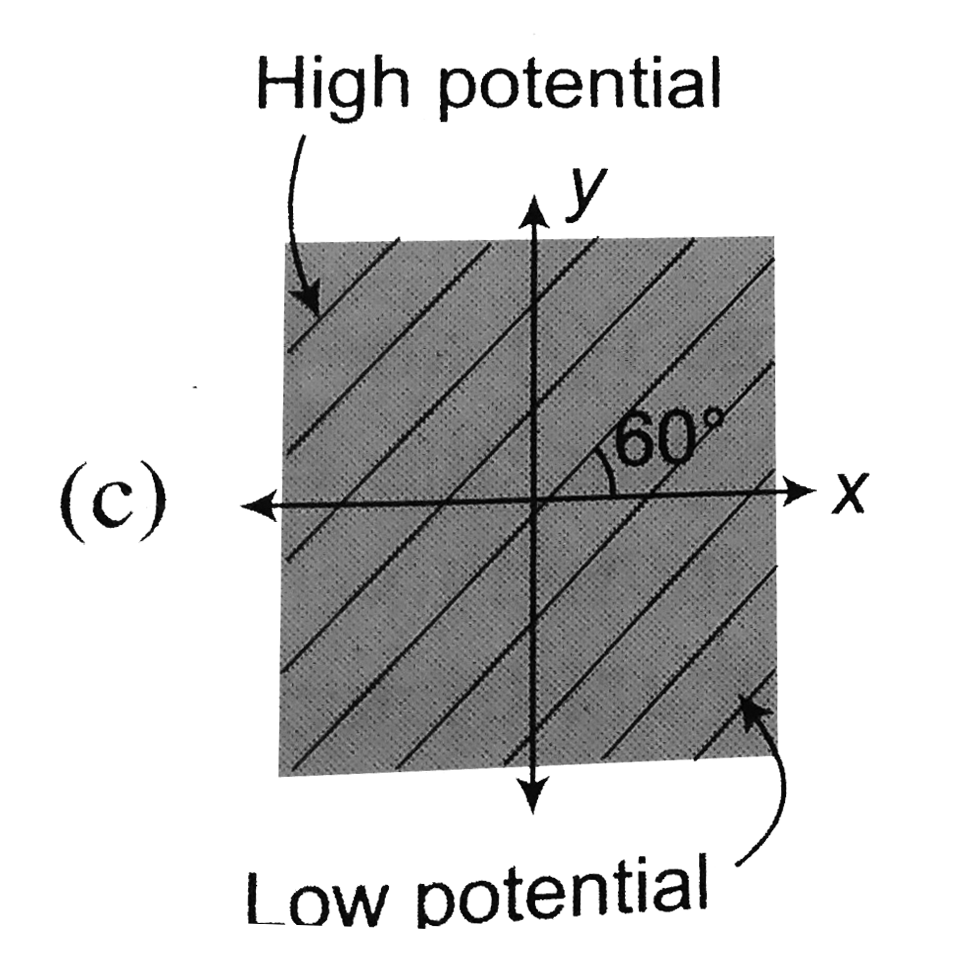 D
D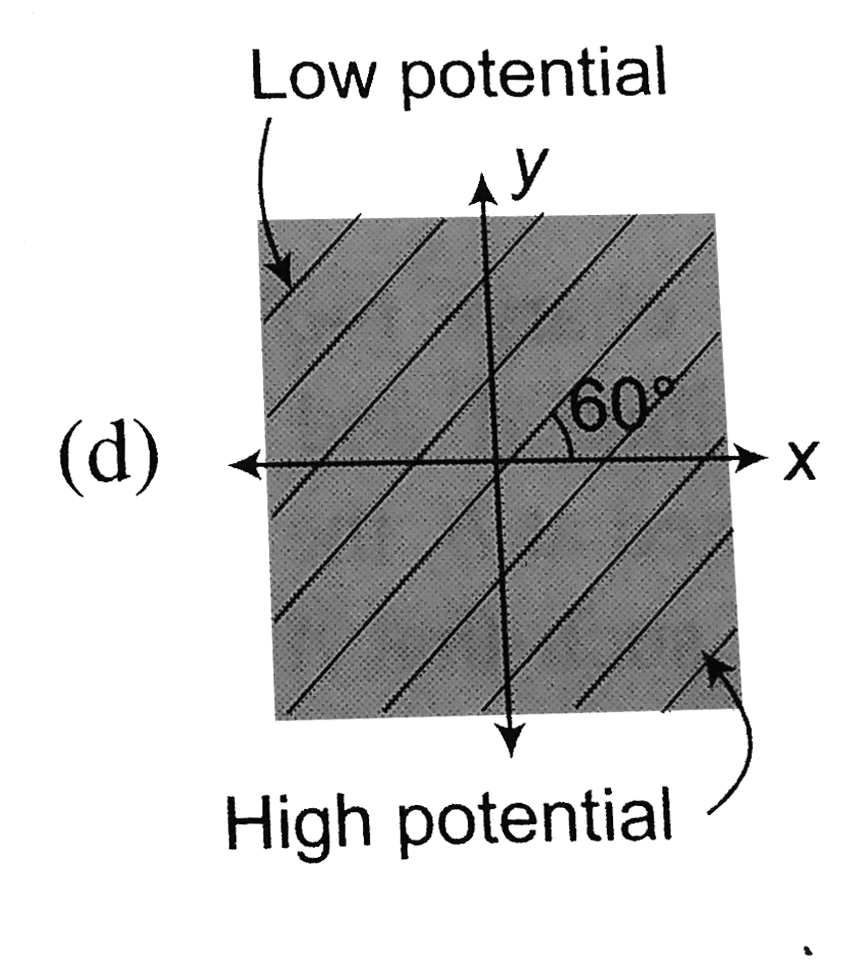
The electric field in a region of space is given ¯¯¯E=E0ˆi+2E0ˆj where E0=100NC .The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly:
View SolutionIf the electric field is given by (5ˆi+4ˆj+9ˆk)the electric flux through a surface of area 20 unit lying in the Y-Z plane will be
View SolutionIf the electric field is given by (5ˆi+4ˆj+9ˆk)the electric flux through a surface of area 20 unit lying in the Y-Z plane will be
View SolutionThe electric field in a region of space is given by E=5ˆi+2ˆjN/C. The flux of E due ot this field through an area 1m2lying in the y-z plane, in SI units is
View SolutionIf an electric field is given by 10ˆi+3ˆj+4ˆk calculate the electric flux through a surface of area 10 units lying in yz plane
View Solution
