Electric potential at origin is zero. Field in that space is 10ˆi+10ˆjNC−1. Find electric potential at (1, 1).
The correct Answer is:−20 volts
To find the electric potential at the point (1, 1) given that the electric potential at the origin is zero and the electric field in that space is E=10^i+10^jN/C, we can follow these steps:
Step 1: Understand the relationship between electric potential and electric field
The electric potential V at a point in an electric field can be calculated using the formula:
V=−∫E⋅dr
where dr is the differential displacement vector.
Step 2: Define the displacement vector
In this case, we will consider a path from the origin (0, 0) to the point (1, 1). The displacement vector can be expressed as:
dr=dx^i+dy^j
Step 3: Substitute the electric field and displacement vector into the integral
Given E=10^i+10^j, we can calculate the dot product:
E⋅dr=(10^i+10^j)⋅(dx^i+dy^j)=10dx+10dy
Step 4: Set up the integral for electric potential
Now we can set up the integral from the origin (0, 0) to (1, 1):
V=−∫(1,1)(0,0)(10dx+10dy)
Step 5: Evaluate the integral
We can break this integral into two parts:
V=−(∫1010dx+∫1010dy)
Calculating each integral:
1. For dx:
∫1010dx=10⋅(x)10=10(1−0)=10
2. For dy:
∫1010dy=10⋅(y)10=10(1−0)=10
Combining these results:
V=−(10+10)=−20V
Final Answer
Thus, the electric potential at the point (1, 1) is:
V(1,1)=−20V
---
The electric potential V at a point in an electric field can be calculated using the formula:
V=−∫E⋅dr
where dr is the differential displacement vector.
In this case, we will consider a path from the origin (0, 0) to the point (1, 1). The displacement vector can be expressed as:
dr=dx^i+dy^j
Given E=10^i+10^j, we can calculate the dot product:
E⋅dr=(10^i+10^j)⋅(dx^i+dy^j)=10dx+10dy
Now we can set up the integral from the origin (0, 0) to (1, 1):
V=−∫(1,1)(0,0)(10dx+10dy)
We can break this integral into two parts:
V=−(∫1010dx+∫1010dy)
Calculating each integral:
1. For dx:
∫1010dx=10⋅(x)10=10(1−0)=10
2. For dy:
∫1010dy=10⋅(y)10=10(1−0)=10
V=−(10+10)=−20V
Thus, the electric potential at the point (1, 1) is:
V(1,1)=−20V
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS)23videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
Similar Questions
There is a uniformly charged non conducting solid sphere made of amterial of dielectric constant one. If electric potenial at infinity be zero. Then the potential at its surface is V. if we take electric potential at its surface to be zero. Then the potential at the centre will be
View SolutionAssertion Due to two charges electric field and electric potential cannot be zero at some point simultaneously.
Reason Field is a vector quantity and electric potential is a scalar quantityView Solution
Knowledge Check
- Question 1 - Select One
The electric potential at a point in free space due to a charge Q coulomb is Q×1011 volts. The electric field at that point is
A12πε0Q×1022Vm−1B4πε0Q×1022Vm−1C12πε0Q×1020Vm−1D4πε0Q×1020Vm−1
A graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
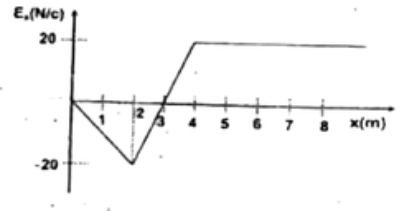
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m isView SolutionLet V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
View SolutionThe electric potential at a point in free space due to a charge Q coulomb is Q×1011 V. The electric field at that point is
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by V=4x2 volt. The electric field at the point (1m,0,2m) is ……………Vm.
View SolutionThe electric potential V at any point (x,y,z), all in meters in space is given by V=4x2 volt. The electric field at the point (1,0,2) in volt//meter is
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by V=4x2 volts. The electric field at the point (1m, 0, 2m) is……………..V/m.
View SolutionThe electric potential at a certain distance from a point charge is 600 V and the electric field is 200NC−1. Which of the following statements will be true?
View Solution
