Explain the formation of standing waves in a string clamped at both ends and discuss the various modes of vibration.
Step by step video & image solution for Explain the formation of standing waves in a string clamped at both ends and discuss the various modes of vibration. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SELF ASSESSMENT PAPER 5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-D
6 Videos
- SELF ASSESSMENT PAPER 5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-B
13 Videos
- SELF ASSESSMENT PAPER 4BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 4EXERCISE - Section-D
6 Videos
- THERMAL CONDUCTIONBOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K
2 Videos
Similar Questions
(a) Explain the formation of standing waves in an organ pipe closed at one end and discuss the various modes of vibration.
View SolutionIn a standing transerse wave on a string :
View SolutionThe vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionThe equation of a standing wave in a string fixed at both its ends is given as y=2A sin kx cos ωt. The amplitude and frequency of a particle vibrating at the point of string midway between a node and an antinode is
View SolutionDraw a diagram to show the various modes of vibration of a stretched string.
View SolutionIf a man at the equator would weight (3/5)th of his weight, the angular speed of the earth is:
View SolutionA standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
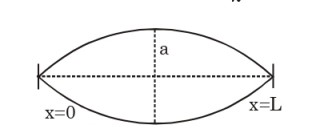
View SolutionThe equation of a standing wave produced on a string fixed at both ends is y=0.4sinπx10cos600πt where y' is measured in om 10 What could be the smallest length of string?
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
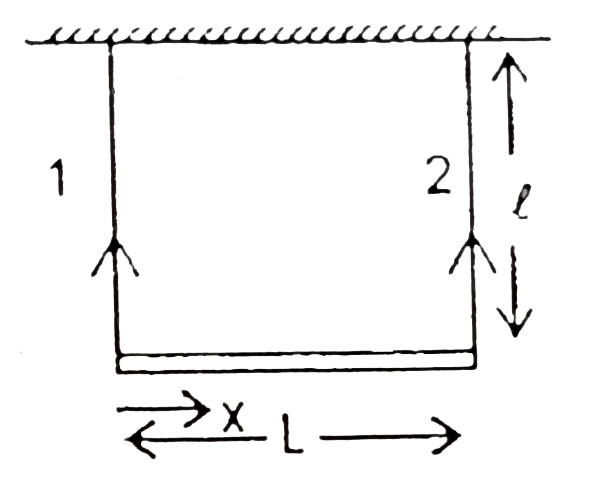
View Solution
