Find : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.
To solve the problem, we will break it down into two parts as specified in the question.
Part (i): Electric Field Intensity Due to an Infinitely Long Uniformly Charged Straight Conductor
1. Understanding the Setup: We have an infinitely long straight conductor with a uniform charge density denoted by λ (lambda) per unit length. We want to find the electric field intensity (E) at a perpendicular distance (d) from the conductor.
2. Electric Field Formula: The electric field intensity (E) due to an infinitely long charged rod can be derived using Gauss's law. The formula is given by:
E=λ2πϵ0d
where:
- λ = charge per unit length
- ϵ0 = permittivity of free space
- d = perpendicular distance from the rod
3. Conclusion for Part (i): The electric field intensity at a distance d from the infinitely long uniformly charged straight conductor is:
E=λ2πϵ0d
Part (ii): Electric Field Intensity at a Point on the Perpendicular Bisector of a Uniformly Charged Rod
1. Understanding the Setup: We have a uniformly charged rod of length l and total charge Q. The charge per unit length λ is given by:
λ=Ql
We want to find the electric field intensity at a distance d from the center of the rod, along the perpendicular bisector.
2. Electric Field Calculation:
- The electric field due to a small element dx of the rod at a distance r can be expressed. The distance from the element to the point where we are calculating the field is:
r=√d2+(l2)2
- The electric field dE due to the small charge dq=λdx is:
dE=14πϵ0⋅dqr2
- The total electric field E along the x-direction (perpendicular to the rod) can be calculated by integrating dE over the length of the rod:
Ex=∫l2−l214πϵ0⋅λdxd2+(l2)2
- Since the vertical components of the electric field from symmetrical elements will cancel out, we only need to consider the horizontal components.
3. Final Expression:
- After performing the integration, the electric field intensity at the perpendicular bisector is:
E=Q4πϵ0⋅1d√d2+(l2)2
Summary of Results
- Part (i): The electric field intensity due to an infinitely long uniformly charged straight conductor is:
E=λ2πϵ0d
- Part (ii): The electric field intensity at a point on the perpendicular bisector of a uniformly charged rod is:
E=Q4πϵ0⋅1d√d2+(l2)2
E=λ2πϵ0d
where:
- λ = charge per unit length
- ϵ0 = permittivity of free space
- d = perpendicular distance from the rod
E=λ2πϵ0d
λ=Ql
We want to find the electric field intensity at a distance d from the center of the rod, along the perpendicular bisector.
- The electric field due to a small element dx of the rod at a distance r can be expressed. The distance from the element to the point where we are calculating the field is:
r=√d2+(l2)2
- The electric field dE due to the small charge dq=λdx is:
dE=14πϵ0⋅dqr2
- The total electric field E along the x-direction (perpendicular to the rod) can be calculated by integrating dE over the length of the rod:
Ex=∫l2−l214πϵ0⋅λdxd2+(l2)2
- Since the vertical components of the electric field from symmetrical elements will cancel out, we only need to consider the horizontal components.
- After performing the integration, the electric field intensity at the perpendicular bisector is:
E=Q4πϵ0⋅1d√d2+(l2)2
- Part (i): The electric field intensity due to an infinitely long uniformly charged straight conductor is:
E=λ2πϵ0d
- Part (ii): The electric field intensity at a point on the perpendicular bisector of a uniformly charged rod is:
E=Q4πϵ0⋅1d√d2+(l2)2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Find the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionCalculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =λ) of length 2l at a distance a from the centre of the rod.
View Solution
Knowledge Check
Find the electric field at point P (as shown in figure) on the perpendicular bisector of a uniformly charged thin wire of length L carrying a charge Q. The distance of the point P from the centre of the rod is a =√32L.
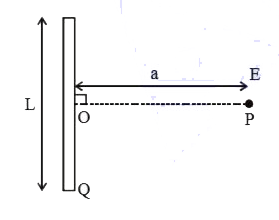 A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2
A√3Q4πε0L2BQ3πε0L2CQ2√3πε0L2DQ4πε0L2A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
AIncreases as r increases for r<Rand for r>RBZero as r increases for r<R, decreases as r increases for r>RCZero as r increases for r<R , increases as r increases for r>RDDecreases as r increases for r<Rand for r>RThe expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Aindependent of dBdirectly proportional to √dCdirectly proportional to dDdirectly proportional to 1√d
The maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R is at a distance x from the centre of the ring.The value of x is
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionDetermine electric field intensity near an infinitely long straight uniformly charge wire.
Or.
Using Gauss' law expression for electric field intensity at a point situated at a distance 'r' from an infinitely long, uniformly charged straight wire.
View SolutionDerive an expression for the strength of electric field intensity at a point on the axis of a uniformly charged circular coil of radius R carrying charge Q.
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution
