Find minimum value of l so that truck can avoid the dead end, without toppling the block kept on it.
The correct Answer is:v2g
mah2≤mgb2
a≤bhg
Final velocity of truck is zero. So that
0=v2−2(bhg)l
l=h2bv2g
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.
View SolutionFind minimum μ so that the blocks remain stationary.
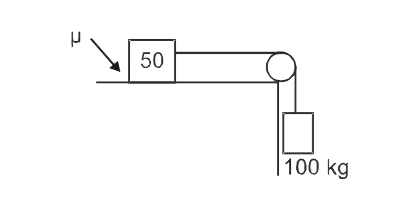View Solution
Knowledge Check
- Question 1 - Select One
A uniform box of height 2m and having a square base of side 1m, weight 150kg, is kept on one end on the floor of a truck. The maximum speed with which the truck can round a curve of radius 20m without causing the block to tip over is (assume that friction is sufficient is no sliding).
A15m/sB10m/sC8m/sDdepends on the value of coefficient of friction - Question 2 - Select One
Find the minimum value of F for which 5 kg being to slide if the coefficient of friction between the blocks is changed to 0.5 :A10 NB30 NC45 NDno value exist - Question 3 - Select One
Find minimum height of the obstacle so that the shpere can stay in equilibrium
AR1+cosθBR1+sinθCR(1−sinθ)DR(1−cosθ)
A block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
View SolutionFind the minimum value of F and the tension in the string so that the blocks move with constant velocity. The coefficient of friction at all surfaces is μ.
(a)
(b)
( c )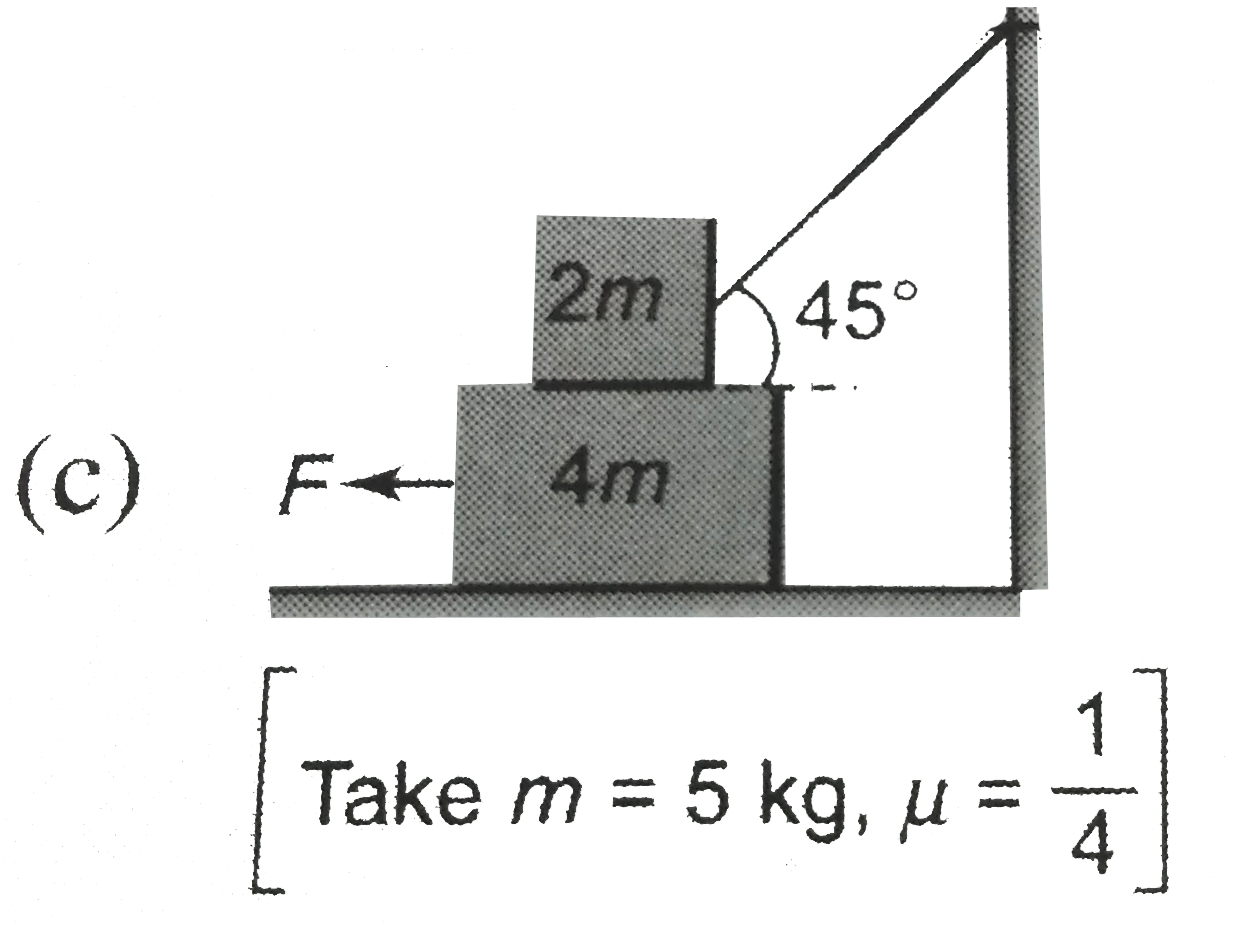
(d)
View SolutionA large rectangular glass block of refractive index μ is lying on a horizontal surface as shown in Figure. Find the minimum value of μ so that the spot S on the surface cannot be seen through top plane ‘ABCD’ of the block.
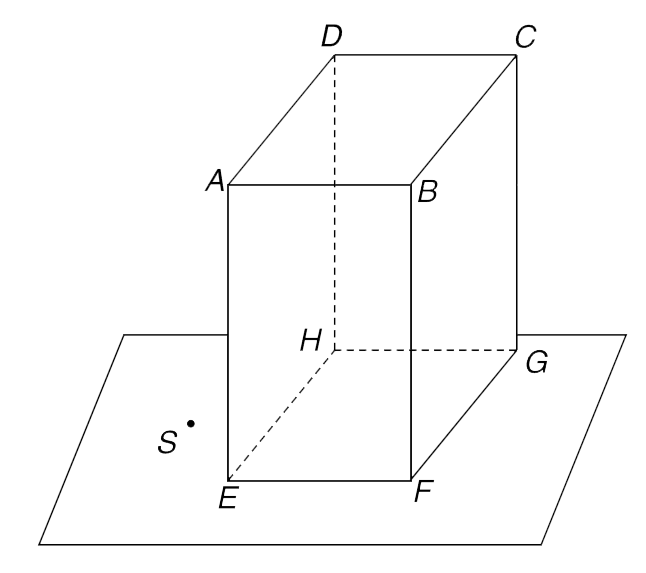View SolutionFind the maximum speed at which a truck can safaly travel without toppling over, on a curve of radius 250m . The height of the centre of gravity of the truck above the ground is 1.5m and the distance between the wheels is 1.5m , the truck being horizontal.
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
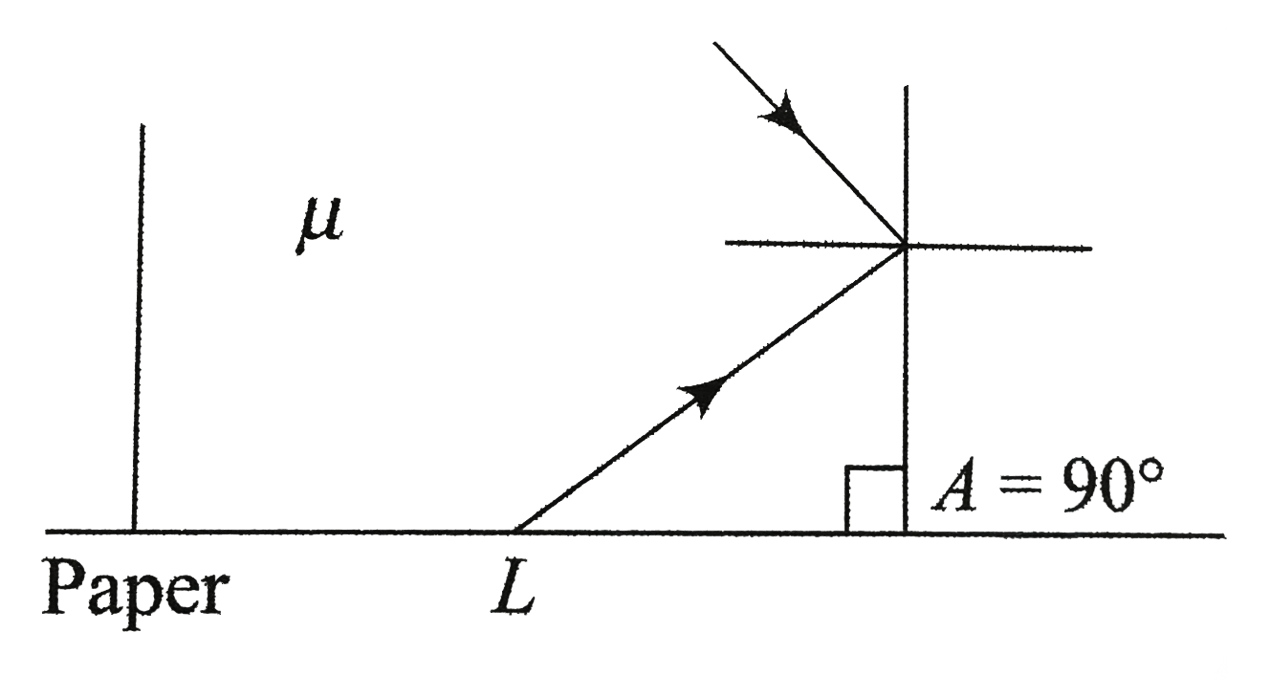View Solution