Find out pressures at point A and B. Also find angle θ. A zig zag tube open at n, having liquis of densities ρ1,ρ2 and ρ3 is placed in a vertical plane as shown in figure. (The pressue at M is equal to atmospheric pressure).

Pressure at A is PA=Patm−ρ1glsinθ
Pressure at B is PB−Patm+ρ2gh
But PB is also given by PB=PA+ρ3glsinθ
Hence Patm+ρ2gh=Pa+ρ3glsinθ
⇒Patm=ρ2gh=Patm−ρ1glsinθ+ρ3glsinθ
⇒sinθ=ρ2h(ρ3−ρ1)l
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A thin triangular glass tube containing immiscible liquids A, B, C of densities ρ,2ρ,3ρ is at rest in vertical plane. Find x.

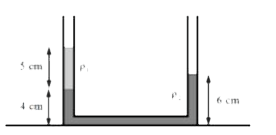
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
View SolutionThree different liquids are filled in a U-tube as shown in figure. Their densities are ρ1,ρ2 and ρ3 respectively. From the figure we may conclude that
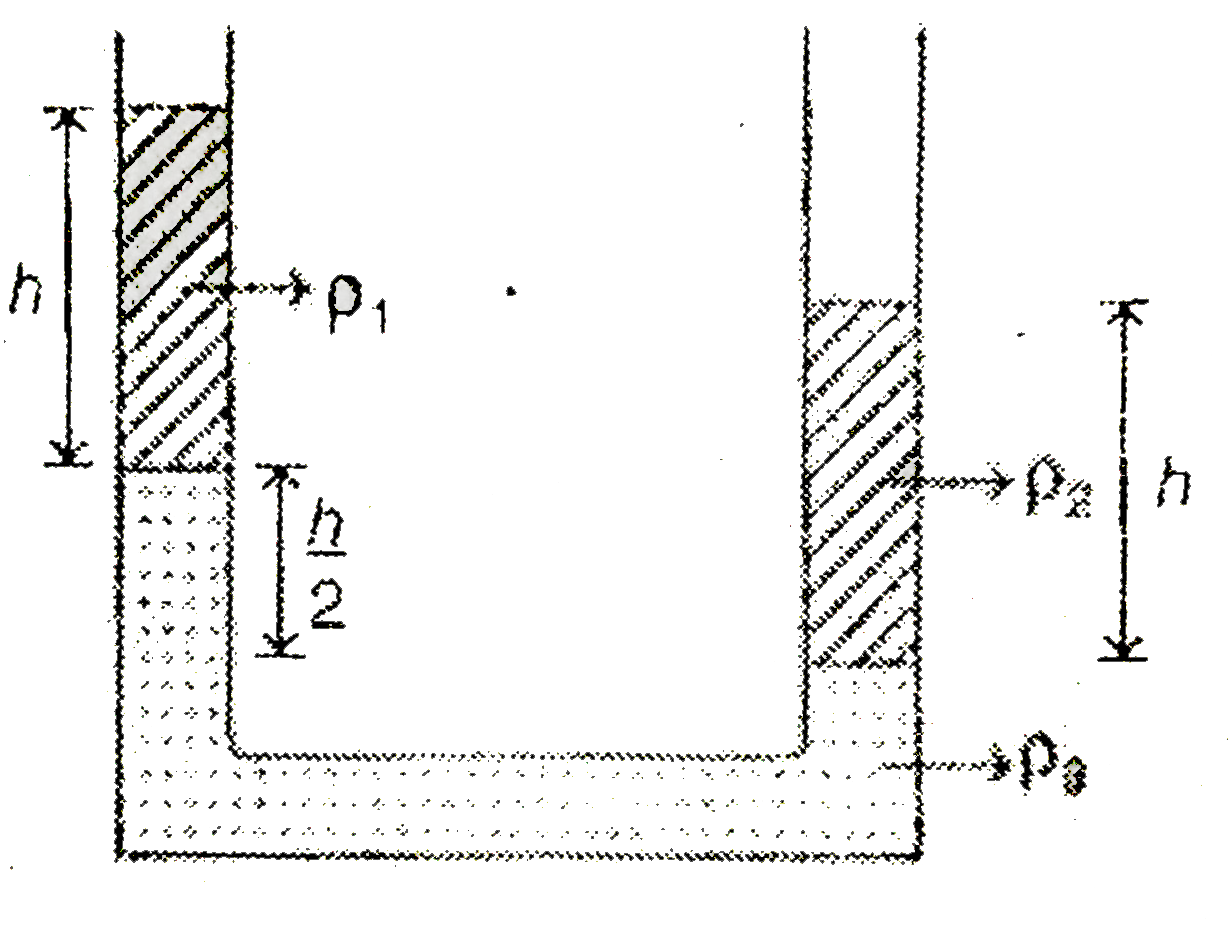
View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionA liquid of density 'ρ' is rotated with an angular speed 'ω' as shown in figure. Using the pressure equation concept find the equation of free surface of the liquid.
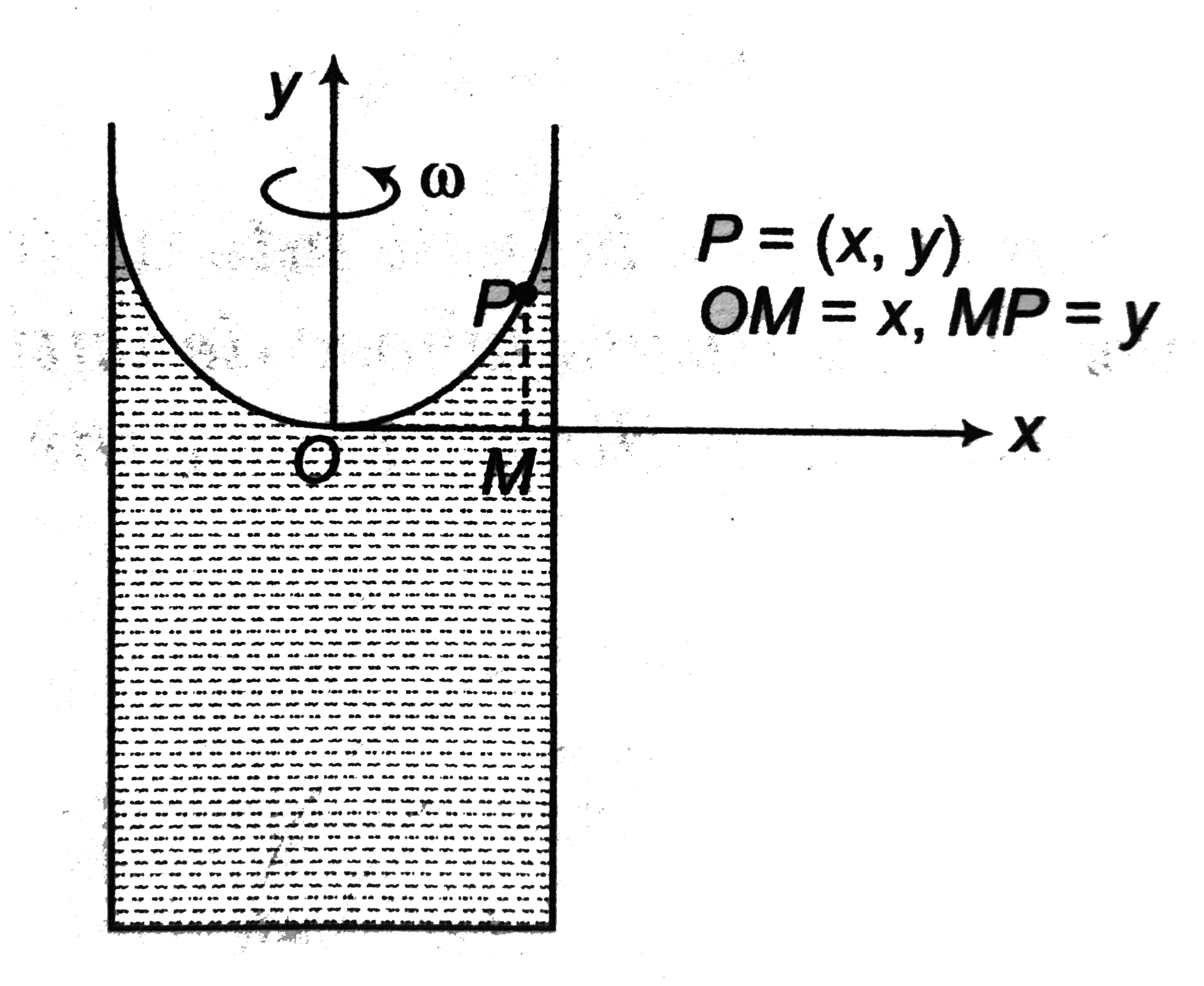 .
.
View SolutionA container A is having some fluid of density θ0. If is connected with a U tube manometer shown in figure. Find the pressure of the container in both the cases given in figure.
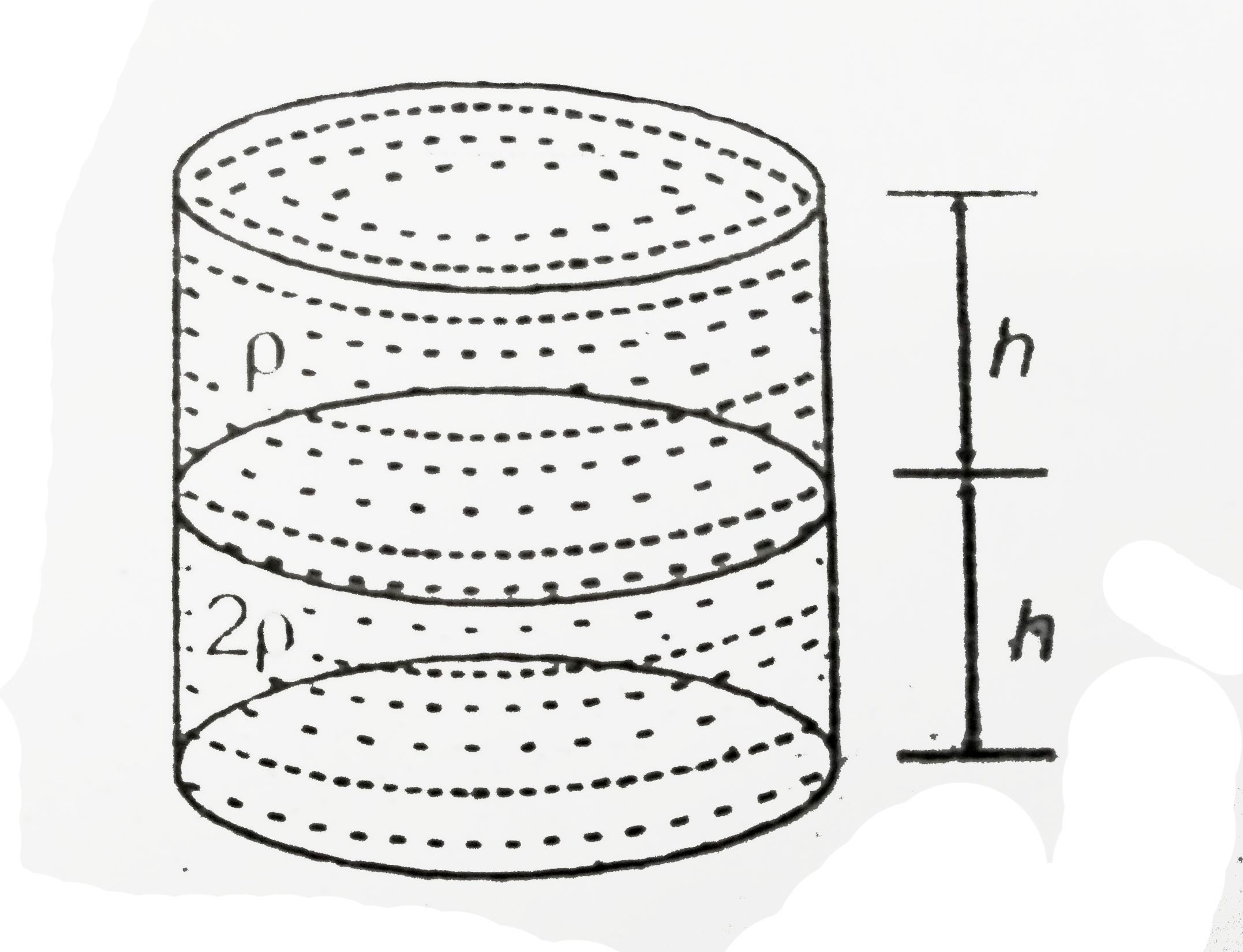
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View Solution
