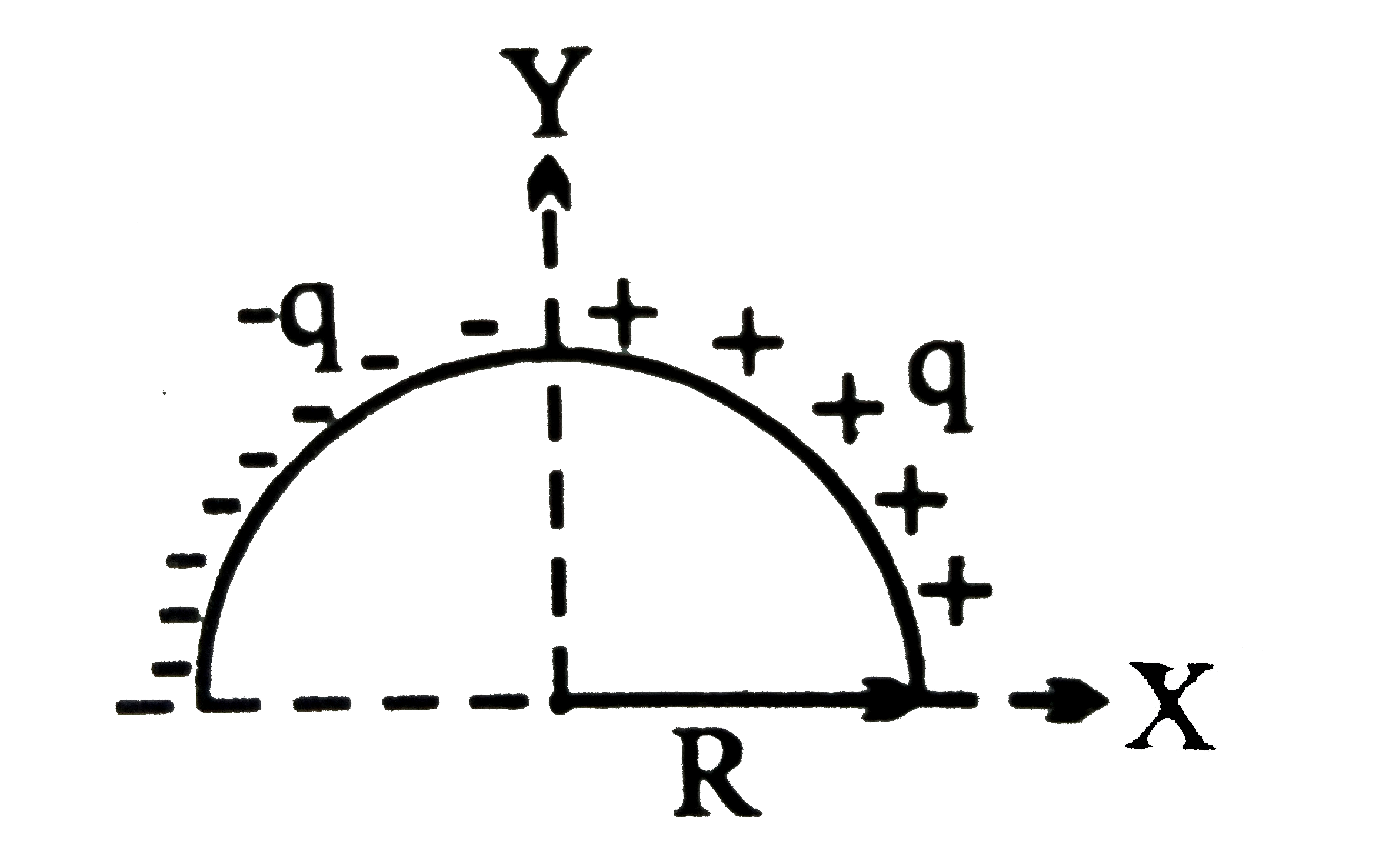
Find the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
λ2πε0a
λ4ε0a
λ2πε0a2
λ24πε0a
The correct Answer is:B
E=∑dQ4πε0a2=∑λdl4πε0a2
∴E=λπa4πε0a2=λ4ε0a
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
Ar−1BrCr2Dr−2 - Question 2 - Select One
The electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπR
In the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
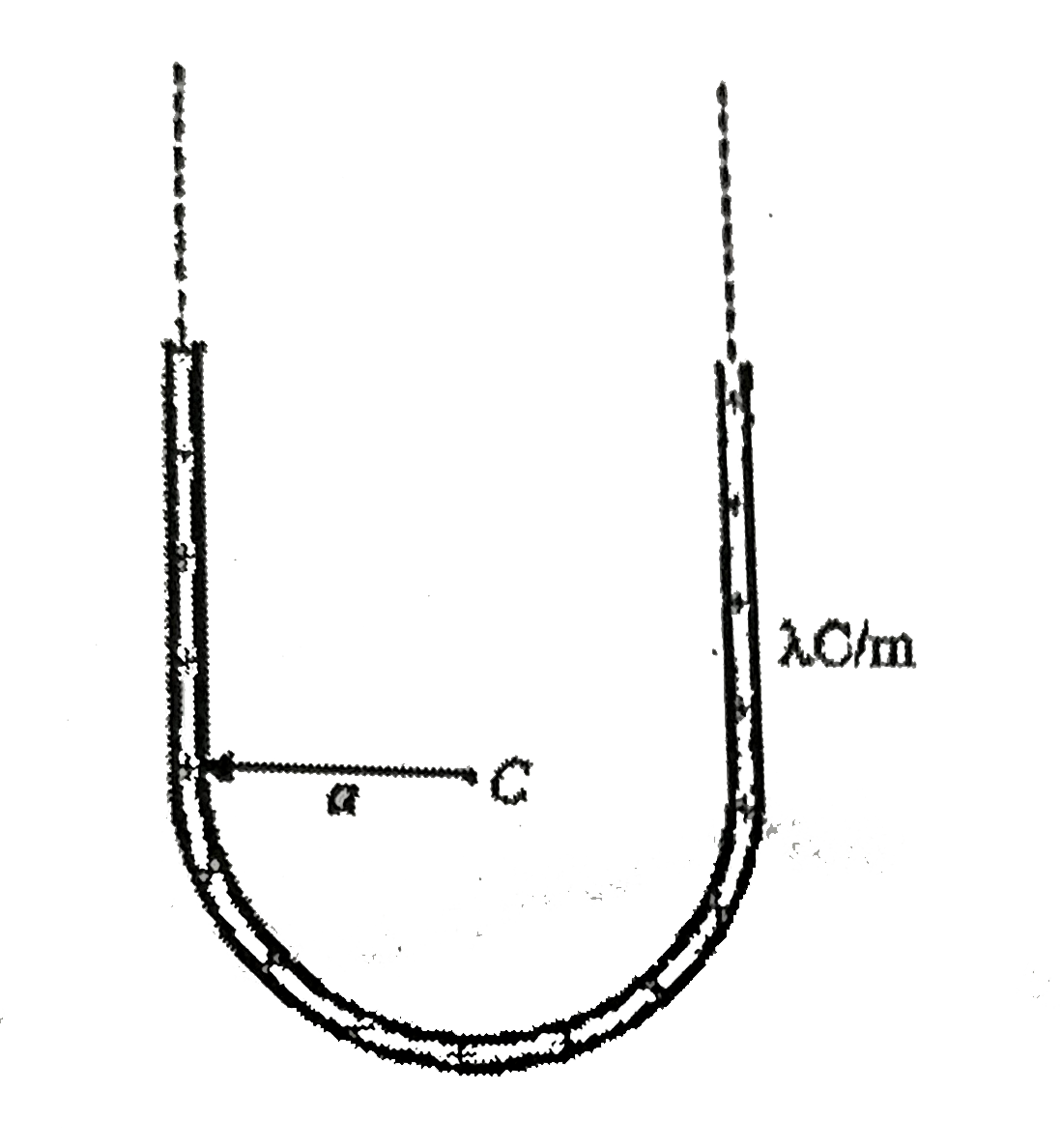 View Solution
View SolutionElectric field at centre O of semicircule of radius 'a' having linear charge density λ given is given by
 View Solution
View SolutionElectric field at the centre of uniformly charge hemispherical shell of surface charge density σ is σnε0 then find the value of n.
 View Solution
View SolutionIf coulomb's law were F=KqQr3, calculate the electric field due to a uniformly charged line charge at a distance d from it. The linear charge density on the line charge is λ C/m, and it is of infinite length.
View SolutionDraw the electric field vs distance (from the centre ) graph for (i) a long charged rod having linear charge density λ>0 (ii) spherical shell of radius R and charge Q>0 .
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View Solution


 .
.