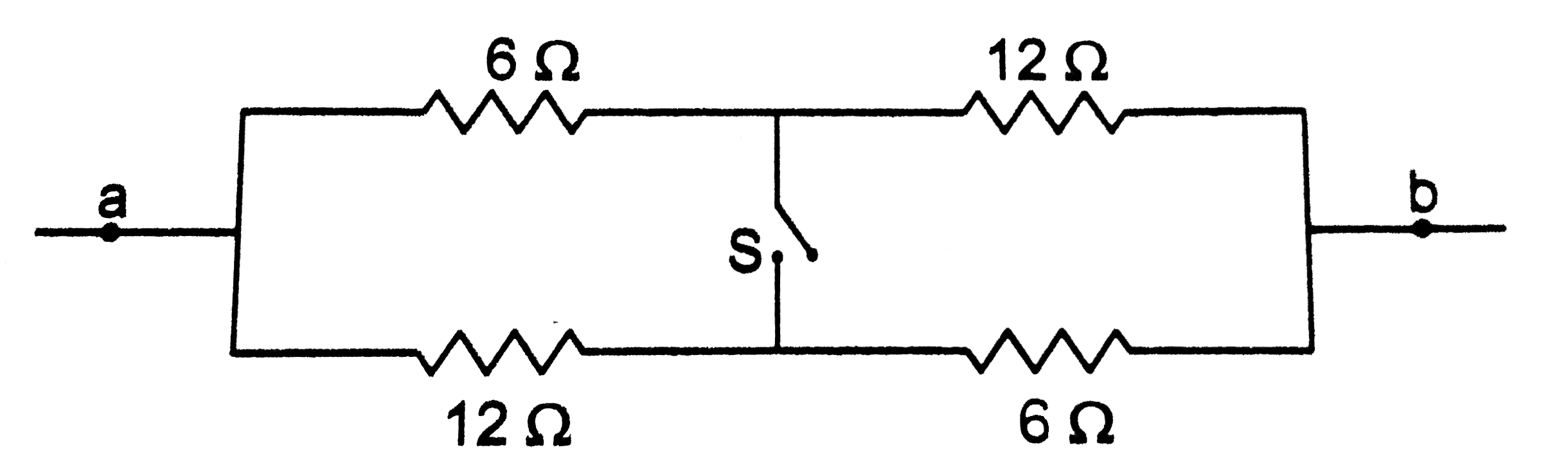
Find the equivalent resistance between the point a and b .
Suppose a current I starts from the positive terminal of the battery. By symmetry,it divides equally in the resistors ab and fe, so that each of these carries a current i2.The current going into the megative terminal is also I and bu symmetry , equal currents should come from ed and bc. Thus, the current in ed is also (i2)and hence there will be no current in eb.
We have,
Va−Vc=(Va−Vb)+(Vb−Vc)
or, 6V=(i2)×10(Ω)+(i2)×10(Ω)
giving i=0.6A.
This is a balanced Wheatstone bridge.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Objective 1
15 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
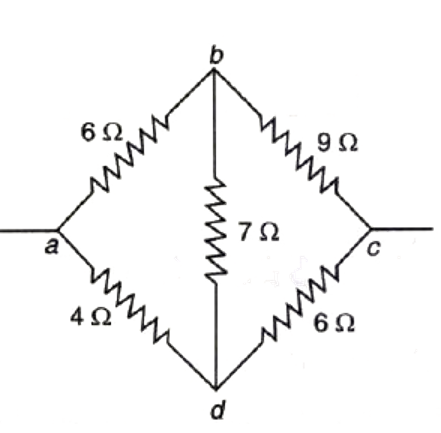
Find the equivalent resistance between the points a and c of the given network for resistors
View SolutionFind the equivalent resistance between thepoints a and b of the infinite ladder shown in figure.

View SolutionFind the equivalent resistances between the points a and c of the network shown in figure. Each resistance is equal to r.
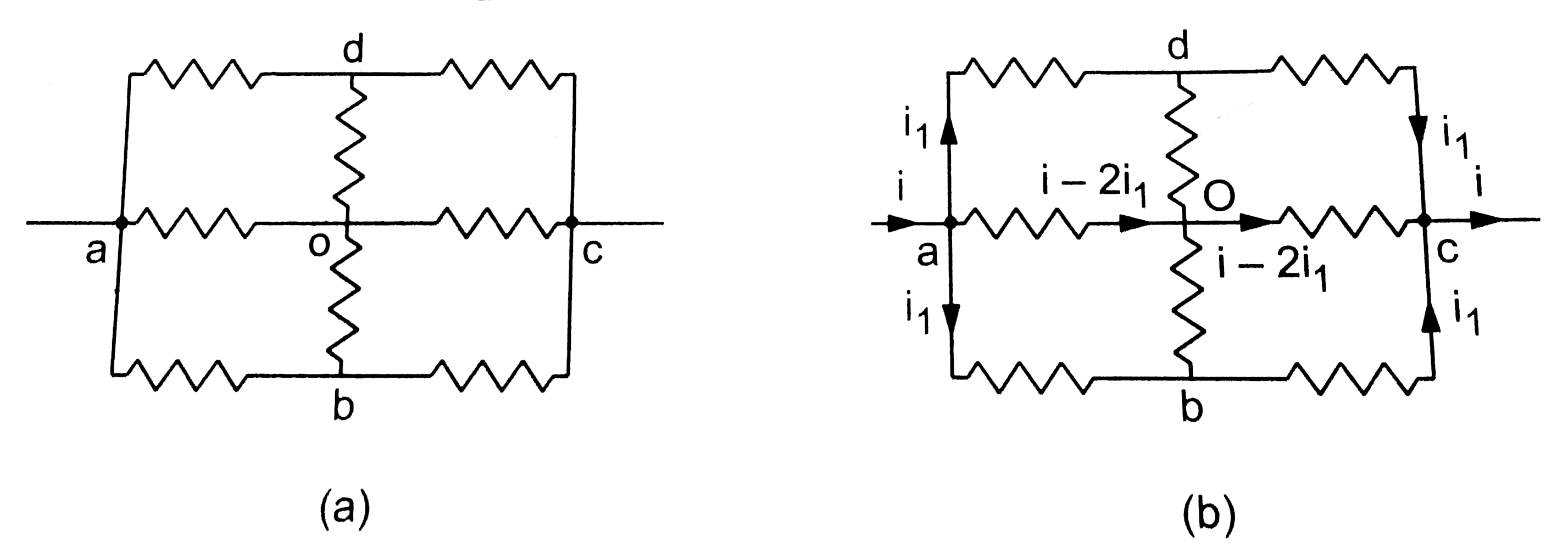
View SolutionFor the combination of resistors shown in Fig. find the equivalent resistance between the points
A and B

View SolutionFind the equivalent resistance between points A and B.
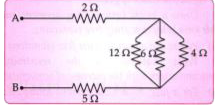
View SolutionFind the equivalent resistance between points A and B.
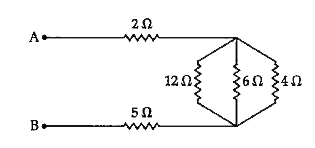
View SolutionFind the equivalent resistance between points A and B

View SolutionWhat is the equivalent resistance between the points A and B of the network?
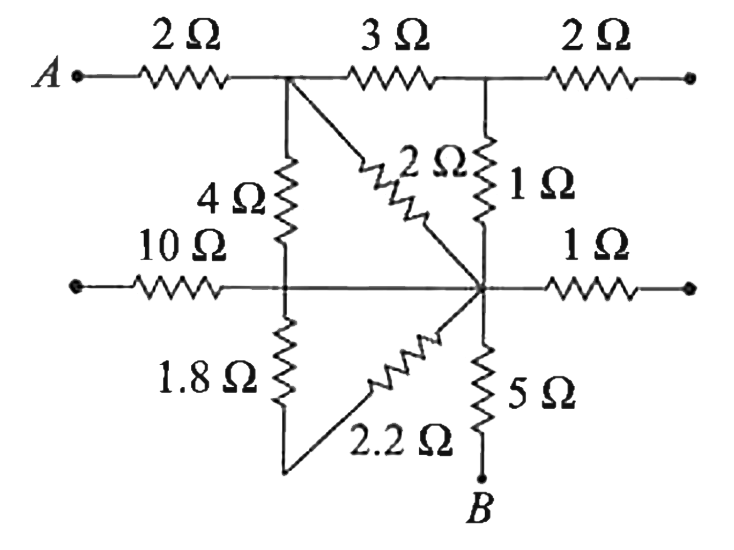
View SolutionThe equivalent resistance between the points A and B is:
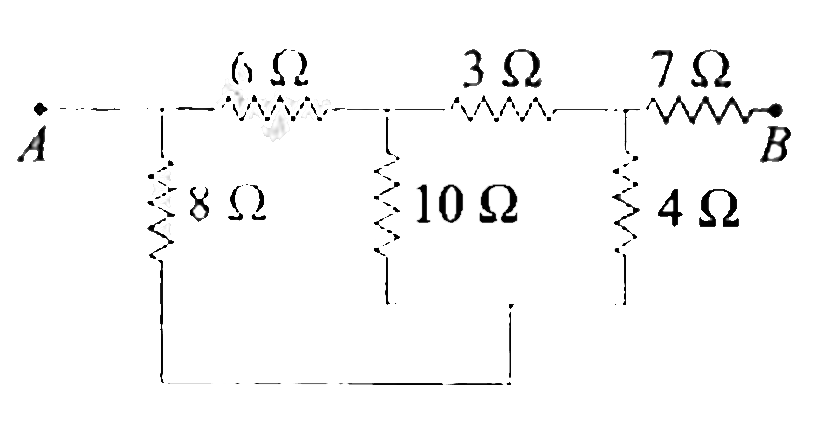
View SolutionFind the the equivalent resistance between points A and B.

View Solution
