Find the minimum and maximum wavelengths of sound in water that is in the audible range (20-20000 Hz) for an average human ear. Speed of sound in water =1450ms−1.
The correct Answer is:B, C
To find the minimum and maximum wavelengths of sound in water that are in the audible range (20 Hz to 20,000 Hz), we can use the formula for wavelength:
λ=Vf
where:
- λ is the wavelength,
- V is the speed of sound in the medium (water in this case),
- f is the frequency.
Given:
- Speed of sound in water, V=1450m/s
- Minimum frequency, fmin=20Hz
- Maximum frequency, fmax=20000Hz
Step 1: Calculate the minimum wavelength
The minimum wavelength occurs at the maximum frequency. Therefore, we use the maximum frequency in our calculation.
λmin=Vfmax
Substituting the values:
λmin=1450m/s20000Hz=145020000=0.0725m=72.5mm
Step 2: Calculate the maximum wavelength
The maximum wavelength occurs at the minimum frequency. Therefore, we use the minimum frequency in our calculation.
λmax=Vfmin
Substituting the values:
λmax=1450m/s20Hz=145020=72.5m
Final Results
- Minimum wavelength λmin=72.5mm
- Maximum wavelength λmax=72.5m
- λ is the wavelength,
- V is the speed of sound in the medium (water in this case),
- f is the frequency.
- Speed of sound in water, V=1450m/s
- Minimum frequency, fmin=20Hz
- Maximum frequency, fmax=20000Hz
The minimum wavelength occurs at the maximum frequency. Therefore, we use the maximum frequency in our calculation.
The maximum wavelength occurs at the minimum frequency. Therefore, we use the minimum frequency in our calculation.
- Minimum wavelength λmin=72.5mm
- Maximum wavelength λmax=72.5m
Topper's Solved these Questions
Similar Questions
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360ms−1.
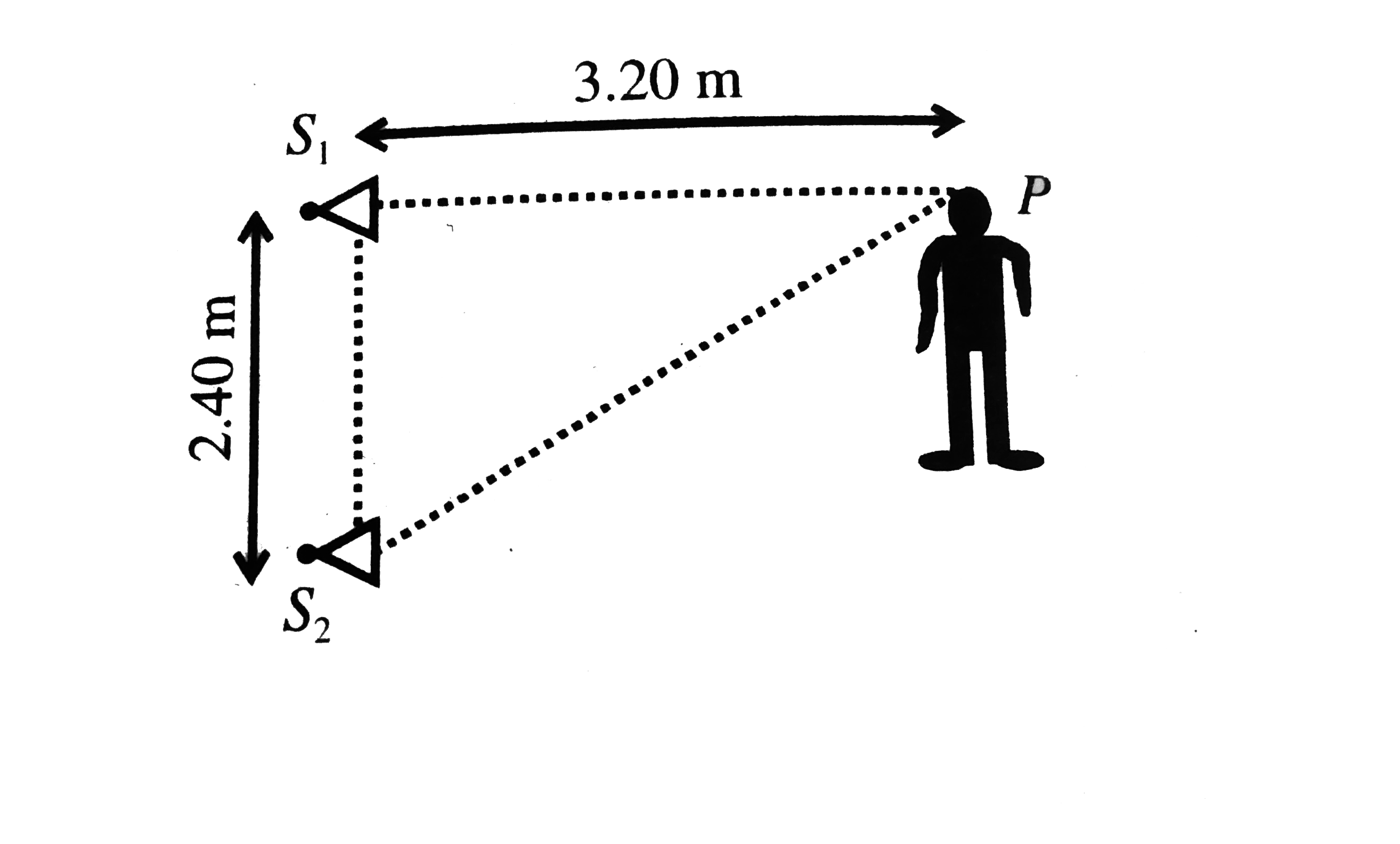
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the bulk modulus of water is 2100 M Pa, what is the speed of sound in water ?
A1450ms−1B2100ms−1C1400ms−1D1200ms−1
A sound wave travelling in water has wavelength 0.4 m.
Is this wave audible in air ? (The speed of sound in water = 1400ms−1)View SolutionTwo stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s.
 View Solution
View SolutionThe minimum wavelength of sound that is audible to a person is (speed of sound is 340 m/s)
View SolutionFind the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20-20,000 Hz). Speed of sound in air =340ms−1.
View SolutionWhat should be the minimum distance between the source and reflector in water so that the echo is heard distinctly ? (The speed of sound in water = 1400 m s−1).
View SolutionA closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air =340ms−1.
View SolutionIn Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340ms−1.
View Solution

