Find the time period of small oscillations of the following systems.
(a) A uniform rod of mass m and length L is suspended through a pin hole at distance from top as shown.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform disc of mass m and radius r suspended through a point away from centre.
(d) A uniform square plate of edge a suspended through a corner.
(a)

Restoring torque about O
(case of SHM)
I: M.I. about OA (OA is to plane of motion)
(b) 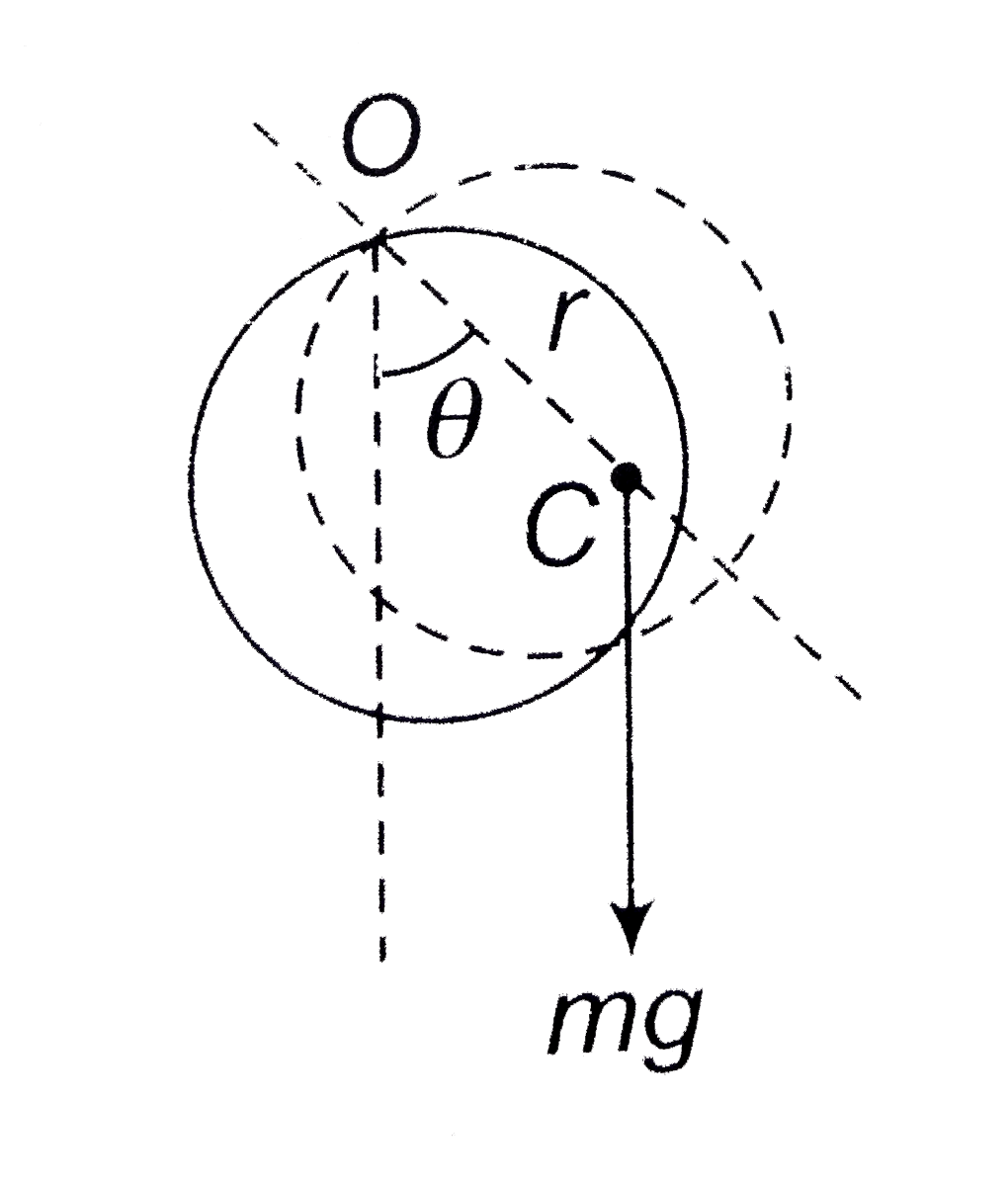
(c) 
,
()
,
(d) 
()
Topper's Solved these Questions
Similar Questions
Find the time period of small oscillations of the following system. a. A metre stick suspended through the 20 cm mark. b. A ring of mas m and radius r suspended through a pointon it speriphery. c. A uniform sdquare plate of edge a suspended through a corner. d. A uniform disc of mass m and radius r suspended through a point r2 away from the centre.
View SolutionCompound pendulum are made of :
(a) A rod of length l suspended through a point located at distance l/4 from centre of rod.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform square plate of edge a suspended through a corner.
(d) A uniform disc of mass m and radius r suspeneded through a point r/2 away from the centre.
Find the time period in each case.View Solution
Knowledge Check
- Question 1 - Select One
Find time period of uniform disc of mass m and radius r suspended through point r/2 away from centre, oscillating in a plane parallel to its plane.
A2π√2r3gB4π√r2gC2π√3r2gDNone of these - Question 2 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR - Question 3 - Select One
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3g
Find the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.
 View Solution
View SolutionA disc of mass 'm' is suspended at a point R/2 above its centre. Find its period of oscillation.
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its one end will be
View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View SolutionThe radius of gyration of a uniform disc of radius R, about an axis passing through a point R2 away from the centre of disc, and perpendicular to the plane of disc is:
View Solution

