Find total internal energy of 3 moles of hydrogen gas at temperature .
The correct Answer is:B, C
To find the total internal energy of 3 moles of hydrogen gas at temperature T, we can follow these steps:
1. Identify the Formula for Internal Energy:
The internal energy U of an ideal gas can be expressed as:
U=nCVT
where:
- n = number of moles,
- CV = molar heat capacity at constant volume,
- T = temperature.
2. Determine the Number of Moles:
From the problem, we know:
n=3 moles
3. Identify the Type of Gas:
The gas in question is hydrogen (H2), which is a diatomic gas.
4. Calculate the Degrees of Freedom:
For a diatomic gas, the degrees of freedom F is given by:
F=5
(3 translational + 2 rotational).
5. Calculate CV:
The molar heat capacity at constant volume CV for a diatomic gas is given by:
CV=F2R=52R
where R is the universal gas constant.
6. Substitute CV into the Internal Energy Formula:
Now, substituting CV into the internal energy formula:
U=nCVT=n(52R)T
7. Insert the Value of n:
Substituting n=3:
U=3(52R)T
8. Simplify the Expression:
U=152RT
9. Final Result:
Thus, the total internal energy of 3 moles of hydrogen gas at temperature T is:
U=152RT
The internal energy U of an ideal gas can be expressed as:
U=nCVT
where:
- n = number of moles,
- CV = molar heat capacity at constant volume,
- T = temperature.
From the problem, we know:
n=3 moles
The gas in question is hydrogen (H2), which is a diatomic gas.
For a diatomic gas, the degrees of freedom F is given by:
F=5
(3 translational + 2 rotational).
The molar heat capacity at constant volume CV for a diatomic gas is given by:
CV=F2R=52R
where R is the universal gas constant.
Now, substituting CV into the internal energy formula:
U=nCVT=n(52R)T
Substituting n=3:
U=3(52R)T
U=152RT
Thus, the total internal energy of 3 moles of hydrogen gas at temperature T is:
U=152RT
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Example Type 1
1 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Example Type 2
1 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
Internal energy of n moles of helium at temperature T1K is equal to the internal energy of 2n moles of oxygen gas at temperature T2K then the value of T1T2will be
View SolutionThe internal energy of one mole of ideal gas is
View Solution
Consider a gas of triatomic molecules. The molecules are assumed to be triangular and made of massless rigid rods whose vertices are occupied by atoms. The internal energy of a mole of the gas at temperature T is:
View SolutionThe average value of rotational kinetic energy of one mole of oxygen gas at temperature T will be
View SolutionInternal energy of n1 moles of hydrogen at temperature 150 K is equal to the in ternal energy of n2 moles of helium at temperature 300 K The ratio of n1/n2 is
View SolutionInternal energy of n1 mol of hydrogen of temperature T is equal to the internal energy of n2 mol of helium at temperature 2T. The ratio n1/n2 is
View SolutionAssertion Total internal energy of oxygen gas at a given temperature is E of this energy 35 E is rotational kinetic energy.
Reason Potantial energy of an ideal gas is zero.
View SolutionConsider a P−V diagram in which the path followed by one mole of perfect gas in a cyclinderical container is shown in (figure)
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperatures T1/T2,ifV2=2V1?
(c ) Given the internal energy for one mole of gas at temperature Tis(3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2=2V1.
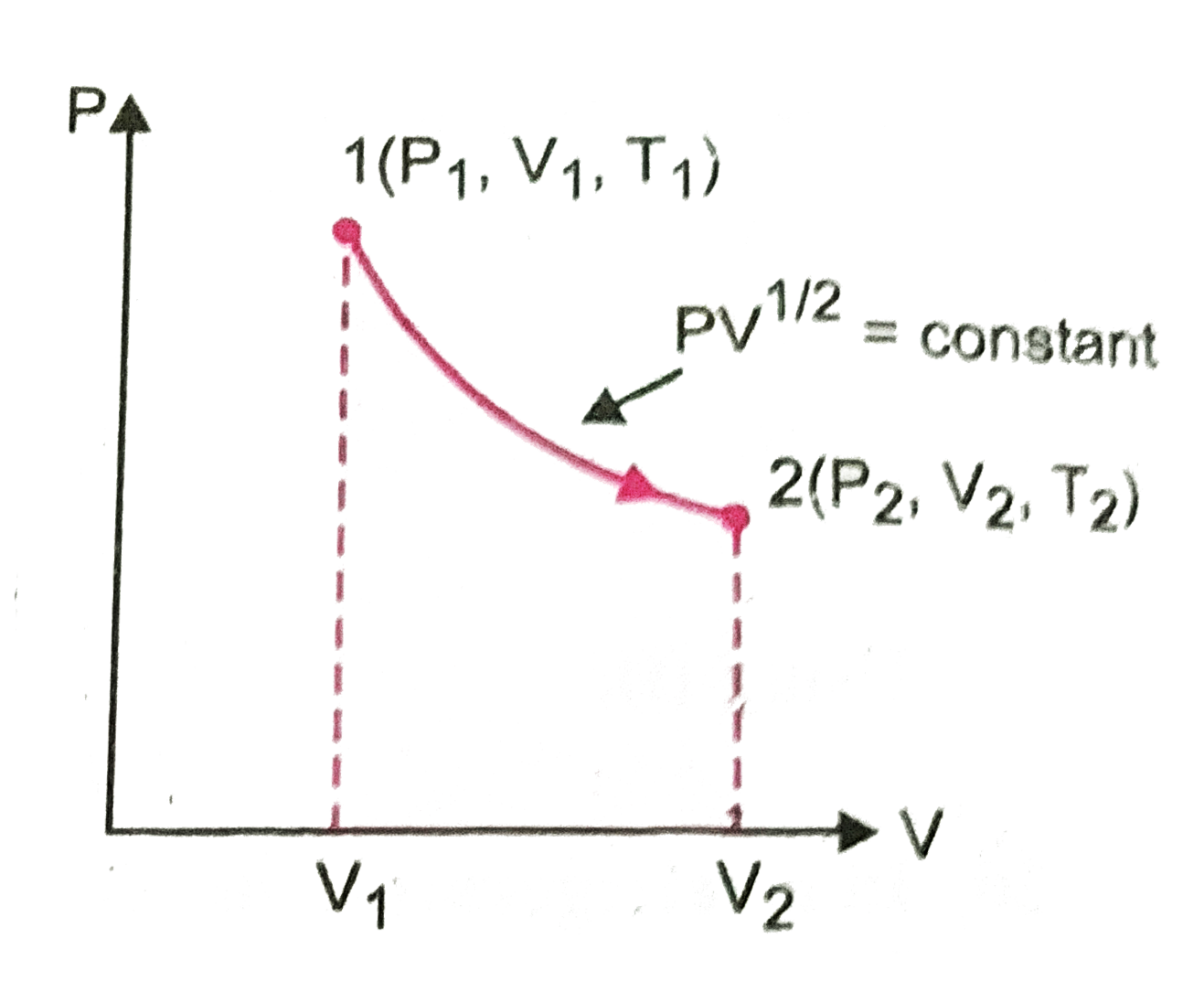
View SolutionCalculate the change in internal energy of 3.0 mol of helium gas when its temperature is increased by 2.0K.
View Solution(a) What is the average translational kinetic energy of a molecule of an ideal gas at temperature of 276∘C ?
(a) What is the total random translational kinetic energy of the molecules in one mole of this gas ?
( c) What is the rms speed of oxygen molecules at this temperature ?
View Solution
