Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
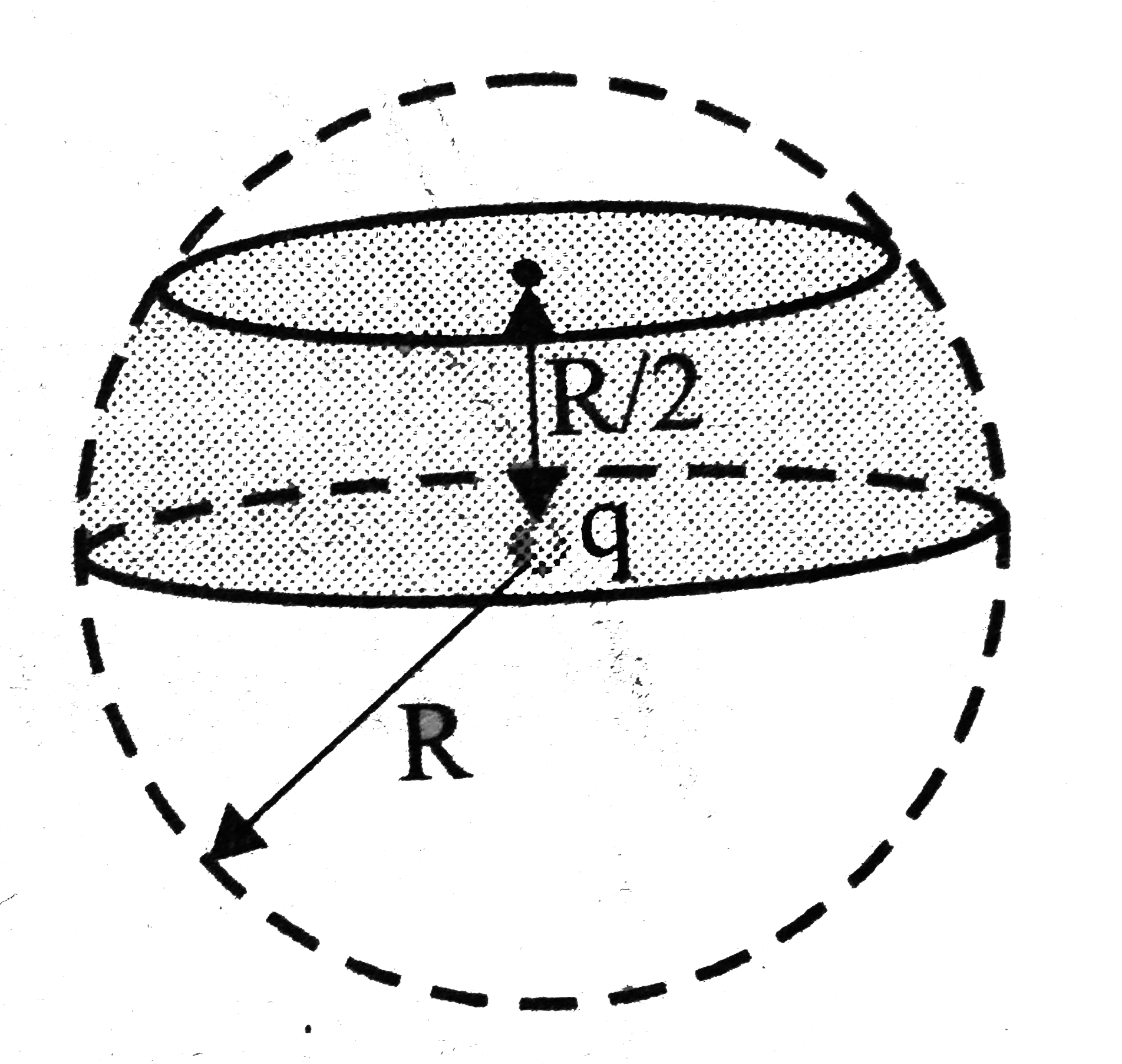
qε0
q2ε0
q4ε0
zero
The correct Answer is:C
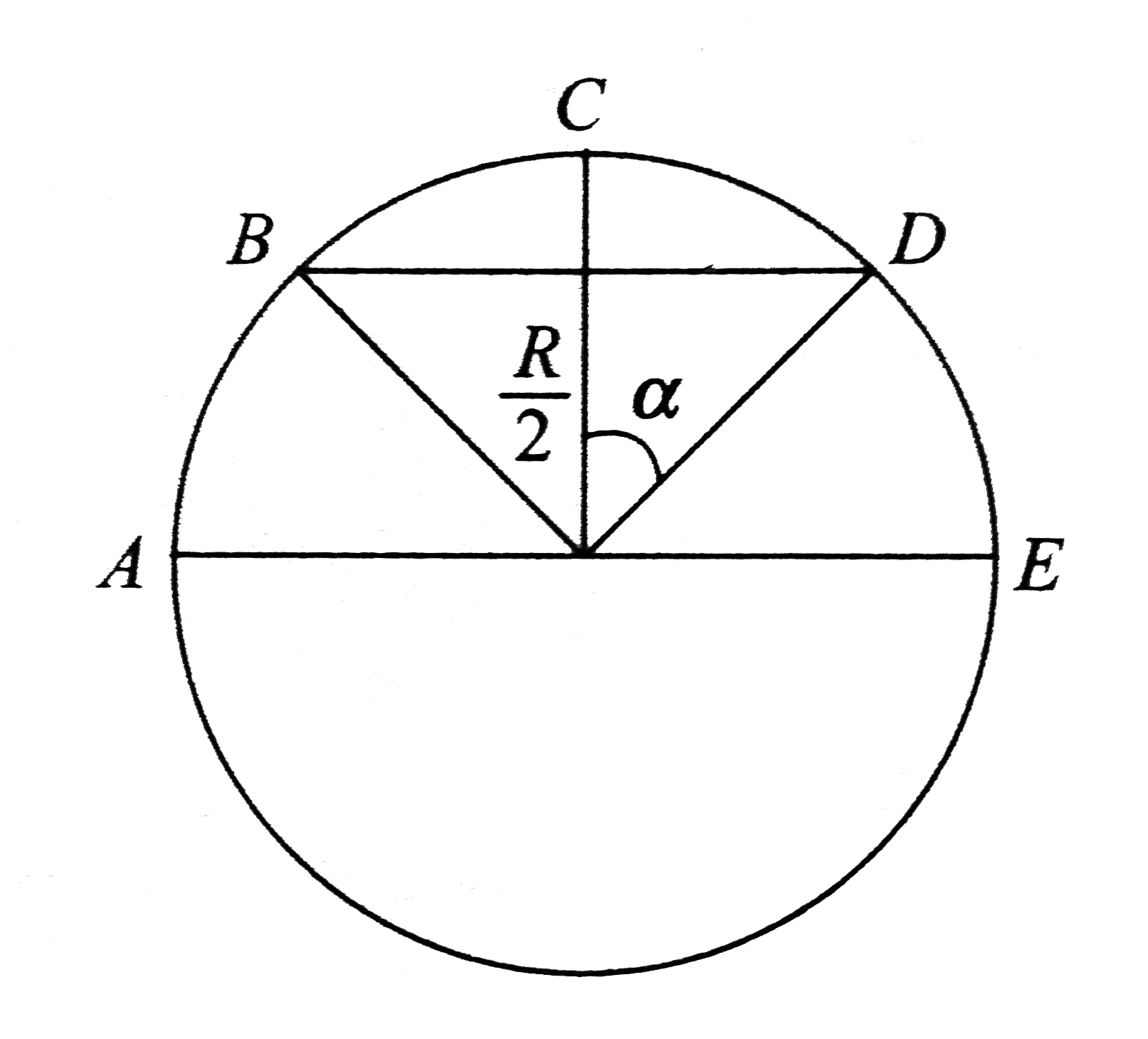
c. α=60∘. Solid angle subtended by BCD is
ω=2π(1−cosα)=π
Solid angle subtended by ABDE is
ωABCDE−ωBCD=2π−π=π
Hence, flux through ABDE is
ϕ=qε0π4π=q4ε0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.514videos
ELECTRIC POTENTIAL
Similar Questions
A hollow conducting sphere of inner radius r1 and outer radius r2 has a charge Q on its surface. A point charge - q is also placed at the centre of the sphere .
(a) What is the surface charge density on the (i) inner and (ii) outer surface of the sphere ?
(b) Use Gauss' law of electrostatics to obtain the expression for the electric field at a point lying outside the sphere.View SolutionWhen a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View Solution
Knowledge Check
- Question 1 - Select One
A solid, uncharged conducting sphere of radius 3a contains a concentric hollowed spherical cavitiy of radius a.
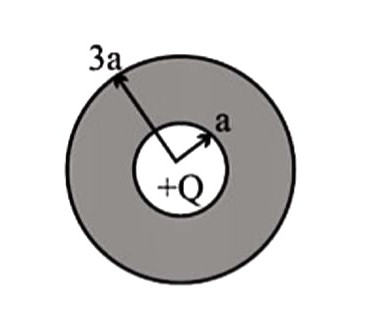
A point charge +Q is placed at the center of the spheres. Taking V=0 at r→∞, the potential at positiion r=2a from the center is-AKQaBKQ2aCKQ3aD2KQ3a - Question 2 - Select One
A hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is
 Aμ0qω2πRBμ0qω3πRCμ0qω6πRDμ0qω12πR
Aμ0qω2πRBμ0qω3πRCμ0qω6πRDμ0qω12πR - Question 3 - Select One
Charge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
AϕB34πϕC2π3ϕD4π3 phi
Charge is distributed uniformly in some space. The net flux passing through the surface of an imaginary cube of side a in the space is ϕ. The net flux passing through the surface of an imaginary sphere of radius a in the space will be
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
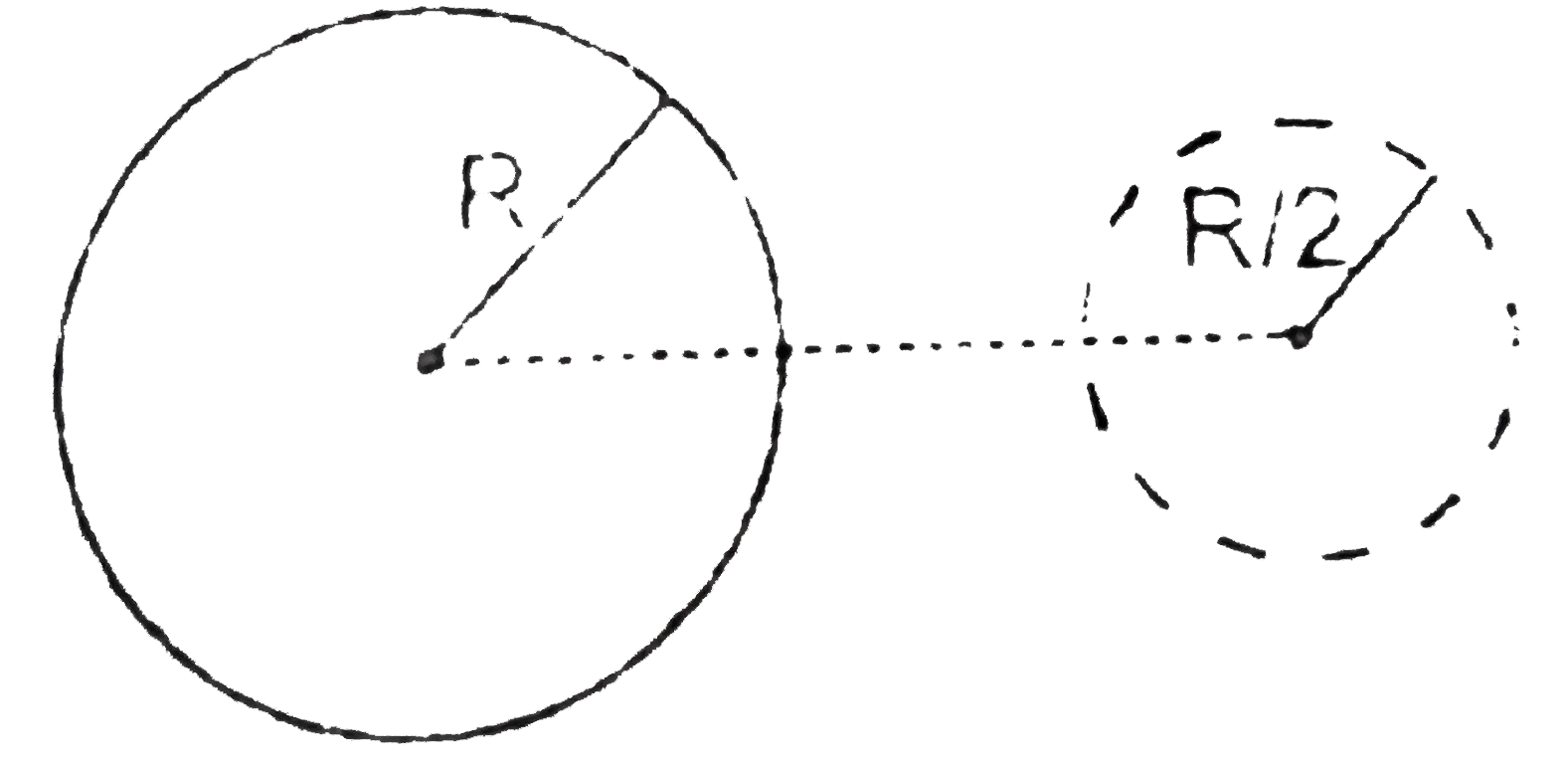 View Solution
View SolutionA charged particle is suspended at the centre of two thin concentric spherical charged shells, made of non conducting material. Figure A shows cross section of the arrangement. Figure B gives the net flux ϕ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.

What is the charge on shell A ?View SolutionA charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux ϕ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
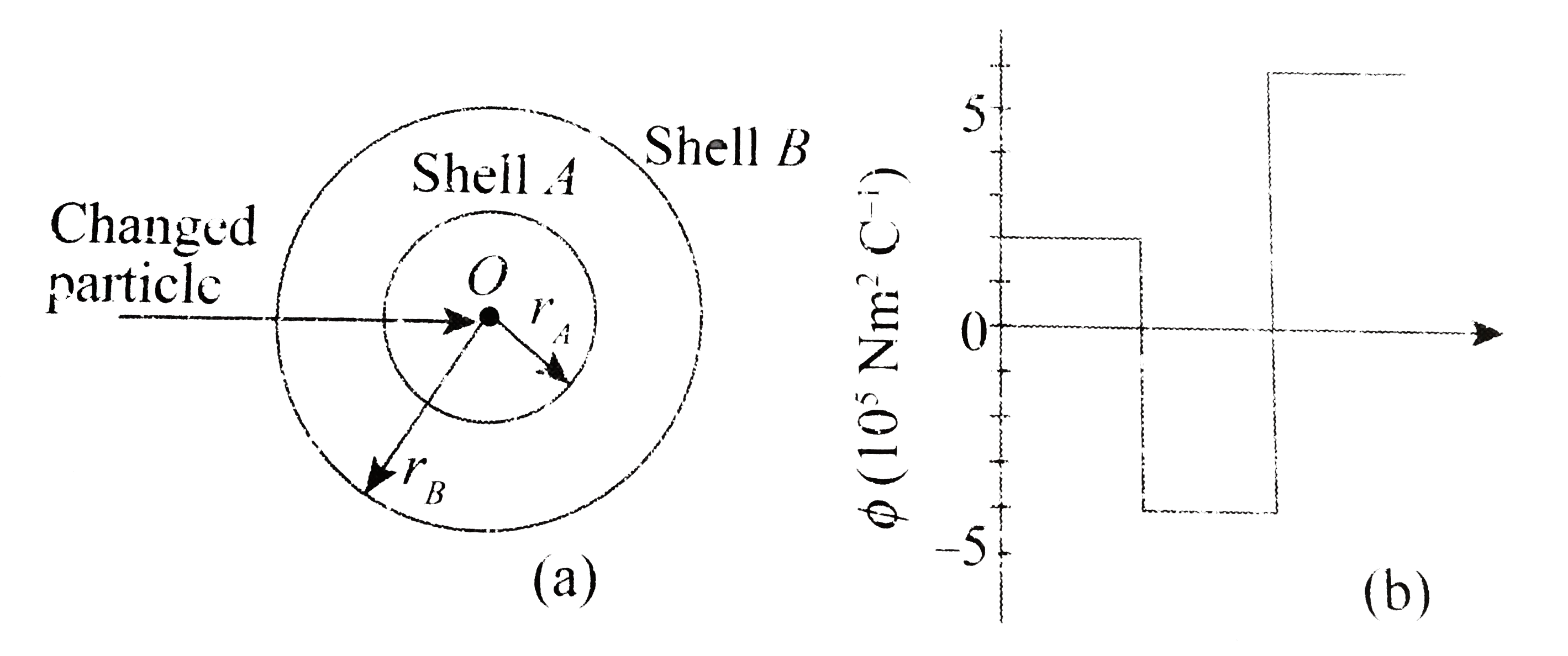 ,
,
What is the charge on the central particle?View SolutionThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
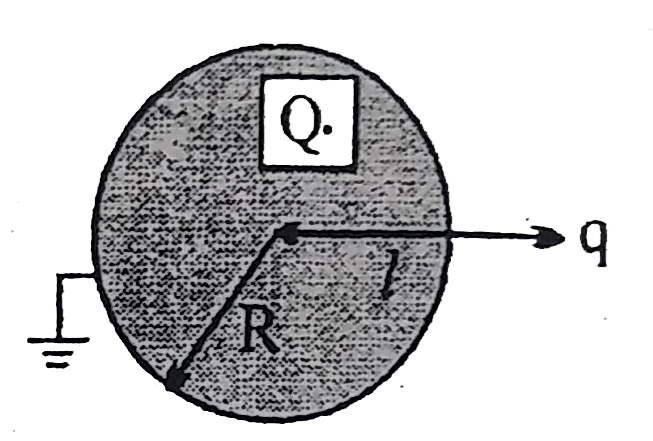
Net charge on the outer surface of conducting sphere isView Solution

