For steel the Young modulus of elasticity is 2.9×1011Nm−2 and density is 8×103kgm−3. Find the velocity of the longitudinal waves in steel.
To find the velocity of longitudinal waves in steel, we can use the formula:
v=√Eρ
where:
- v is the velocity of the longitudinal wave,
- E is the Young's modulus of elasticity,
- ρ is the density of the material.
Step 1: Identify the given values
From the problem, we have:
- Young's modulus of elasticity E=2.9×1011N/m2
- Density ρ=8×103kg/m3
Step 2: Substitute the values into the formula
Now, we can substitute the values of E and ρ into the formula for the velocity of longitudinal waves:
v=√2.9×10118×103
Step 3: Calculate the value inside the square root
First, we need to calculate the fraction:
2.9×10118×103=2.98×1011−3=0.3625×108
Step 4: Take the square root
Now, we take the square root of the result:
v=√0.3625×108=√0.3625×104
Calculating √0.3625:
√0.3625≈0.6021
Thus,
v≈0.6021×104m/s
Step 5: Convert to standard form
This can be written as:
v≈6021m/s
Final Answer
The velocity of the longitudinal waves in steel is approximately:
v≈6020m/s
---
- v is the velocity of the longitudinal wave,
- E is the Young's modulus of elasticity,
- ρ is the density of the material.
From the problem, we have:
- Young's modulus of elasticity E=2.9×1011N/m2
- Density ρ=8×103kg/m3
Now, we can substitute the values of E and ρ into the formula for the velocity of longitudinal waves:
First, we need to calculate the fraction:
Now, we take the square root of the result:
This can be written as:
The velocity of the longitudinal waves in steel is approximately:
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-D (Answer the following )6videos
SELF ASSESSMENT PAPER 02
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-B (Answer the following )13videos
SELF ASSESSMENT PAPER 02
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECION- D (Answer the following )6videos
SELF ASSESSMENT PAPER 01
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 3
Similar Questions
Young 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionA steel rod of length l1=30cm and two identical brass rod of length l2=20cm each support a light horizontal platform as shown in Fig. Cross-sectional area of each of the three rods is A=1cm2. A vertically downward force F=5000N is applied on the platform. Young's modulus of elasticity for steel Ys=2×1011Nm−2 and brass Yb=1×1011Nm−2. Find stress (in MPa) developed in a. Steel rod b. Brass rod
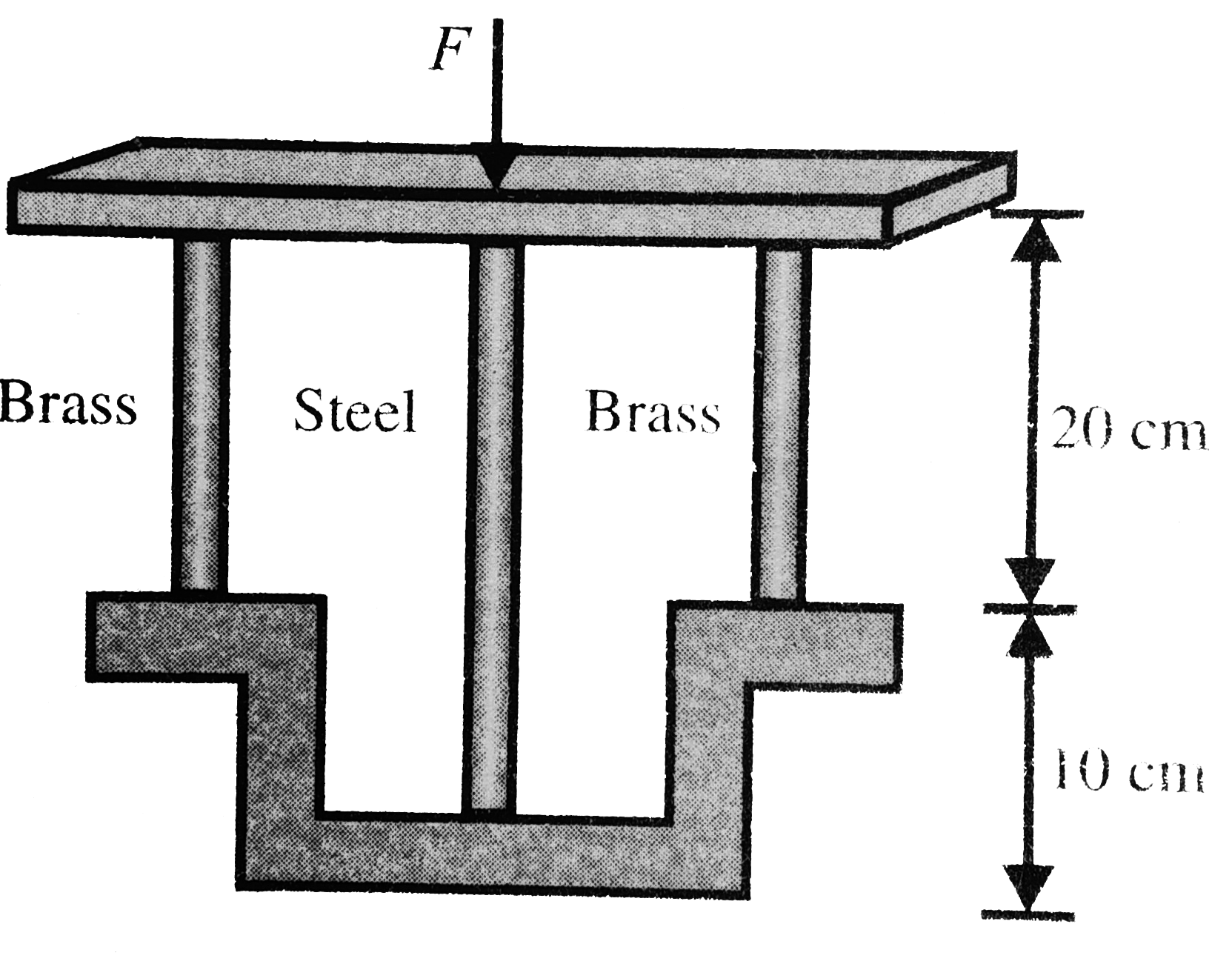 View Solution
View SolutionFor aluminium the bulk modulus and modulus of rigidity are 7.5×1010Nm−2. Find the velocity of longitudinal waves in the medium. Density of aluminium is 2.7×103kgm3.
View SolutionThe Youngg's modulus of a material is 6×1010Nm−2 and its bulk modulus is 2.8×1010Nm−2 . What is its Poisson's ratio ?
View SolutionFor brass, bulk modulus and modulus of rigidity are 10.72×1010Nm−2 and 3.6×1010Nm−2. If the density of brass is 8.4×103kgm−3, find the speed of longitudinal and transverse waves in it.
View SolutionThe Young's modulus of brass is 9.1×1010N/m2and its rigidity modulus is 3.5×1010N/m2. Calculate its Poisson's ratio ?
View SolutionA steel rod 2.5m long is rigidly clamped at its centre C and longitudinal waves are set up on both sides of C by rubbing along the rod . Young's modulus for steel =2×1011N/m2 , density of steel =8000kg/m3

If the clamp of the rod be shifted to its end A and totally four antinodes are observed in the rod when longitudinal waves are set up in it , the frequency of vibration of the rod in this mode isView SolutionThe density of aluminium is 2.7×103kg/m3 and its Young's modulus is 7.0×1010N/m2. Calculate the velocity of sound wave in the bar.
View SolutionA metallic rod of length 1 m, young's modulus 3×1011Nm−3 and density is 7.5×102kgm3clamped at its middle. Longitudinal stationary vibrations are produced in the rod with the total number of displacement nodes equal to 3. The frequency of vibrations is
View SolutionCalculate the Poisson's ratio for steel. Given that Young's modulus is 2×1011Nm−2 and rigidity modulus is 8×1010Nm−2.
View Solution

