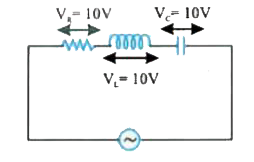
For the L-R-C series circuit described in the above Illustration 5.7, describe the time dependence of the instantaneous current and each instantaneous voltage.
we found the amplitude of the current and voltages. Now we have to find the expressions for the instantaneous values of the current and voltages. As we learned, the voltage across a resistor is in phases with the current but the voltages across an inductor or capacitor are not. We also learned in this section that ϕ is the phase angle between the source voltage and the current.
The current and all the voltage oscillate with the same angular frequency.
Let us choose
E=E0sinωt⇒E=50sin(10,000t)
then II_(0)sin(10,000t+ϕ),
where ϕ=−53∘=−53×π180rad=−0.93rad
⇒I=0.10sin(10,000t−0.93)
Current and voltage are in phase in resistor so
VR=VR0sin(10,000t−0.93)=30sin(10,000t−0.93)
In inductor voltage voltage leads current by π/2 so ,
VL=VL0sin[10,000t−0.93+(π/2)]=60cos(10,000t−0.93)
In capcitor voltage lags currents lags currents by (π/2) so
VC=VC0sin[10,000t−0.93+(π/2)]
=−20cos(10,000t−0.93).
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Solved Examples
6 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.1
15 Videos
- OSCILLATIONSBOOK - CENGAGE PHYSICSCHAPTER - OSCILLATIONSEXERCISE - QUESTION BANK
39 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
Knowledge Check
In L−C−R series circuit
Acurrent may achieve same value for two different value of frequencyBcurrent can not achieve same value for two different values of frequencyCcurrent is maximum for a maximum value of frequencyDnone of theseIn a.c. circuit, the instantaneous value of e.m.f. and current are
A100 WB75 WC50 WD25 WIn an AC series circuit, the instanctaneous current is zero when the instantaneous voltage is xamimum. Connected to the source may be a
Apure inductorBpure capacitorCpure resistorDcombination of an inductor and a capacitor
A series L-C-R circuit is given in figure . The current through the circuit is
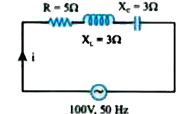
View SolutionThe series L–C–R circuit shown in fig. is in resonance state. What is the voltage across the inductor?
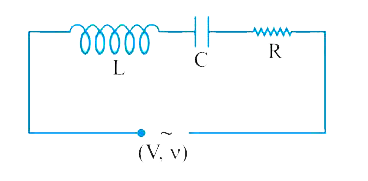
View SolutionDraw phase diagram for a series LCR circuit with alternating voltage source, determine the expression for the impedance of the circuit.
OR
Draw a diagram of AC generator and describe it.Derive an expression for instantaneous value of induced emf.
View SolutionIn a circuit an a.c. current and a d, c. current are supplied together. The expression of the instantaneous current is given as i=3+6sinωt Then the rms value of the current is –
View SolutionAssertion : In series L−C−R,AC circuit, current and voltage are in same phase at resonance.
Reason : In series L−C−R,AC circuit, resonant frequency does not depend on the value of resistance. Hence, current at resonance does not depend on resistance.
View Solution