For the one dimensional motion, described by x=t−sint
x(t)>0 for all t>0
v(t)>0 for all t>0
a(t)>0 for all t>0
v(t) lies between 0 and 2
The correct Answer is:A, D
Given, x=t−sint
velocity v=dxdt=ddt[t−sint]
=1−cost
Acceleration a=dvdt=ddt[1−cost]=sint
As acceleration a>0 for all t>0
Hence, x(t)>0 for all t>0
Velocity v=1−cost
when, cost=1,velocityv=0
vmax=1−(cost)min=1−(−1)=2
vmin=1−(cost)max=1−1=0
Hence, v lies between 0 and 2
Acceleration a=dvdt=−sint
When , t=0,x=0,x=+1,a=0
When, t=π2,x=1,v=0,a=−1
When t=π,x=0,x=−1,a=1
When t=2π,x=0,x=0,a=0
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns
14 Videos
- MOTION IN A STRAIGHT LINE BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns
14 Videos
- MOTION IN A PLANEBOOK - NCERT EXEMPLARCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions
37 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
Similar Questions
The motion of a particle executing SHM in one dimension is described by x=−0.5sin(2t+π/4) where x is in meters and t in seconds. The frequency of oscillation in Hz is
View SolutionFor a particle in one dimensional motion, the instantaeous speed is always equal to the magnitude of instantaneous velocity. Why ?
View Solution
Knowledge Check
Force on a particle in one-dimensional motion is given by F=Av+Bt+CxAt+D, where F= force, v= speed, t= time, x= position and A, B, C and D are constants. Dimension of C will be-
AM2L−2T0BML−1T0CM2L0T−2DNone of theseIn the one-dimensional motion of a particle, the relation between position x and time t is given by x2+2x=t (here x>0). Choose the correct statement.
AThe retardation of the particle is 14(x+1)3BThe uniform velocity of the particle is 1(x+1)3CBoth are correctDBoth are wrongIn one dimensional motion, instantaneous speed y satisfies the condition 0 −VoT<x<voT
3) the acceleration is always a 1 - negative number 4) the motion has no turning pointsAthe displacement in time T must always take non- negative valuesBthe displacement in time T satistics : −v0T<x<v0TCthe acceleration is always a non - negative numberDthe motion has no turning points
Figure gives the x-t plot of a particle is one dimensional motion. Give the signs of position, velocity and acceleration of the particle at t = 0.3s

View SolutionWhich of the following graphs cannot represent one dimensional motion of a particle?
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in the figure. Which of the following formulae is correct for describing the motion of the particle over the time interval t1 to t2?
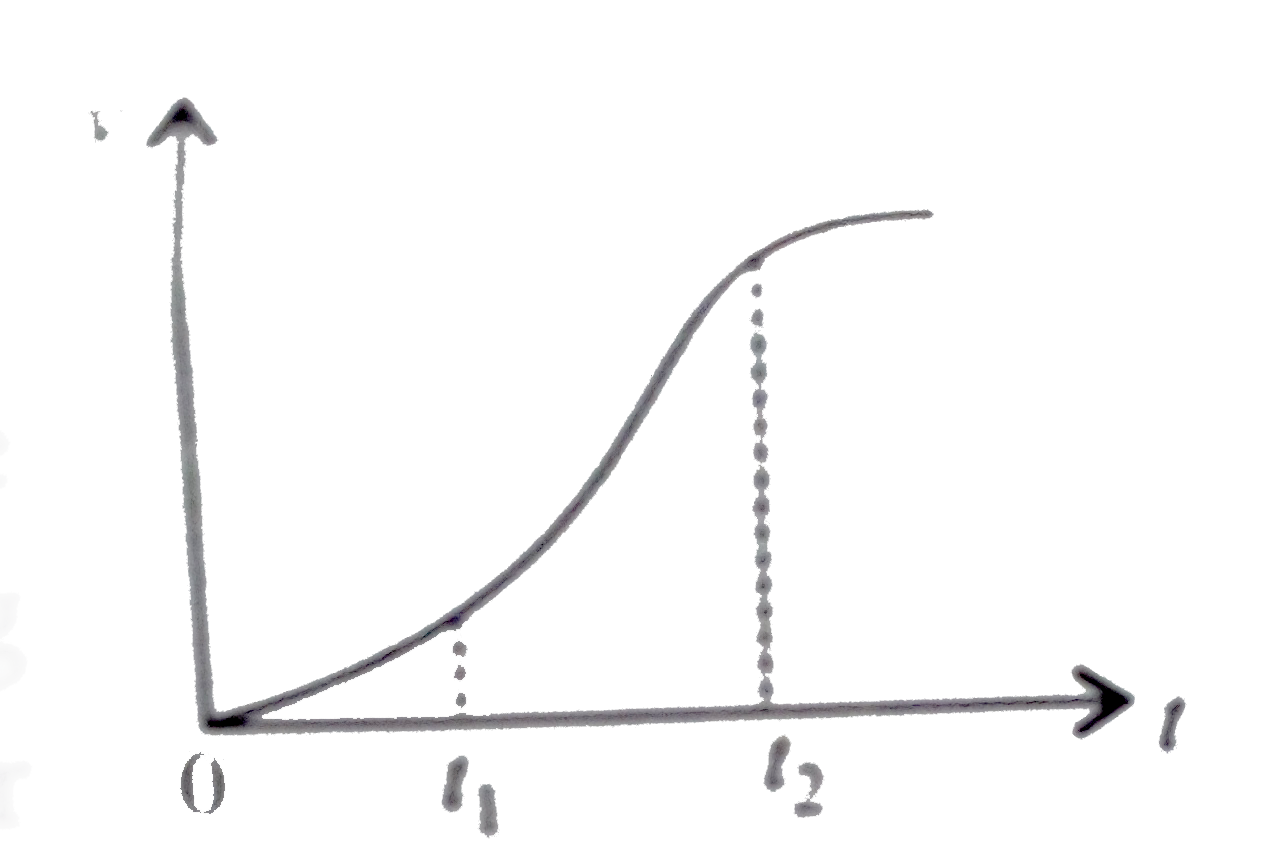
View SolutionDuring one dimensional motion on x-axis Velocity time graph for particle is given.
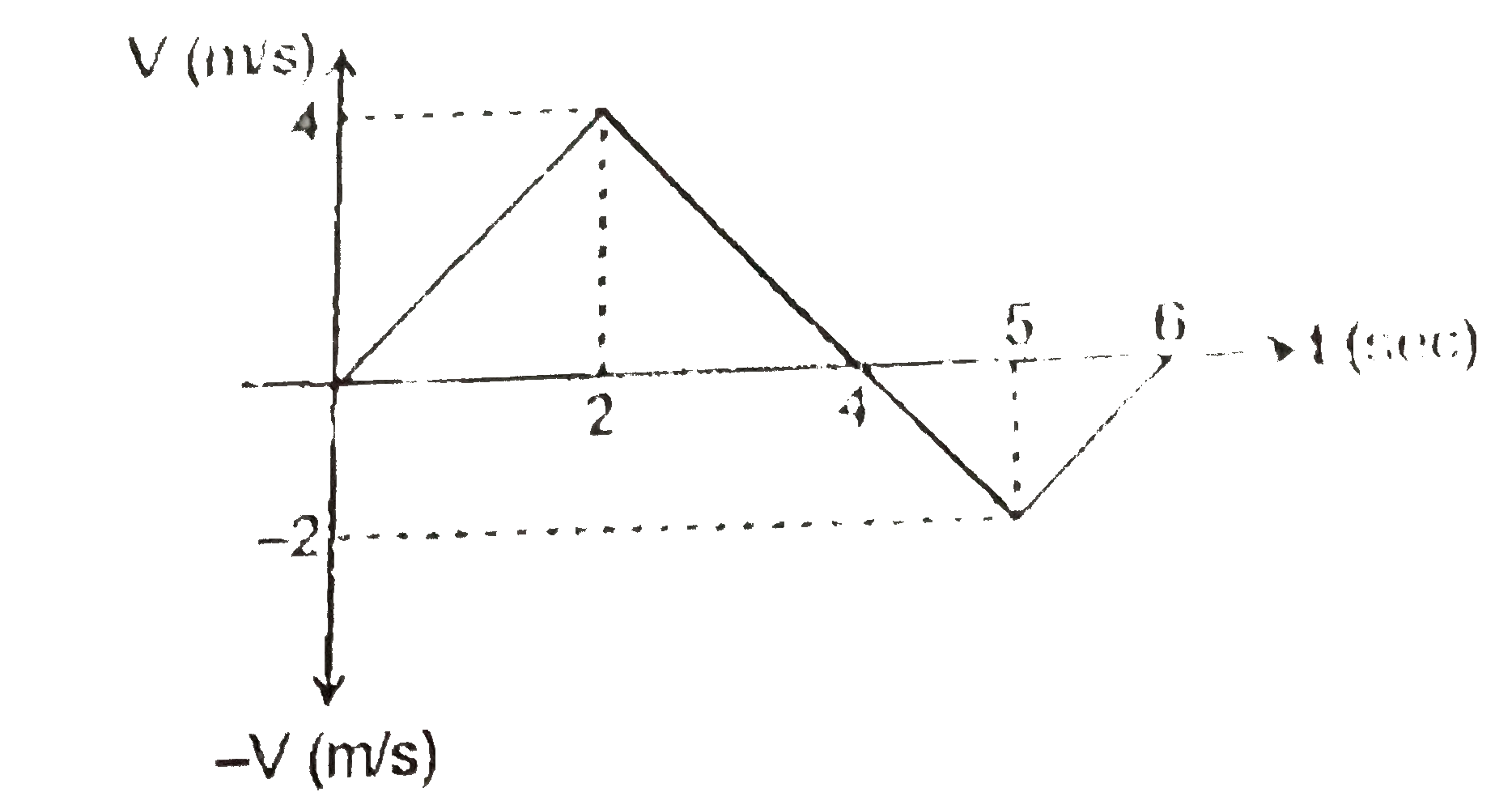
Average acceleration between (t = 0 sec) to (t = 6 sec)
View SolutionA body is initially at rest. It undergoes one dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
View Solution
