Four charges of 6μC,2μC,−12μCand4μC are placed at the corners of a square of side 1m. The square is in x-y plane and its centre is at origin. Electric potential due to these charges is zero everywhere or the line
x=y,z=0
z=0=z
x=0=y
x=z,y=0
The correct Answer is:C
To determine the line along which the electric potential due to the given charges is zero, we can follow these steps:
Step 1: Understand the Configuration
We have four charges located at the corners of a square with a side length of 1 meter. The charges are:
- Q1=6μC at (0.5, 0.5)
- Q2=2μC at (0.5, -0.5)
- Q3=−12μC at (-0.5, -0.5)
- Q4=4μC at (-0.5, 0.5)
The center of the square is at the origin (0, 0).
Step 2: Calculate the Total Charge
The total charge Qtotal is calculated as follows:
Qtotal=Q1+Q2+Q3+Q4=6μC+2μC−12μC+4μC=0μC
Since the total charge is zero, it indicates that there is a balance of positive and negative charges.
Step 3: Electric Potential Formula
The electric potential V at a point due to a point charge is given by:
V=k⋅Qr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
Step 4: Determine the Potential at a Point
To find the potential at a point P located at distance D from the center of the square (along the z-axis), we can express the potential due to each charge:
VP=k(Q1D1+Q2D2+Q3D3+Q4D4)
where D1,D2,D3,D4 are the distances from the point P to each of the charges.
Step 5: Symmetry Consideration
Due to the symmetry of the square and the arrangement of charges, the distances from the point along the z-axis to each charge will be equal. Thus, we can denote the distance from the center to any corner of the square as D:
D1=D2=D3=D4=D
Step 6: Setting Up the Equation
Substituting the charges and their distances into the potential equation, we get:
VP=k(6μCD+2μCD+4μCD−12μCD)
This simplifies to:
VP=k⋅(6+2+4−12)μCD=k⋅0D=0
Step 7: Conclusion
The electric potential is zero at any point along the z-axis (where x=0 and y=0), confirming that the electric potential due to these charges is zero everywhere along the line that is perpendicular to the square and passes through the origin.
Final Answer
The electric potential due to these charges is zero everywhere along the z-axis.
---
We have four charges located at the corners of a square with a side length of 1 meter. The charges are:
- Q1=6μC at (0.5, 0.5)
- Q2=2μC at (0.5, -0.5)
- Q3=−12μC at (-0.5, -0.5)
- Q4=4μC at (-0.5, 0.5)
The total charge Qtotal is calculated as follows:
Qtotal=Q1+Q2+Q3+Q4=6μC+2μC−12μC+4μC=0μC
Since the total charge is zero, it indicates that there is a balance of positive and negative charges.
The electric potential V at a point due to a point charge is given by:
V=k⋅Qr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
To find the potential at a point P located at distance D from the center of the square (along the z-axis), we can express the potential due to each charge:
VP=k(Q1D1+Q2D2+Q3D3+Q4D4)
where D1,D2,D3,D4 are the distances from the point P to each of the charges.
Due to the symmetry of the square and the arrangement of charges, the distances from the point along the z-axis to each charge will be equal. Thus, we can denote the distance from the center to any corner of the square as D:
D1=D2=D3=D4=D
Substituting the charges and their distances into the potential equation, we get:
VP=k(6μCD+2μCD+4μCD−12μCD)
This simplifies to:
VP=k⋅(6+2+4−12)μCD=k⋅0D=0
The electric potential is zero at any point along the z-axis (where x=0 and y=0), confirming that the electric potential due to these charges is zero everywhere along the line that is perpendicular to the square and passes through the origin.
The electric potential due to these charges is zero everywhere along the z-axis.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced44videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension36videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery21videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
Similar Questions
Electric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
View SolutionCharges 5μC,−2μC,3μCand−9μC are placed at the corners A,B,C and D of a square ABCD of side 1m. The net electric potential at the centre of th square is
View Solution
Knowledge Check
- Question 1 - Select One
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0a
Four point charges 1μC,3μC,−2μCand−2μC are arranged on the four vertices of a square of side 1 cm. The dipole moment of this charge assembly is
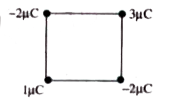 View Solution
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.
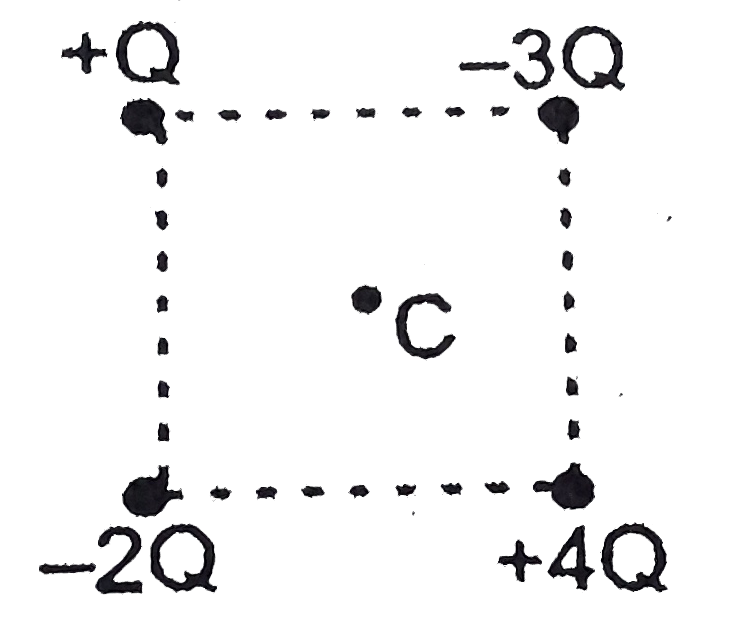 View Solution
View SolutionFour charges q1=1μC,q2=2μC,q3=−3μCandq4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
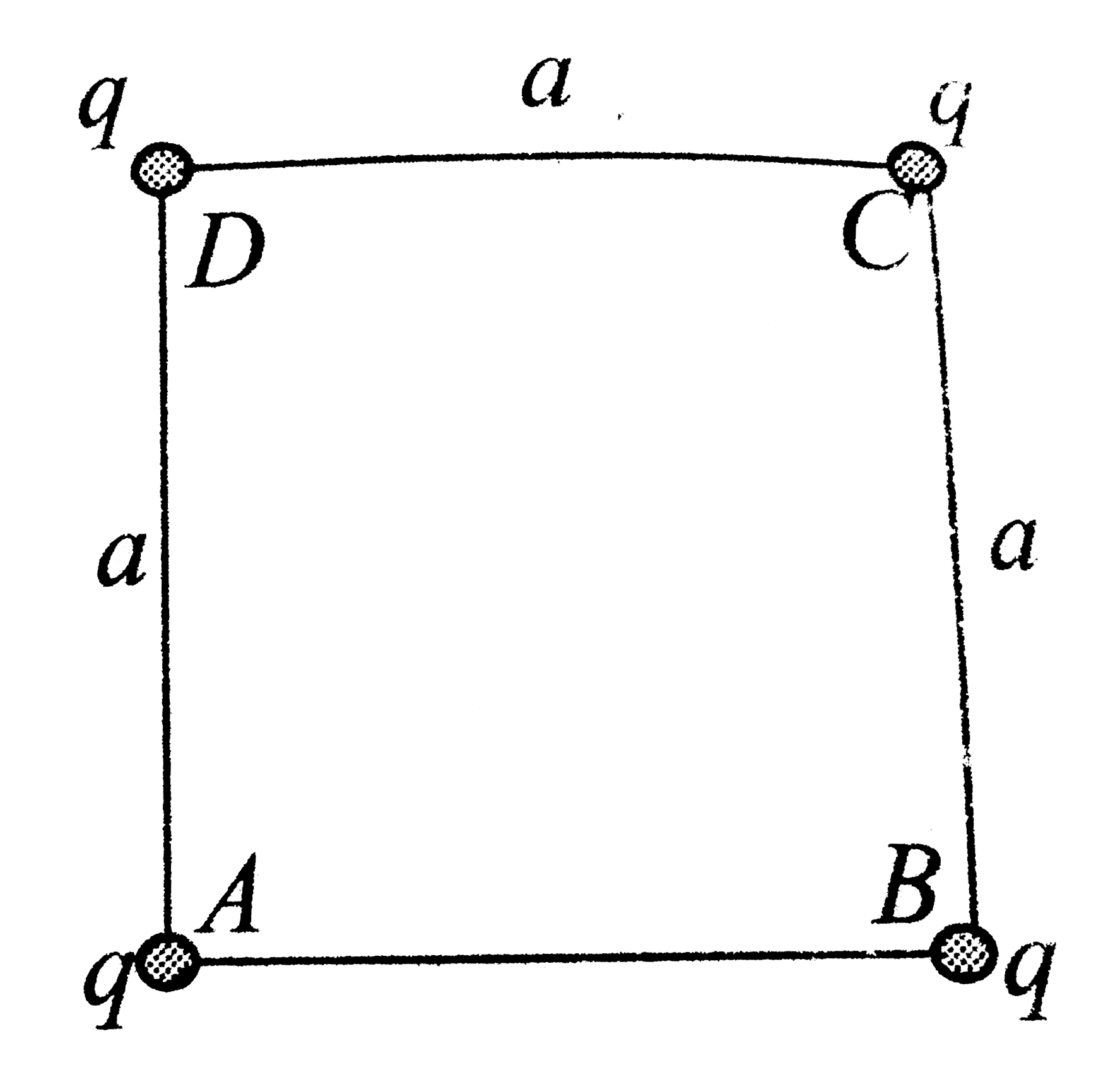 .View Solution
.View SolutionFor charges q1=1μC,q2=2μC,q3=−3μC and q4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
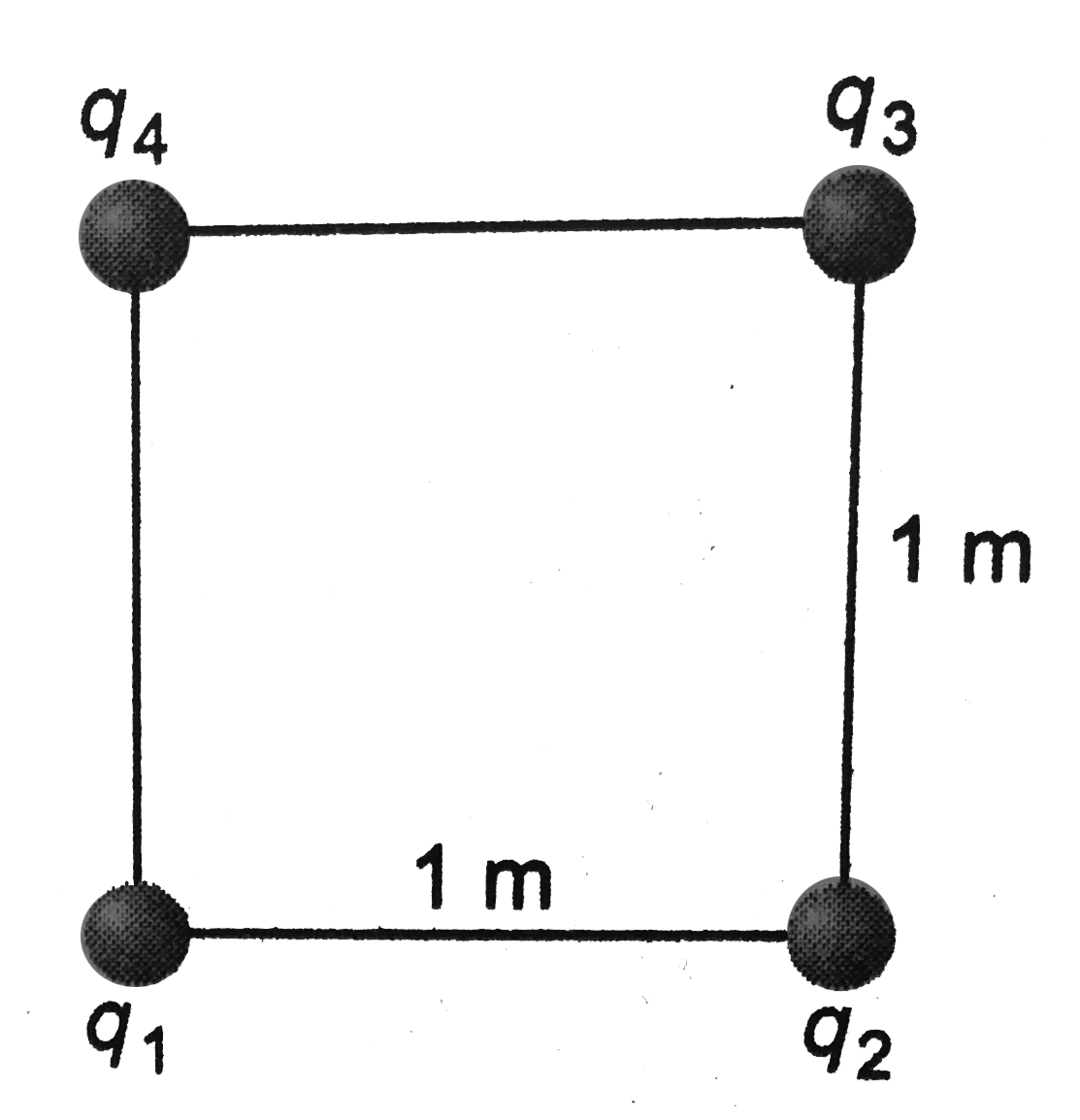 View Solution
View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is
 View Solution
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
View Solution

