
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The moment of inertia of system about the axis of ring will be-
20kgm2
40kgm2
10kgm2
60kgm2
The correct Answer is:A
I=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩M(R√2)212+M(R√2)2⎫⎪
⎪
⎪⎬⎪
⎪
⎪⎭4+mR2
=83MR2+mR2=20kgm2
(4M+m)gsinθ−f−(4M+m)a
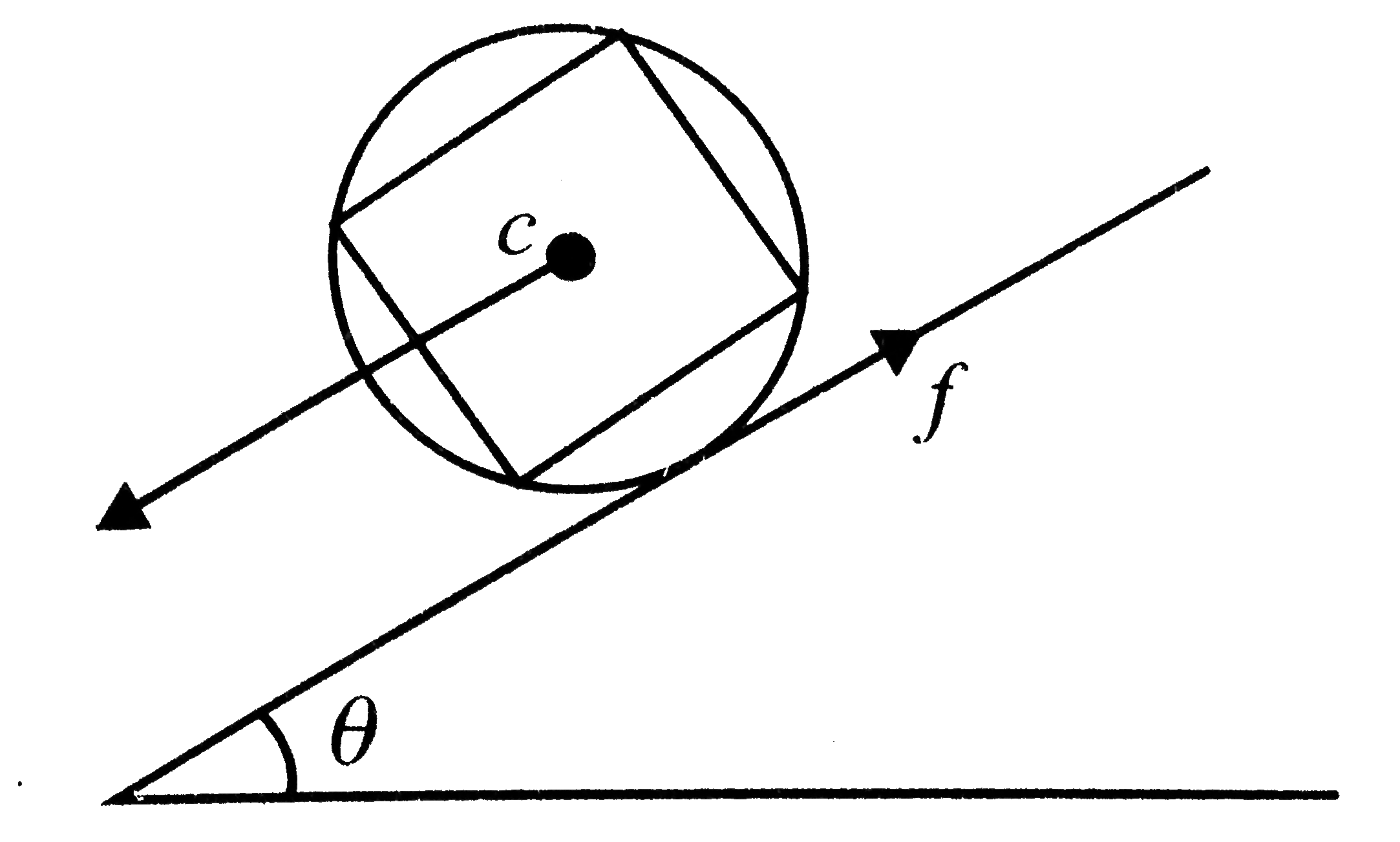
fR=IaR
Solving eqn i and ii
a=7g24
f=20a=μ×28gcos30∘
μ=512√3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Knowledge Check
- Question 1 - Select One
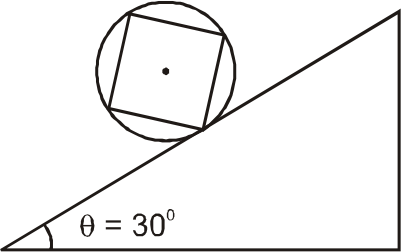
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The acceleration of centre of mass of system isAg2Bg4C7g24Dg8 - Question 2 - Select One
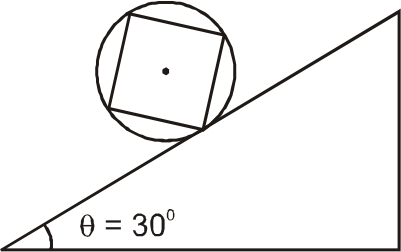
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The minimum value of coefficient of friction to prevent slipping is-A57B512√3C5√37D75√3 - Question 3 - Select One
Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
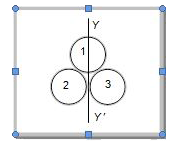 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2
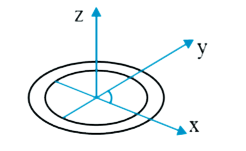
Find the moment of inertia, about a diameter, of a uniform ring of mass M = 8kg and radius a = 1m?
 View Solution
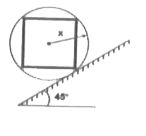
View SolutionFor identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k10 . Find the value of k.
 View Solution
View SolutionFour rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be
 View Solution
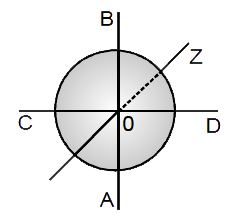
View SolutionFind the moment of inertia of uniform ring of mass M and radius R about a diameter.
 View Solution
View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be
 View Solution
View Solution



