From a uniform disc of radius R, a small disc of radius R2 is cut and removed as shown in the diagram. Find the center of mass of the remaining portion of the disc.Solution in Tamil
Let us consider the mass of the uncut full disc be M. Its center of mass would be at the geometric center of the disc on which the origin coincides. Let the mass of the small disc cut and removed be mn and its center of mass is at a position R2 to the right of the origin as shown in the figurr.

Hence, the remaining portion of the disc should have its center of mass to the left of the origin, say, at a distance x. We can write from the principle of moments,
(M−m)x=R2
x=(mM−m)R2
If σ is the surface mass density (i.e., mass per unit surface area). σMπR2 of small disc is,surface mass density surface area
m= surface mass density × surface area
m=σ×π(R2)2
m=(MπR2)π(R2)2=MπR2πR24=M4
substituting m in the expression for x x=M4(M−M4)×R2=M4(3M4)×R2
x=R6
he center of mass of the remaining portion is at a distance R6 to the left from the center of the disc.
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESBOOK - FULL MARKSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESEXERCISE - TEXTUAL QUESTIONS SOLVED ( MULTIPLE CHOICE QUESTIONS:)
15 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESBOOK - FULL MARKSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIESEXERCISE - TEXTUAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIOS)
17 Videos
- LAW OF MOTION BOOK - FULL MARKSCHAPTER - LAW OF MOTION EXERCISE - ADDITIONAL QUESTIONS SOLVED (SHORT ANSWER QUESTIONS (3 MARKS & NUMERICALS))
16 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENT BOOK - FULL MARKSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENT EXERCISE - ADDITIONAL QUESTIONS SOLVED ( SHORT ANSWER QUESTIONS (2 MARK))
20 Videos
Similar Questions
The centre of mass of a system of particles does not depend upon
View SolutionDefine the center of mass of a body.
View SolutionA block of mass 500 g is at rest on a horizontal table. What steady force is required to give the block a velocity of 200cms−1 in 4 s?
View SolutionThe vernier scale of a travelling microscope has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm. Calculate the minimum inaccuracy in the measurement of distance.
View SolutionGiven a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2 R such that the circumferences of the discs coincide. The center of mass of new disc is alpha R from the center of the bigger disc. The value of alpha is
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius a2 is cut from disc of radius a.
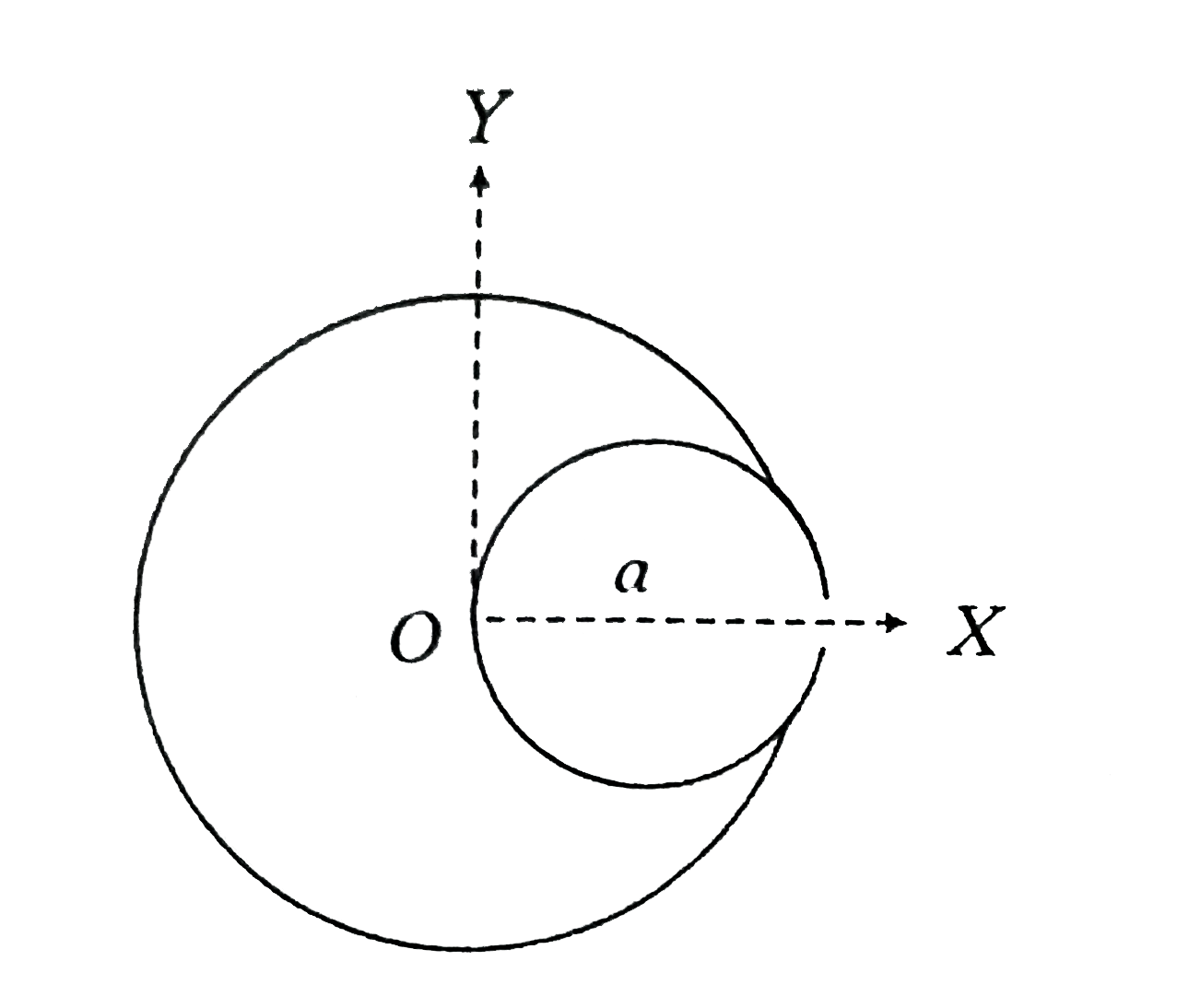
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA circular disc of radius (R)/(4) is cut from a uniform circular disc of radius R. The centre of cut portion is at a distance of (R)/(2) from the centre of the disc from which it is removed. Calculate the centre of mass of remaining portion of the disc.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA disc of radius R is cut from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the remaining portion is at
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View Solution
