From the ceiling of a train, a pendulum of length 'l' is suspended. The train is moving with an acceleration a0 on horizontal surface. What must be the period of oscillation of pendulum?
T=2π√lg
T=2π√lg+a
T=2π√l(g2+a2)1/2
T=2π√l(g2−a2)1/2
The correct Answer is:C
As g and a are perpendicular to each other
∴ Net acceleration =√g2+a2
∴T=2π
⎷l(√(g2+a2)1/2)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-1
1 Videos
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-2
1 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MARVEL PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - TEST YOUR GRASP
30 Videos
- COMMUNICATION SYSTEMS BOOK - MARVEL PUBLICATIONCHAPTER - COMMUNICATION SYSTEMS EXERCISE - TEST YOUR GRASP -20
10 Videos
Similar Questions
A simple pendulum whose length is 20 cm is suspended from the ceiling of a lift which is rising up with an acceleration of 3.0ms−2. Calculate the time-period of the pendulum.
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
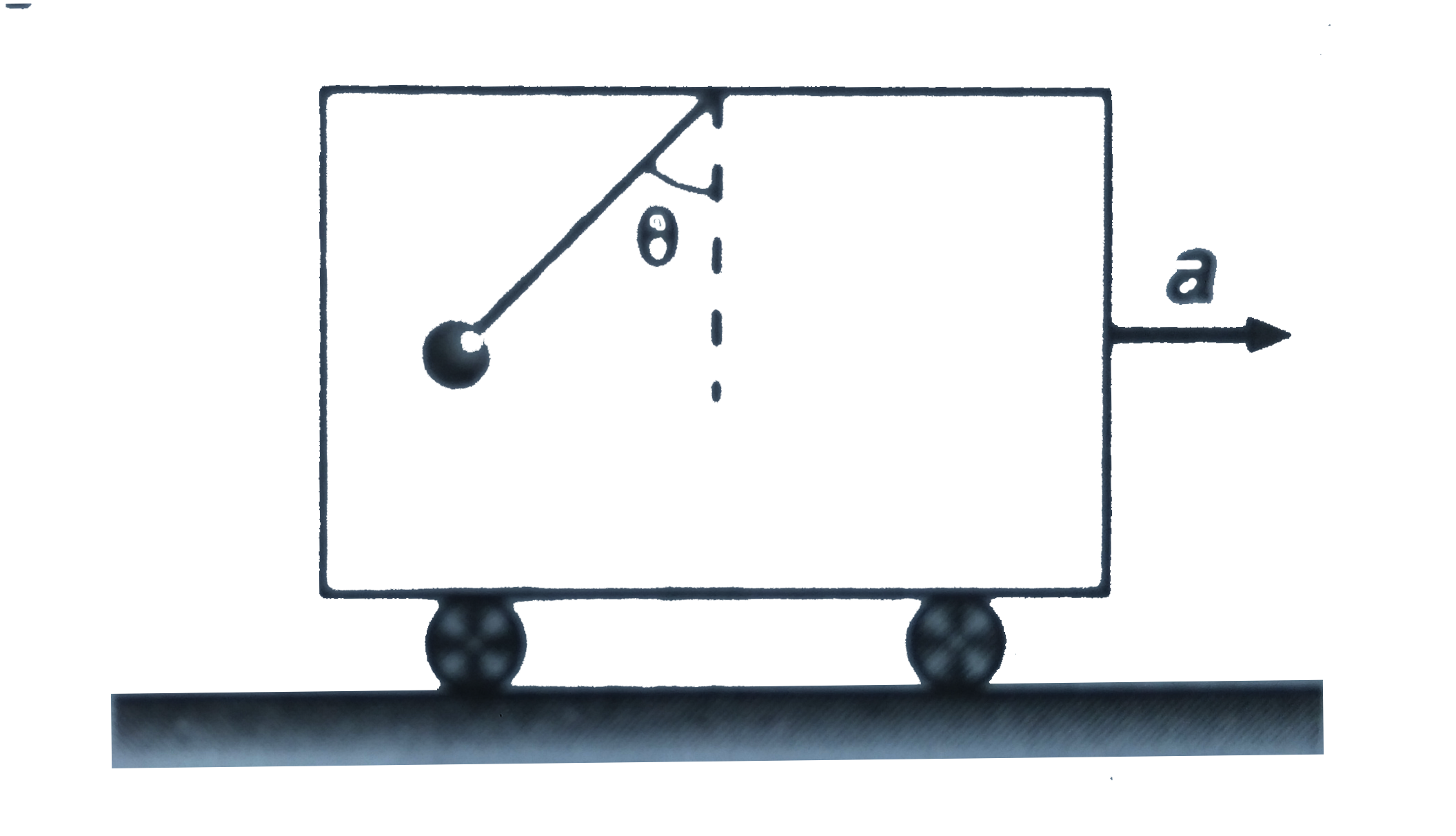
View Solution
Knowledge Check
The pendulum suspended from the ceiling of a train has a period T when the train is at rest. When the train is accelrating with a uniform acceleration, the period of oscillation will
AincreaseBdecreaseCremain unaffectedDbecome infiniteA simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
AT=2π√lgBT=2π√lg+aCT=2π√l(g2+a2)DT=2π√lg−aA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
A1.90sB1.70sC2.30sD1.40s
A pendulum is suspended in a lit and its period of oscillation is T0 when the lift is stationary.
(i) What will be the period T of oscillation of pendulum, if the lift begins to accelerates downwards with an acceleration equal to 3g4 ?
(ii) What must be the accleration of the lift for the period of oscillation of the pendulum to be T02 ?
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA plumb line is suspended from a ceiling of a car moving with horizontal acceleration of a . What will be the angle of inclination with vertical
View SolutionA pendulum suspended from the ceiling of a train has time period T when the train is at rest .When the train is accelerating with a uniform acceleration ,the time period will
View SolutionAa simple pendulum is suspended from the ceiling of a vehicle which moves down an inclined plane o inclination Θ. The period of oscilation of the pendulum is
View Solution
