From the top of a tower, two particles are dropped at an interval of 2 s . Find the relative velocity and relative acceleration of the particles during the fall . Acceleration due to gravity =g . Solution in Bengali
The correct Answer is:2g ,0
Step by step video, text & image solution for From the top of a tower, two particles are dropped at an interval of 2 s . Find the relative velocity and relative acceleration of the particles during the fall . Acceleration due to gravity =g cm*s^(-2). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTORBOOK - CHHAYA PUBLICATIONCHAPTER - VECTOREXERCISE - PROBLEM SET-II
34 Videos
- VECTORBOOK - CHHAYA PUBLICATIONCHAPTER - VECTOREXERCISE - PROBLEM SET-II (Hot Numerical Problems)
24 Videos
- VECTORBOOK - CHHAYA PUBLICATIONCHAPTER - VECTOREXERCISE - EXERCISE (Short Answer Type Questions-II)
2 Videos
- THERMOMETRYBOOK - CHHAYA PUBLICATIONCHAPTER - THERMOMETRYEXERCISE - EXAMINATION ARCHIEVE - WBJEE
1 Videos
- VISCOSITY AND SURFACE TENSIONBOOK - CHHAYA PUBLICATIONCHAPTER - VISCOSITY AND SURFACE TENSIONEXERCISE - EXERCISE (CBSE SCANNER)
9 Videos
Similar Questions
Resultant of two forces P and Q is √3Q. The resultant is inclined at 30∘ with P . Show that, either P =Q or P=2Q.
View SolutionOne motor launch A is exactly 1 km north of another launch B. Both launches start from rest , at the same time, with an acceleration of 10cm⋅s−2. The launch A proceeds towards east and B towards north. Find the distance of closest approach between them and the time taken to reach that distance.
View SolutionAngle between the vectors →Aand→B is θ. By resolving them into mutually perpendicular components show that the magnitude of the resultant vector is (A2+B2+2ABcosθ)1/2.
View SolutionA scientist proposes a new temperature scale in which the ice point is 25X (X is the new unit of temperature) and the steam point is 305X. The specific heat capacity of water in this new scale is (in J⋅kg−1⋅X−1)
View SolutionState and prove Bernoulli's theorem.
View SolutionA particle is moving with a velocity of v=(3+ 6t +9t^2) m/s . Find out (a) the acceleration of the particle at t=3 s. (b) the displacement of the particle in the interval t=5s to t=8 s.
View SolutionThe v−s and v2−s graph are given for two particles. Find the accelerations of the particles at s=0.
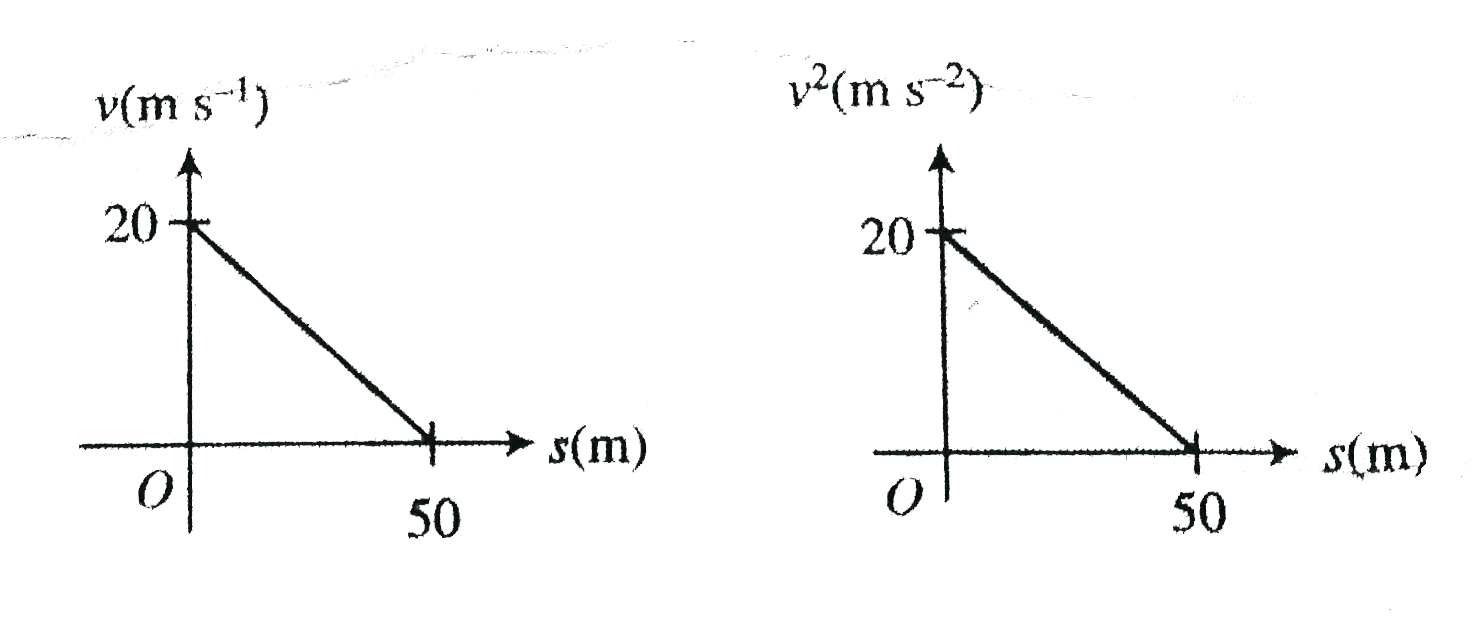 .
.
View SolutionA particle starts from rest with acceleration 2m/s2. The acceleratioin of the particle of the particle descreases down to zero uniformly during time -interval of 4s. The velocity of particle after 2s is
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionIf velocity of a particle is given by v=2t2−2 then find the acceleration of particle at t = 2 s.
View SolutionParagraph- Two particles are projected simultaneously from the top of a tower of height 80m horizontally in mutually perpendicular directions at equal speed of 40m/s. Q.The relative velocity of particles when they strike the ground is: m/s
View SolutionThe velocity of a particle is given by the equation, v=2t2+5cms−1 . Find
the average acceleration during the time interval betweent1=2sandt2=4s .
View SolutionThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as Dwhere particle finally strikes. Acceleration due to gravity g=10m/s2
Maximum height above the ground attained by particle is
View SolutionThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
Time taken by the particle to reach the ground is
View SolutionAcceleration due to gravity g=__________ m//s^2 .
View Solution
