Give the name of the points in a stationary wave at which (i) velocity is zero (ii) displacement is zero and (iii) strain is maximum.
To solve the question regarding stationary waves, we need to identify the points where the velocity, displacement, and strain are at specific values. Let's break this down step by step.
1. Understanding Stationary Waves:
- Stationary waves are formed by the interference of two waves traveling in opposite directions. They consist of nodes and antinodes.
2. Identifying Points of Zero Velocity:
- In a stationary wave, the points where the particles do not move are called nodes. At these points, the velocity of the particles is zero because they oscillate around a fixed position.
Answer: Velocity is zero at nodes.
3. Identifying Points of Zero Displacement:
- The displacement of the particles is also zero at the nodes. This means that at these points, the particles do not move away from their equilibrium position.
Answer: Displacement is zero at nodes.
4. Identifying Points of Maximum Strain:
- Strain is related to the change in displacement. In a stationary wave, strain is maximum at the nodes because this is where the pressure variation is greatest. At nodes, the particles are at their equilibrium position, leading to maximum compression or rarefaction.
Answer: Strain is maximum at nodes.
Final Answers:
- (i) Velocity is zero at nodes.
- (ii) Displacement is zero at nodes.
- (iii) Strain is maximum at nodes.
- Stationary waves are formed by the interference of two waves traveling in opposite directions. They consist of nodes and antinodes.
- In a stationary wave, the points where the particles do not move are called nodes. At these points, the velocity of the particles is zero because they oscillate around a fixed position.
- The displacement of the particles is also zero at the nodes. This means that at these points, the particles do not move away from their equilibrium position.
- Strain is related to the change in displacement. In a stationary wave, strain is maximum at the nodes because this is where the pressure variation is greatest. At nodes, the particles are at their equilibrium position, leading to maximum compression or rarefaction.
- (i) Velocity is zero at nodes.
- (ii) Displacement is zero at nodes.
- (iii) Strain is maximum at nodes.
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Doppler Effect, Musical, Sound, Noise
26 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Very Short Answer Questions
14 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Short Answer Questions.
32 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
Displacement versus time curve for a particle executing SHM is shown in figure. Identify the points marked at which
(i) velocity of the oscillator is zero,
(ii) speed of the oscillator is maximum.
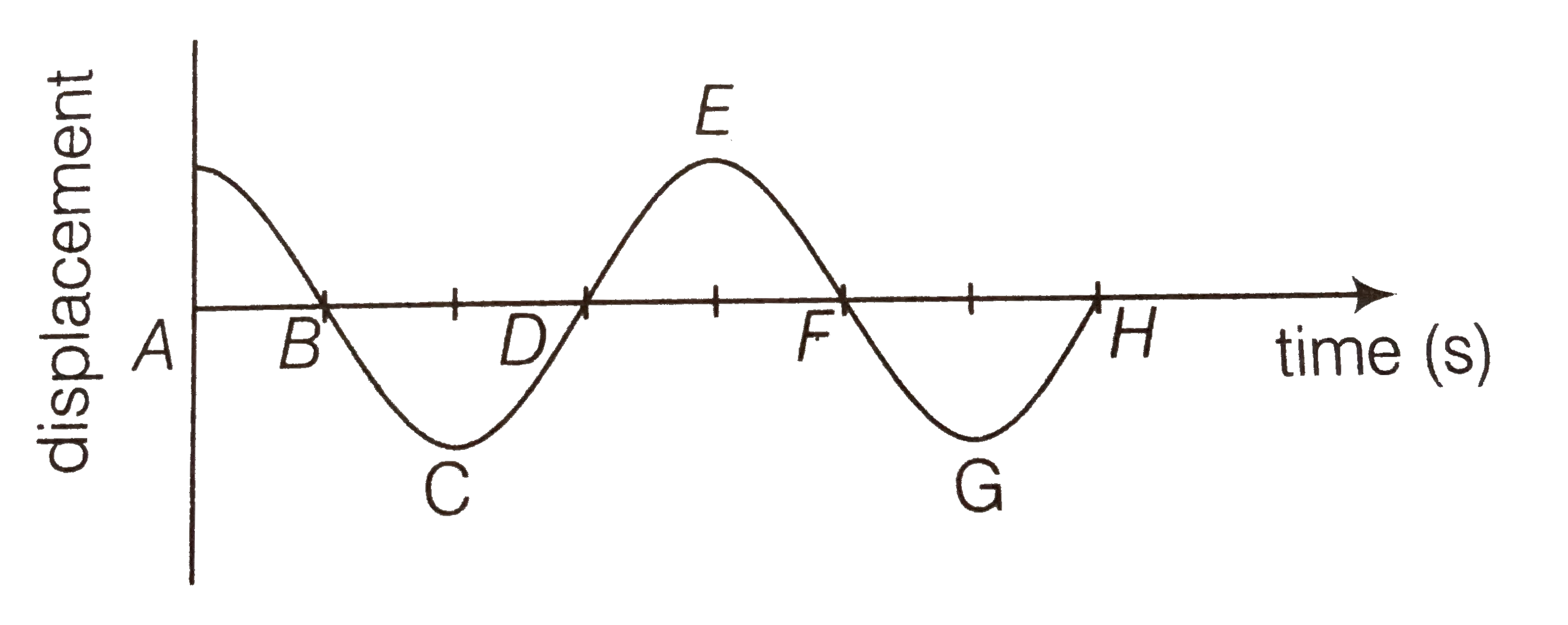
View SolutionIf the displacement is zero, velocity is ……………….....(maximum/zero).
View SolutionStatement I: The displacement of a body may be zero, though its distance can be finite.
Statement II: If the bodt moves such that finally it arrives at the initial point, then displacement is zero while distance is finite.
View SolutionAt which point of a stationary wave the sound heard is maximum, at the node or the antinode ?
View SolutionConsider the motion of the tip of the minute hand of a clock. In one hour
(a) the displacement is zero
(b) the distance covered is zero
(c) the average speed is zero
(d) the average velocity is zero
View SolutionGive an example of motion in which average speed is not zero, but average velocity is zero.
View SolutionAt what position of a body executing shm its velocity (i) maximum and (ii) zero ?
View SolutionGive an example of a case where the velocity of an object is zero but its accleration is not zero?
View SolutionGive examples for the particle where (a) the velocity is in opposite direction to the acceleration (b)the velocity of the particle is zero but is acceleration is not zero.
View SolutionConsider the motion of the tip of the minute hand of a clock.In one hour
a)The displacement is zero
b)The distance covered is zero
c)The average speed is zero
d)The average velocity is zero
View Solution
