How will you infer with the help of an experiment that the same current flows through every part of the circuit containing three resistances in series connected to a battery ?
To demonstrate that the same current flows through every part of a circuit containing three resistances in series connected to a battery, we can conduct a simple experiment. Below are the step-by-step instructions for the experiment:
1. Gather Materials:
- You will need three resistors (R1, R2, R3), a battery, an ammeter, and three voltmeters.
2. Set Up the Circuit:
- Connect the three resistors in series. This means that one end of R1 is connected to the positive terminal of the battery, the other end of R1 is connected to one end of R2, and the other end of R2 is connected to one end of R3. Finally, connect the other end of R3 back to the negative terminal of the battery.
3. Connect the Ammeter:
- Insert the ammeter in series with the resistors. This means that the ammeter should be connected in such a way that all the current flowing through the circuit also flows through the ammeter.
4. Connect the Voltmeters:
- Connect one voltmeter across each resistor. This means:
- Connect the first voltmeter (V1) across R1,
- Connect the second voltmeter (V2) across R2,
- Connect the third voltmeter (V3) across R3.
5. Take Readings:
- Turn on the battery and note the reading on the ammeter (let’s call this I). This reading represents the total current flowing through the circuit.
- Record the voltage readings from each voltmeter (V1, V2, and V3).
6. Calculate Current Through Each Resistor:
- Using Ohm's Law (I = V/R), calculate the current through each resistor:
- For R1: I1=V1R1
- For R2: I2=V2R2
- For R3: I3=V3R3
7. Compare the Currents:
- Compare the calculated currents I1,I2, and I3 with the reading from the ammeter (I). Since the resistors are in series, the current through each resistor should be the same, i.e., I1=I2=I3=I.
8. Conclusion:
- If the calculated currents through each resistor are equal to the current measured by the ammeter, you can conclude that the same current flows through every part of the circuit.
- You will need three resistors (R1, R2, R3), a battery, an ammeter, and three voltmeters.
- Connect the three resistors in series. This means that one end of R1 is connected to the positive terminal of the battery, the other end of R1 is connected to one end of R2, and the other end of R2 is connected to one end of R3. Finally, connect the other end of R3 back to the negative terminal of the battery.
- Insert the ammeter in series with the resistors. This means that the ammeter should be connected in such a way that all the current flowing through the circuit also flows through the ammeter.
- Connect one voltmeter across each resistor. This means:
- Connect the first voltmeter (V1) across R1,
- Connect the second voltmeter (V2) across R2,
- Connect the third voltmeter (V3) across R3.
- Turn on the battery and note the reading on the ammeter (let’s call this I). This reading represents the total current flowing through the circuit.
- Record the voltage readings from each voltmeter (V1, V2, and V3).
- Using Ohm's Law (I = V/R), calculate the current through each resistor:
- For R1: I1=V1R1
- For R2: I2=V2R2
- For R3: I3=V3R3
- Compare the calculated currents I1,I2, and I3 with the reading from the ammeter (I). Since the resistors are in series, the current through each resistor should be the same, i.e., I1=I2=I3=I.
- If the calculated currents through each resistor are equal to the current measured by the ammeter, you can conclude that the same current flows through every part of the circuit.
Topper's Solved these Questions
Similar Questions
Calculate the current flowing through a wire of resistance 7.5 Ω connected to a battery of potential difference 1.5. V.
View SolutionIn the given circuit current flowing through 2 Omega resistance is
View SolutionIn the circuit, the current flowing through 10Ω resistance is
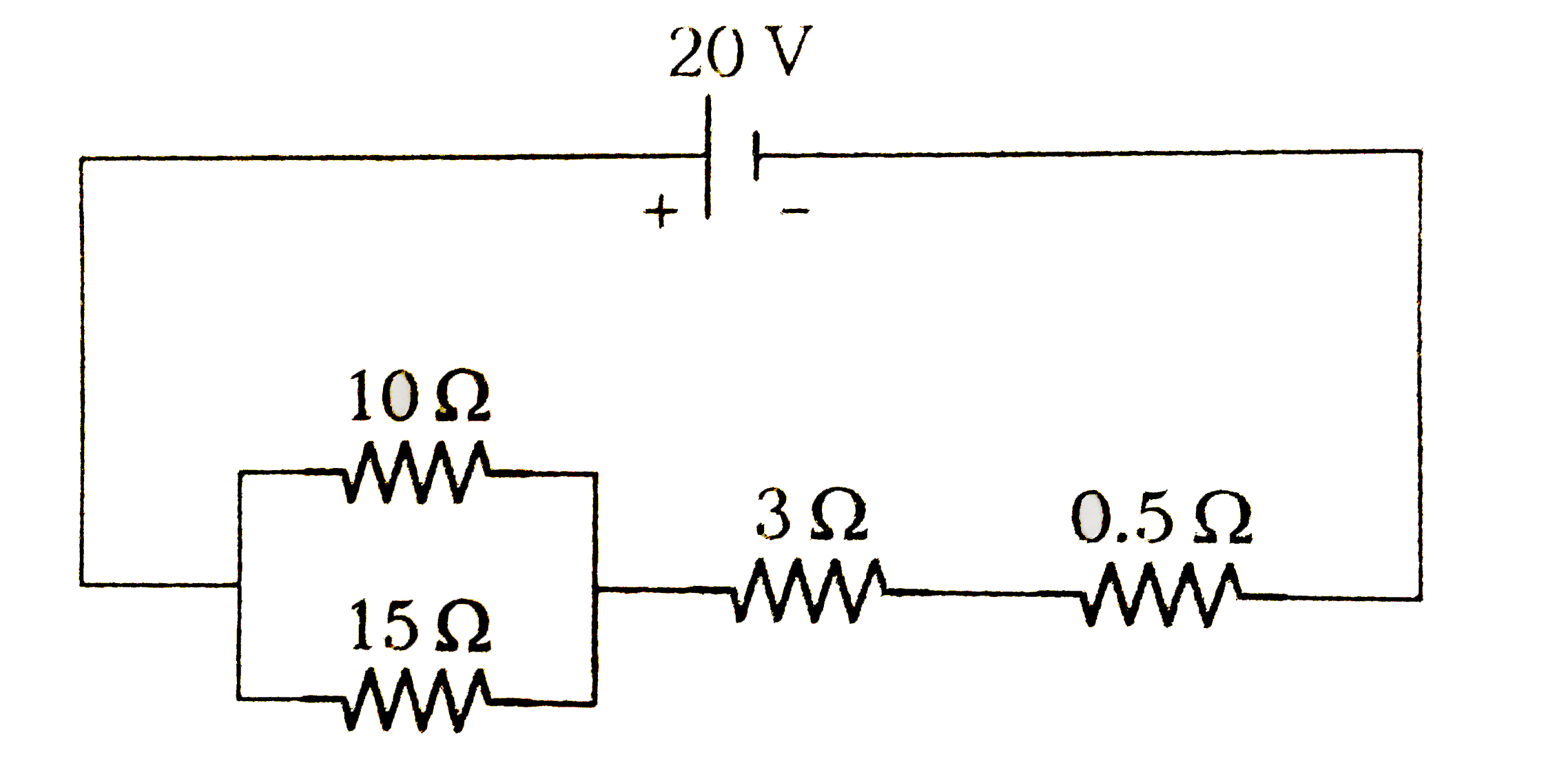 View Solution
View SolutionCalculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
View SolutionIf internal resistance of cell is negligible, then current flowing through the circuit is
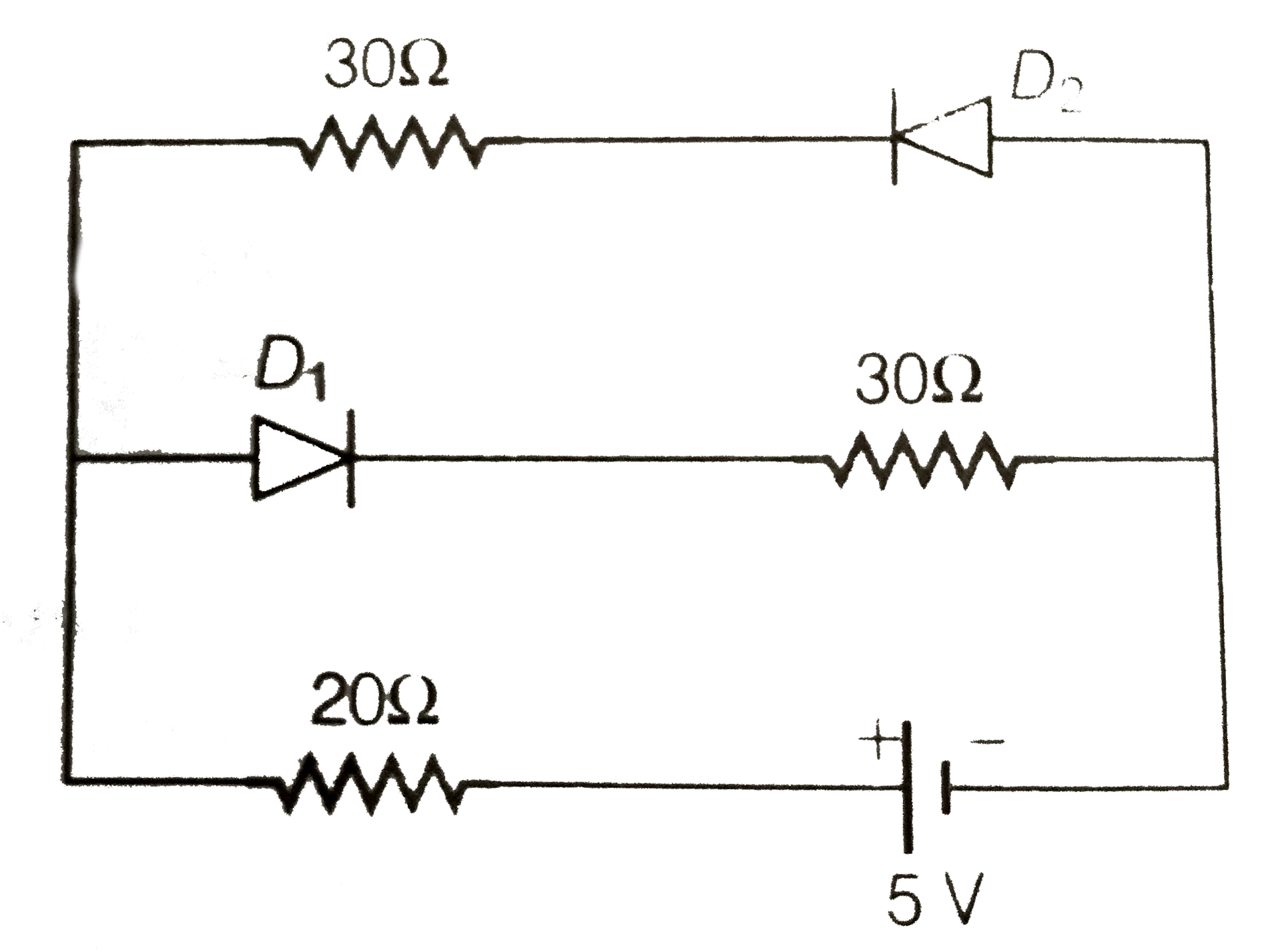 View Solution
View SolutionHow will you conclude that the same potential difference (voltage) exists across three resistors connected in a parallel arrangement to a battery ?
View SolutionFind out the magnitude of resistance X in the circuit shown in figure, When no current flows through the 5Ω resistance
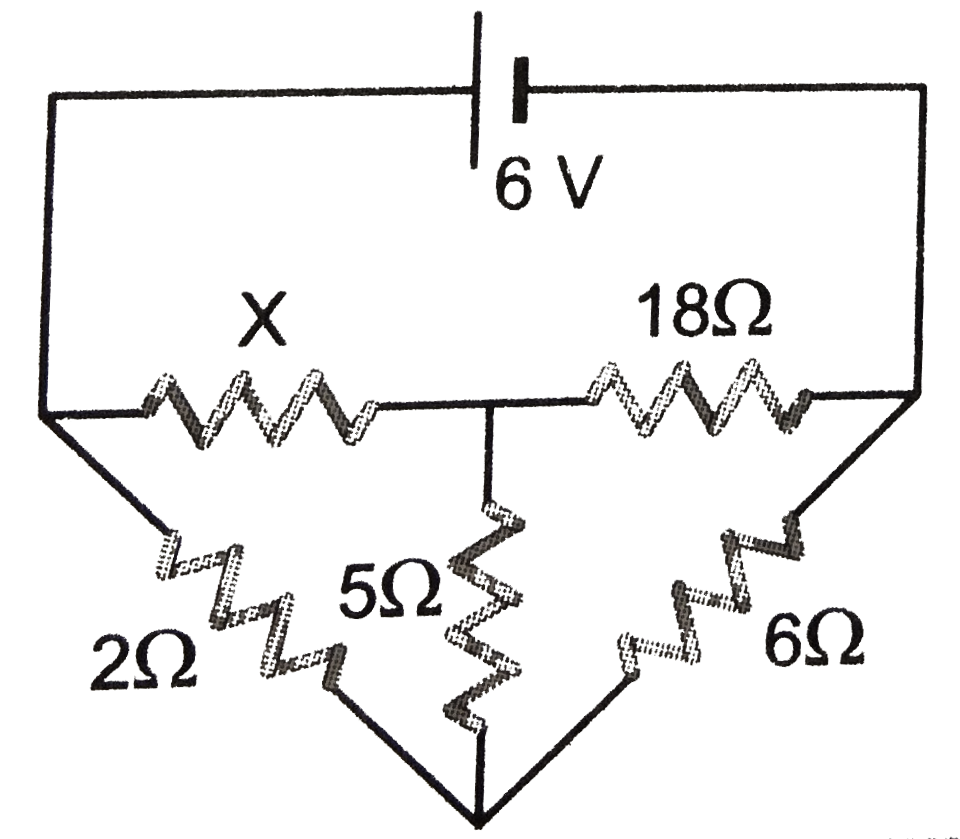 View Solution
View SolutionThree capacitors each having capacitance C=2μF are connected with a battery of emf30V as shown in. when the switch S is closed, find
a. the amount of charge flowing through the battery ,
b. the heat generated in the circuit,
c. the energy supplied by the battery,
d. the amount of charge flowing through the switch S.
 .View Solution
.View SolutionIn the circuit shown in figure points a, b and c are maintained at constant (but may be different) potentials. When a resistance is connected between a and b no current flows through it, when the same resistance is connected between b and c current flows from c to b.
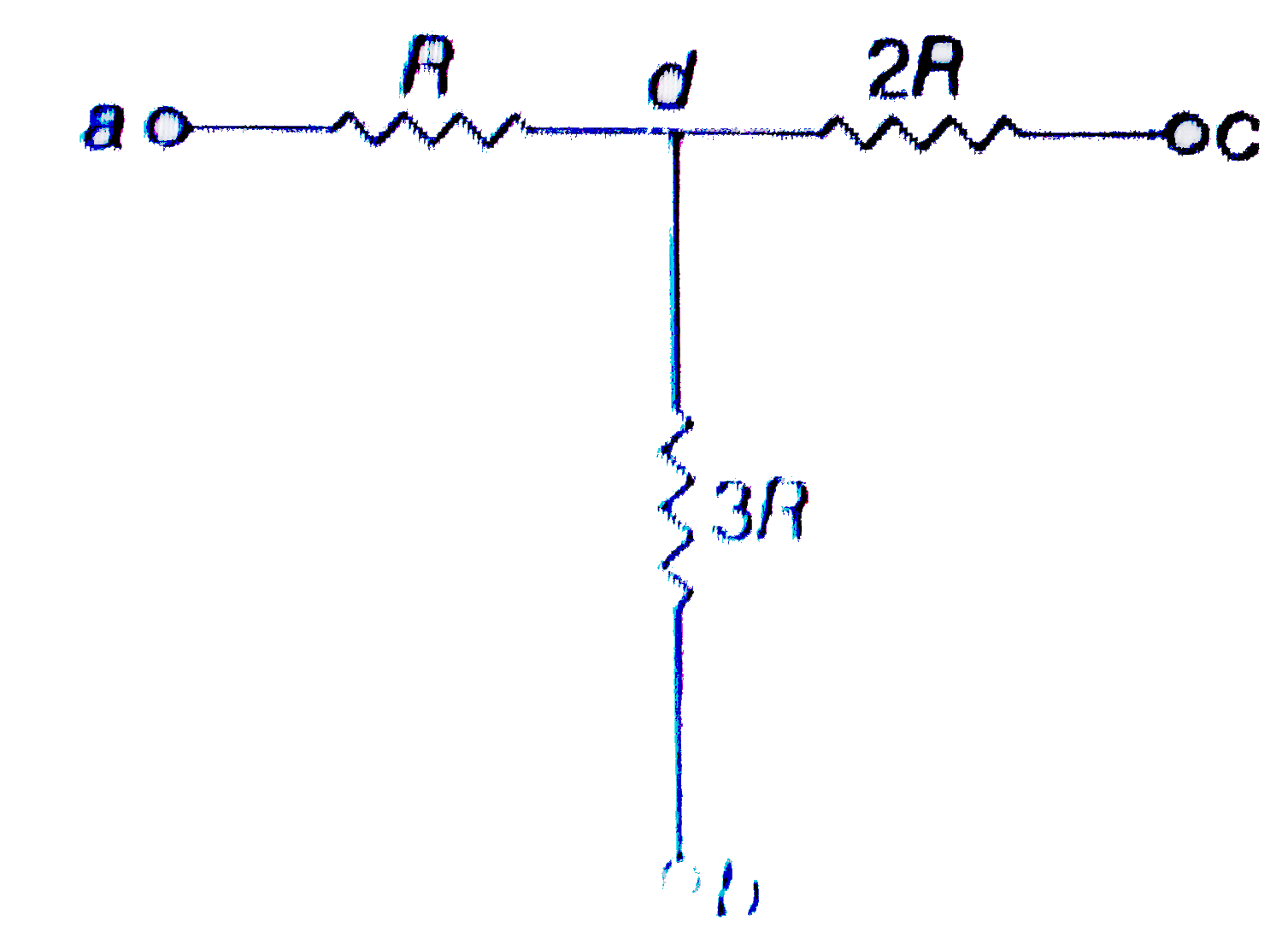
When only three resistance shown in figure are in the circuitView SolutionA constant current exists in an inductor coil connected to a battery. The coil is short circuited and the battery is removed. Show that the charge flown through the coil after the short circuiting is the same as that which flows in one time constant before the short circuiting.
View Solution

