If look inside a real piano , you'll see that the assumption made in part (b) of Illustration 7.31 is only partially true . The strings are not likely to have the length of the A string is only 64% of the length of the C string . What is the ratio of their tensions ?
The ratio of frequencies :
f1Af1C=LCLA√TATC
TATC=(LALC)2(f1Af1C)2
TATC=(0.64)2(440262)2=1.16
Notice that this result represents only a 16% increase in tension , compares with the 18.2% increase in part (b) of Illustration 7.31.
Similar Questions
The vibrational frequency of a string is 300 Hz. The tension in the string is made twice and the length of the string is changed in such a way that it vibrates with a frequency of 600 Hz. What will be the ratio of new length to original length ?
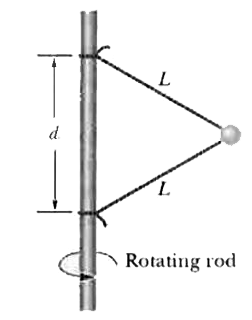
View SolutionIn fig 1.34 kg ball is connected by means of two mass less strings, each of length L=1.70m, to a vertical, rotating rod. The strings are tied to the rod with separation d=1.70 m and are taut. The tenion in the upper string is 35N. What are the (a) tension in the lower string, (b) magnitude of the net (b) magnitude of the net force →Fnet on the all, and (c) speed of the ball? (d) What is the direction of →Fnet?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two stretched strings have lengths 1 and 21 while tensions are T and 4 T respectively. If they are made of same material the ratio of their frequency is
A2:1B1:2C1:1D1:4 - Question 2 - Select One
Two uniform strings A and B made of steel are made to vibrate under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is :-
A1 : 2B1 : 3C1 : 4D1 : 6 - Question 3 - Select One
Two uniform strings AandB made of steel are made to vibrate under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is
A2:1B3:2C3:4D1:3
A string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?
 View Solution
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?
 View Solution
View SolutionTwo uniform strings AandB made of steel are made to vibrate under the same tension. If the first overtone of A is equal to the second overtone of B and if the radius of A is twice that of B, the ratio of the lengths of the strings is
View SolutionA standing wave is set up in a string of a variable length and tension by a vibrator of variable frequency . Both ends of the string are fixed . When the vibrator has a frequency f , in a string of length L and under tension T,n antinodes are set up in the string is doubled , by what factor should the frequency be changed so that the same number of antinodes is produced? (b) If the frequency and lenght are held constant , what tension will produce n+1 antinodes ? ( c) If the frequency is tripled and the length of the string is halved , by what factor should the tension be changed so that twice as many antinodes are produced ?
View SolutionA sinusoidal transverse wave travel on a string. The string has length 8.00m and mass 6.00g. The wave speed is 30.0m/s and the wavelength is 0.200m. (a) If the wave is to have an average power of 50.0W, what must be the amplitude of the wave? (b) For the same string, if the ampitude and wavelength are the same as in part (a) what is the average power for the wave if the tension is increased such that the wave speed is doubled?
View Solution

