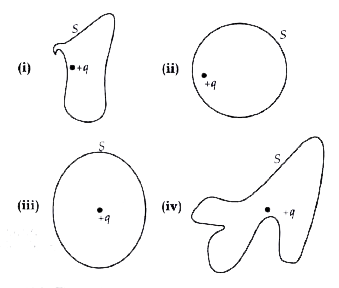If the radius of the Gaussion surface enclosing a charge q is halved, how does the electric flux through the Gaussion surface change?
To solve the problem, we will use Gauss's Law, which states that the electric flux (Φ) through a closed surface is directly proportional to the charge (q) enclosed within that surface. The mathematical expression for Gauss's Law is given by:
Φ=qϵ0
where:
- Φ is the electric flux,
- q is the charge enclosed,
- ϵ0 is the permittivity of free space.
1. Understand the Setup: We have a charge q enclosed within a Gaussian surface. The radius of this Gaussian surface is halved.
2. Apply Gauss's Law: According to Gauss's Law, the electric flux through the Gaussian surface is given by:
Φ=qϵ0
3. Consider the Effect of Changing the Radius: The problem states that the radius of the Gaussian surface is halved (from r to r2). However, Gauss's Law indicates that the electric flux depends only on the charge enclosed and not on the size or shape of the Gaussian surface.
4. Conclusion: Since the charge q enclosed by the Gaussian surface remains the same regardless of the change in radius, the electric flux through the surface also remains the same:
Φ=qϵ0
Therefore, the electric flux does not change when the radius of the Gaussian surface is halved.
Final Answer:
The electric flux through the Gaussian surface does not change when the radius is halved.
- Φ is the electric flux,
- q is the charge enclosed,
- ϵ0 is the permittivity of free space.
Φ=qϵ0
Φ=qϵ0
Therefore, the electric flux does not change when the radius of the Gaussian surface is halved.
The electric flux through the Gaussian surface does not change when the radius is halved.
Similar Questions
Knowledge Check
The electric flux through the surface
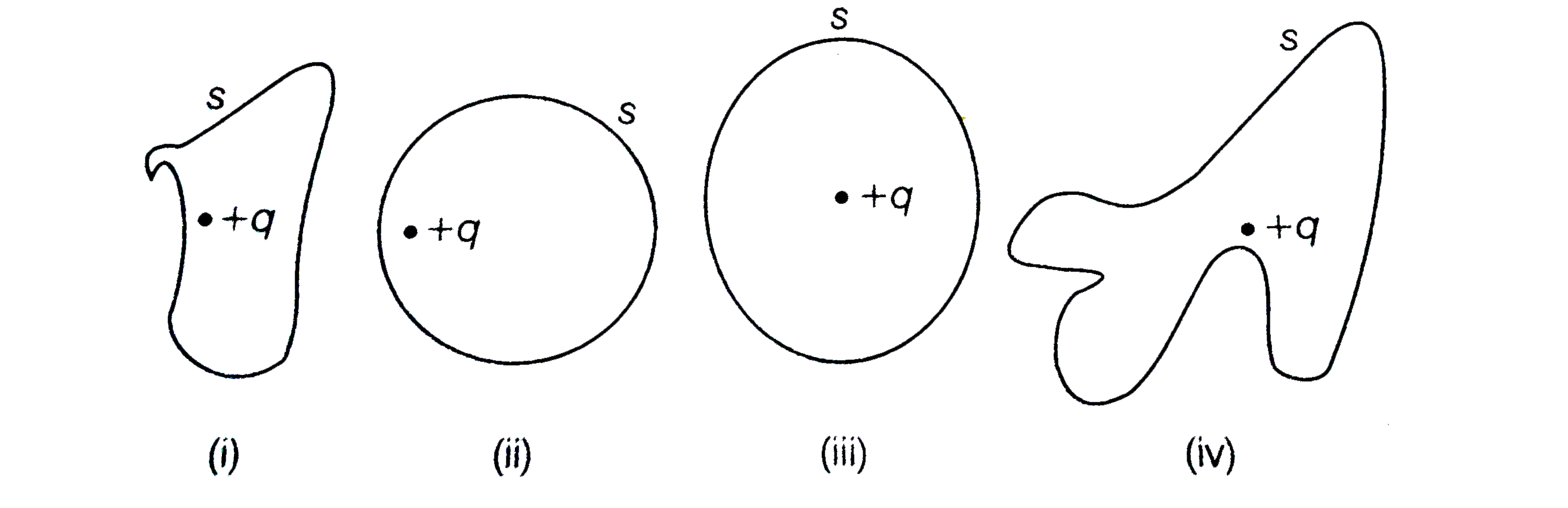 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.A charge q is enclosed as shown below the electric flux is
 Amaximum inBmaximum inCmaximum inDequal in all
Amaximum inBmaximum inCmaximum inDequal in all
An arbitrary surface encloses a dipole. What is the electric flux through this surface ?
View SolutionDefine electric flux. Write its SI unit. A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change ?
View SolutionA charge q is enclosed as shown, below the electric flux is
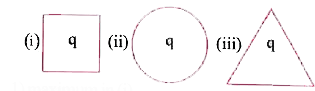
View SolutionA cube of side L encloses a charge Q at its centre , electric flux through the cube is
View SolutionA point charge causes an electric flux of −200Nm2/C to pass through spherical Guassian surface of 10 cm radius centered on the charge. If the radius of the Guassian surface is doubled, the total electric flux passing through the surface is
View Solution