If two person A and B take 2 s and 4 s, respectively to lift an object to the same height h, then the ratio of their powers is
1:2
1:1
2:1
1:3
The correct Answer is:C
To solve the problem of finding the ratio of powers of two persons A and B who lift an object to the same height in different times, we can follow these steps:
1. Understand the Concept of Power:
Power is defined as the rate at which work is done. Mathematically, it is given by:
P=Wt
where P is power, W is work done, and t is the time taken.
2. Determine the Work Done:
The work done in lifting an object to a height h against gravity is given by:
W=mgh
where m is the mass of the object, g is the acceleration due to gravity, and h is the height.
3. Calculate Power for Person A:
Person A takes 2 seconds to lift the object. Therefore, the power PA for person A can be calculated as:
PA=WtA=mgh2
4. Calculate Power for Person B:
Person B takes 4 seconds to lift the same object. Therefore, the power PB for person B can be calculated as:
PB=WtB=mgh4
5. Find the Ratio of Powers:
Now, we can find the ratio of the powers of A and B:
PAPB=mgh2mgh4
Simplifying this expression:
PAPB=mgh2×4mgh=42=2
6. Final Ratio:
Therefore, the ratio of the powers of person A to person B is:
PA:PB=2:1
Conclusion:
The ratio of the powers of persons A and B is 2:1.
Power is defined as the rate at which work is done. Mathematically, it is given by:
P=Wt
where P is power, W is work done, and t is the time taken.
The work done in lifting an object to a height h against gravity is given by:
W=mgh
where m is the mass of the object, g is the acceleration due to gravity, and h is the height.
Person A takes 2 seconds to lift the object. Therefore, the power PA for person A can be calculated as:
PA=WtA=mgh2
Person B takes 4 seconds to lift the same object. Therefore, the power PB for person B can be calculated as:
PB=WtB=mgh4
Now, we can find the ratio of the powers of A and B:
PAPB=mgh2mgh4
Simplifying this expression:
PAPB=mgh2×4mgh=42=2
Therefore, the ratio of the powers of person A to person B is:
PA:PB=2:1
The ratio of the powers of persons A and B is 2:1.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS
7 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
Knowledge Check
If two persons A and B take 2 seconds and 4 seconds respectively to lift an object to the same height h, then the ratio of their potential energies at highest point is
A1:2B1:1C2:1D1:3The area of two holes A and B are 2a and a, respectively, The holes are at height (H/3)and(2H/3) from the surface of water. Find the correct option(s):
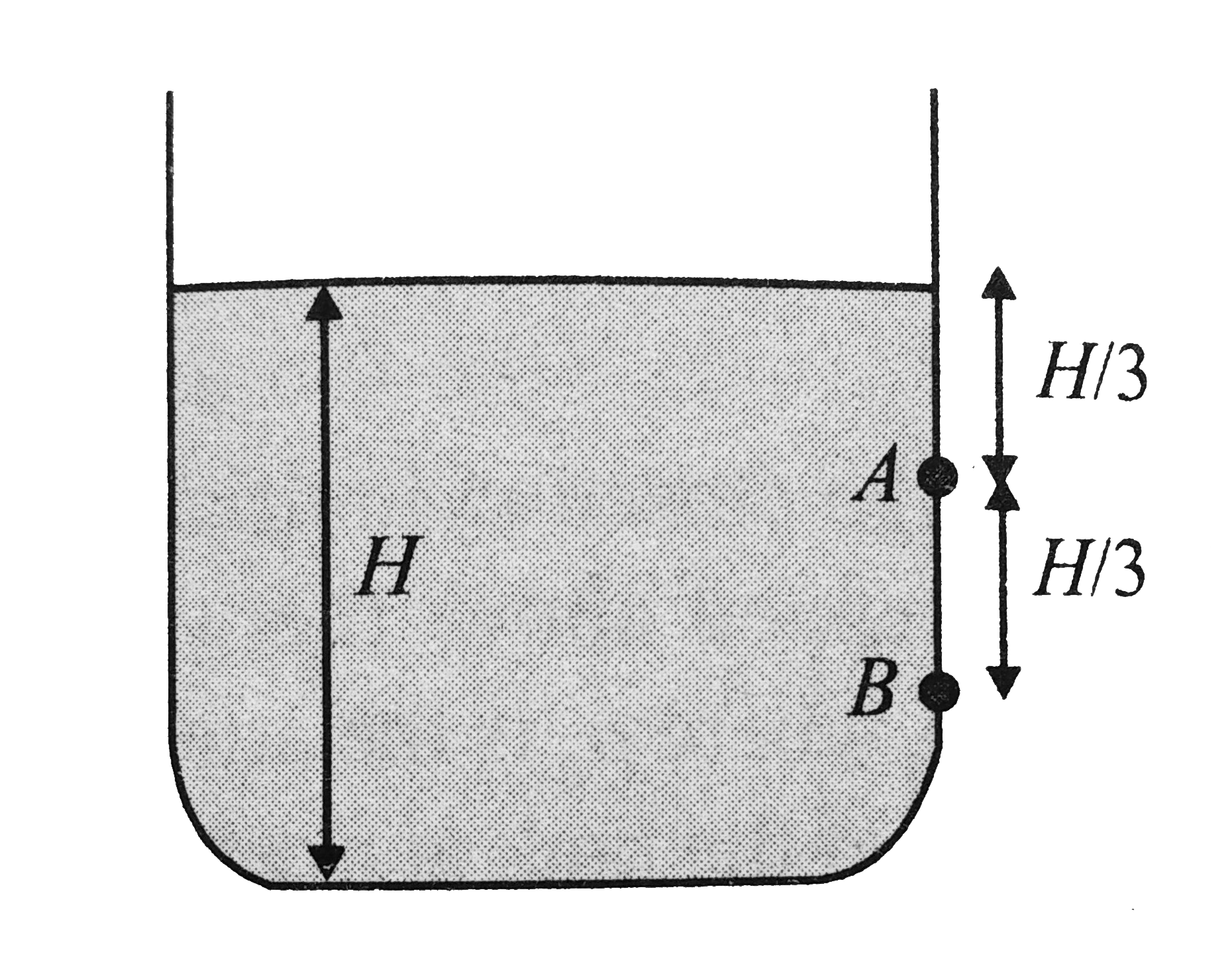 AThe velocity of efflux at hole B is 2 times the velocity of efflux at hole A.BThe velocity of efflux at hole B is √2 time the velocity of efflux at hole A.CThe discharge is same through both the holes.DThe discharge through hole A is √2 time the discharge through hole B.
AThe velocity of efflux at hole B is 2 times the velocity of efflux at hole A.BThe velocity of efflux at hole B is √2 time the velocity of efflux at hole A.CThe discharge is same through both the holes.DThe discharge through hole A is √2 time the discharge through hole B.Two trains of same length take 6 s and 9 s,respectively to cross a pole .If both the trains are running in the same direction, then how long will they take to cross each other?
Aa. 30sBb. 36sCc. 40sDd. 42 s
two bodies A and B of equal masses are kept at heights of h and 2h respectively. What will be the ratio of their potential energies ?
View SolutionThe time period of two pendulums of same length oscillating on different planets A and B is 2 s and 3 s, respectively . The ratio of acceleration due to gravity on the two planets is _______
View SolutionThe speeds of two trains A and B are 42 km/h and 33 km/h, respectively. Length of train B is 3/2 times the length of A. Train A takes 50 s to cross train B, if they are moving in the same direction. How long will they take to cross each other if they are moving in opposite directions ?
View SolutionA solid sphere and a solid cylinder of same mass are rolled down on two inclined planes of heights h1andh2 respectively. If at the bottom of the plane the two objects have same velocities, then the ratio of h1:h2 is
View SolutionIf the base radii of two cylinders are in the ratio 3:4 and their heights are in the ratio 4: 9. then the ratio of their respective volumes is :
View Solution
