In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so tht the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure. Let the mas of each kid be 15 kg, the distance betweent eh points of the rod where the two kids hold it be 3.0 m and supose that teh rod rotates at the rate of 20 revolutions per minute. Find the force of fircton exerted by te rod on one of the kids.

The correct Answer is:A, B
d=3m
→r=1.5m
r=Distanceformthecentre→o≠ofthek<br>n=20 rev per min<br>=20/60=1/3 rev/sec<br>omega=2pin=(2pi)/3rad/sec <br>:. FirctioN/Al force F=mromega^2<br>=15xx(15)xx((2pi)^2)/9<br>=5xx(0.5)x4pi^2=10pi^2<br>:. Friction force on one of the kids is 10π2.
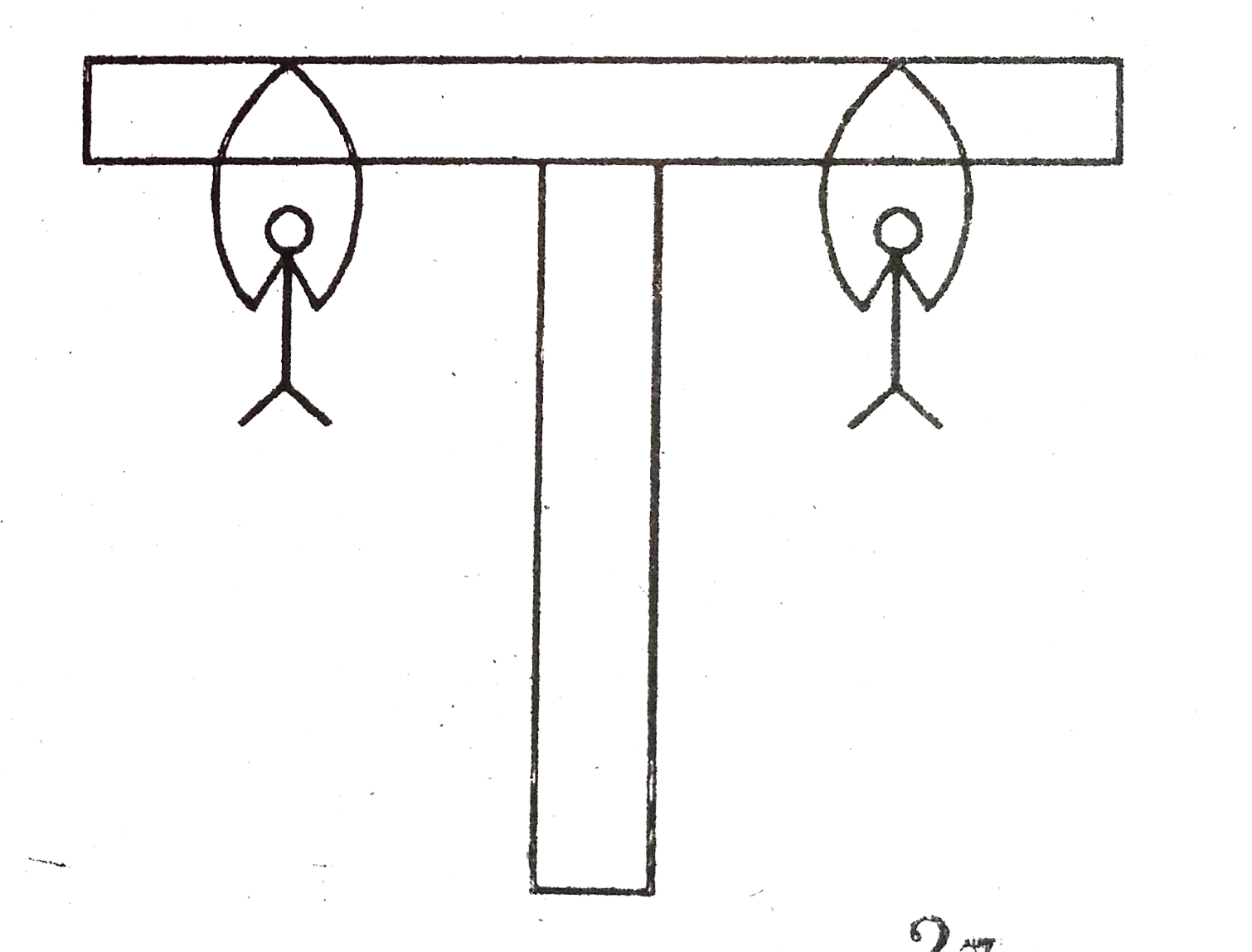
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 27videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises64videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises35videos
FLUID MECHANICS
Similar Questions
A rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View SolutionA uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
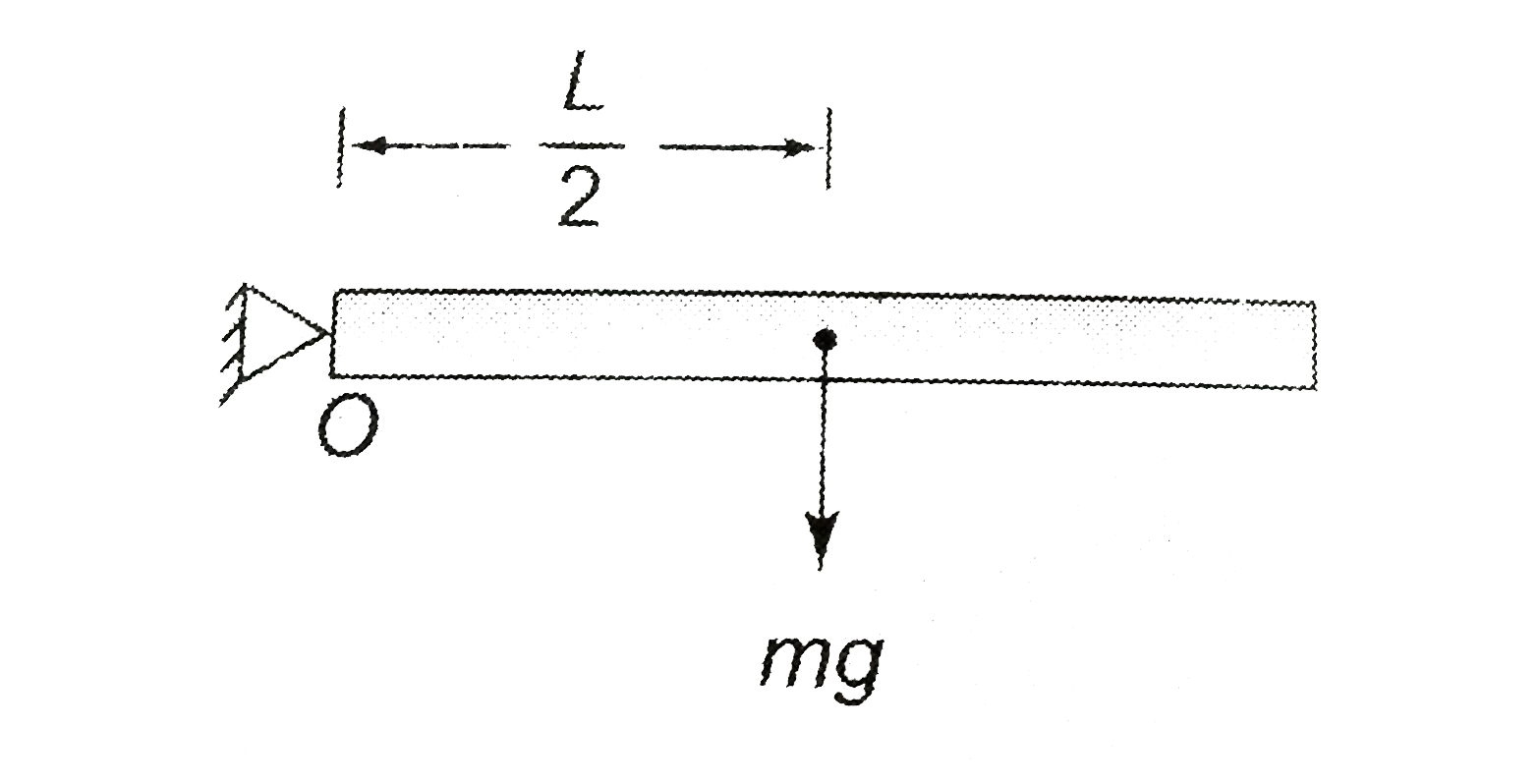 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is m . The force exerted by the rod on the particle is →F , then:
AF≥mgBF is constantCThe angle between →F and horizontal plane decreases.DThe angle between →F and the rod decreases. - Question 2 - Select One or More
A thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v0 to the one end B of the rod. When it hits, it sticks to the rod, then :
 AMinimum value of v0 for the rod to rotate by an angle π2is2√gL .BAngular acceleration of the rod when the rod is horizontal is 9g8L .CForce applied by the axis on the rod in the horizontal state is 5mg/6 .Dfor a small velue of v0 the rod performes small oscillations with a period of 43π√lg
AMinimum value of v0 for the rod to rotate by an angle π2is2√gL .BAngular acceleration of the rod when the rod is horizontal is 9g8L .CForce applied by the axis on the rod in the horizontal state is 5mg/6 .Dfor a small velue of v0 the rod performes small oscillations with a period of 43π√lg - Question 3 - Select One
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is.
A2.5 mB1 mC1.5 mD2 m
A rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
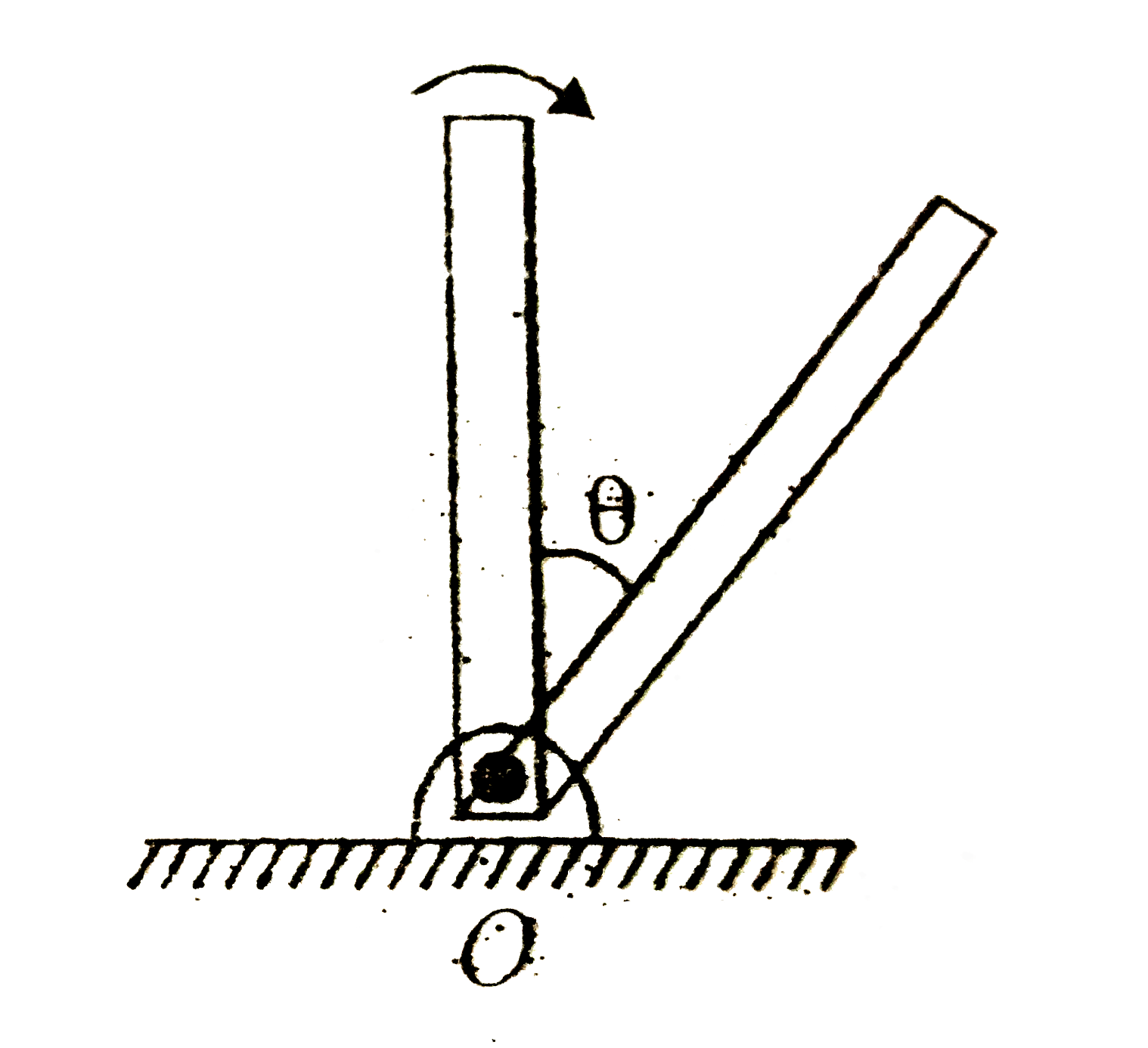 View Solution
View SolutionFigure shows a rigid rod of length 1.0 m. It is pivoted at O. For what value m, the rod will be in equilibrium ? Find the force (F) exerted on the rod by the pivot. Neglect the weight of the rod.
 View Solution
View SolutionA rod of length L is pivoted at one end and is rotated with as uniform angular velocity in a horizontal plane. Let T1andT2 be the tensions at the points L//4 and 3L//4 away from the pivoted ends.
View SolutionA rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View Solution

