In a constant , when the bob moves in a horizontal circle of radius r, with uniform speed v, the string of length L describes a cone of semivertical angle θ . The tension in the string is given by
T=mgL(L2−r2)
(L2−r2)1/2mgL
T=mgL√L2−r2
T=mgL(L2−r2)2
The correct Answer is:C
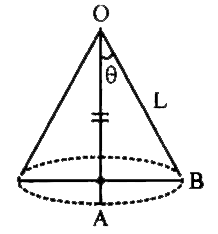
For a contal pendulum , the tension in the string is calculated by using Tcosθ=mg
From the figure cosθ=OAOB=√L2−r2L
∴T=mgcosθ=mg√L2−r2L=mgL√L2−r2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-1
1 Videos
- CIRCULAR MOTIONBOOK - MARVEL PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - TEST YOUR GRASP-2
1 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - MARVEL PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - TEST YOUR GRASP
30 Videos
- COMMUNICATION SYSTEMS BOOK - MARVEL PUBLICATIONCHAPTER - COMMUNICATION SYSTEMS EXERCISE - TEST YOUR GRASP -20
10 Videos
Similar Questions
A small block of mass m on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius r with speed v and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to r/2. (a) Find the tension in the string when the block moves in a circle of radius r/2. (b) Calculate the change in the kinetic energy of the block.

View SolutionA ball of mass m is suspended from a rope of length L. It describes a horizontal circle of radius r with speed v. the rope makes an angle θ with vertical given by sinθ=r/2. Determine (a) the tension in the rope and (b) the speed of the ball. (c) time period of ball.
View Solution
Knowledge Check
In a conical pendulam, when the bob moves in a horizontal circle of radius r with uniform speed v, the string of length L describes a cone of semivertical angle θ. The tension in the string is given by
AT=mgL√L2−r2BT=(L2−r2)1/2mgLCT=mgL(L2−r2)DT=mgL(L2−r2)2If a particle is moving in a circular path of radius 'r' with a uniform speed v, then the angle described by it in one second will be
Av rB1/vrCv/rDv/r2A particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point , its
AKinetic energy changes by MV2/4Bmomentum does not changeCMomentum changes by 2MVDkinetic energy changes by MV2
A particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point, its
View SolutionA stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View SolutionA stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
View Solutionbody is just being revolved in a vertical circle of radius R with a uniform speed. The string breaks when the body is at the highest point. The horizontal distance covred by the body after the string breaks is
View Solution
