In a free fall the velocity of a stone is increasing equally ion equal intervals of time under the effect of gravitational force of the earth. Then what can you say about the motion of this stone? Whether the stone is having:Solution in Tamil
-uniform acceleration
Non-uniform acceleration
retardation
constant speed
The correct Answer is:a
An object is in motion with initial velocity u attains a final velocity v in time t due to acceleration a, with displacement s.
Let us try to derive these equations by graphical method. Equations of motion from velocity-time graph:
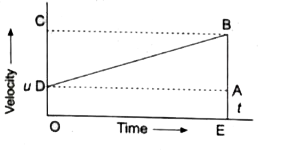
Graph shows the change in velocity with time for an uniformly accelerated object. The object starts from the point D in the graph with velocity u. Its velocity keeps increasing and after time t it reaches the point B on the graph .
The initial velocity of the object =u = OD = EA
The final velocity of the object =v=OC = EB
Time = t= OE = DA
Also from the graph we know that , AB=DC
For first equation of motion
By definition, acceleration =change in velocity / time
=(final velcity -initial velocity ) / time
=(OC-OD)/OE=DC/OE
a=DC/t
DC=AB=at
From the graph EB=EA+AB
v=u+at ....(1)
This is first equation of motion.
For second equation of motion
From the graph the distance covered by the object during time t is given by the area of quadrangle DOEB
s=area of the quad-rectangel DOEB
s=area of the rectangle DOEA + area of the triangle DAB
=(AE x OE) + (1/2 x AB x DA)
s=ut+1/2at2. ...(2)
This is second equation of motion.
For Third equation of motion
From the graph the distance covered by the object during time t is given by the area of the quadrangle DOEB . Here DOEB is a trapezium . Then
s=area of trapezium DOEB
=1/2 x sum of length of parallel side x distance between parallel sides
=1/2 x (OD +BE) x OE
s=1/2 x (u+v) x t
since a =(v-u)/t or t=(v-u)/a
Therefore s=1/2 x (v+u) x (v-u)/a
2as=v2−u2
v2=u2+2as ....(3)
This is third equation of motion.
Topper's Solved these Questions
- MOTIONBOOK - FULL MARKSCHAPTER - MOTIONEXERCISE - Question Paper -II (Choose the best answer )
2 Videos
- MOTIONBOOK - FULL MARKSCHAPTER - MOTIONEXERCISE - Question Paper -II (Choose correct statement )
1 Videos
- MOTIONBOOK - FULL MARKSCHAPTER - MOTIONEXERCISE - Question Paper -I (Short Answer )
5 Videos
- MAGNETISM AND ELECTROMAGNETISMBOOK - FULL MARKSCHAPTER - MAGNETISM AND ELECTROMAGNETISMEXERCISE - ACTIVITY
1 Videos
- SOUNDBOOK - FULL MARKSCHAPTER - SOUNDEXERCISE - ADDITIONAL QUESTIONS (Answer the following questions)
8 Videos
Similar Questions
In a 100 m race, the winner takes 10s to reach the finishing point. The average speed of the winner is ______ ms−1
View SolutionThe numerical ratio of displacement to distance for a moving object is:
View SolutionA bus travels, a distance of 20 km from Chennai central to airport in 45 minutes. What is the average speed?
View SolutionPut a magnet on a table and place some paper clips nearby . If you push the magnet slowly towards the paper clips there will be a point at which the paper clips jump across and stick to the magnet .what do you understand from this ?
View Solution"Sound needs a medium for propagation". Justify with an experiment.
View SolutionA stone falling towords earths also attractst the earth with the same force, Is it true ?
View SolutionA stone is dropped from a height equal to nR , where R is the radius of the earth, from the surface of the earth. The velocity of the stone on reaching the surface of the earth is
View SolutionA stone is dropped from a height equal to 3R , above the surface of earth. The velocity of stone on reaching the earth's surface is
View SolutionA stone and the earth attract each other with an equal and opposite force.Why then we see only the stone falling towards the earth but but not the earth rising towards the stone ?
View SolutionAlong a road lies an odd number of stones placed at intervals of 10m. These stones have to be assembled around the middle stone. A person can carry only one stone at a time. A man carried out the job starting with the stone in the middle, carrying stones in succession, thereby covering a distance of 4.8 km. Then the number of stones is
View Solutionयदि पृथ्वी के व्यास के अनुदिश सुरंग बनाकर उसमे पत्थर छोड़ दे , तो पत्थर :
View SolutionTake a small stone. Hold it in your hand. What are the forces acting on the stone ? Now release the stone. What do you observe ? What are the forces acting on the stone after you release it ?
View SolutionTake a small stone. Hold it in your hand. What are the forces acting on the stone ? Now release the stone. What do you observe ? What are the forces acting on the stone after you release it ?
View SolutionA stone is falling freely. The distance travelled in the last second is equal to that travelled in the first three seconds. The time spent by the stone in air is
View Solutionएक पत्थर स्थिर अवस्था से स्वतंत्र रूप से गिर रहा है। इसके द्वारा गति के अंतिम सेकण्ड में चली गयी दुरी, गति के पहले तीन सेकण्ड में चली गयी गई दुरी के बराबर है। पत्थर वायु में रहा
View SolutionAccording to Newton.s third law of motion, if the earth pulls a stone, the stone must also pull the earth. Then why doesn.t the earth fall towards the stone ?
View Solution
