In a particular fission process of atom at rest Fragents with mass number and are produced. Then find ratio of kinetic energies of the fragments?
The correct Answer is:A
To find the ratio of kinetic energies of the fragments produced in a fission process, we can follow these steps:
Step 1: Understand the Conservation of Momentum
In a fission process, the total momentum before and after the fission must be conserved. Since the original atom is at rest, its initial momentum is zero. Therefore, the momentum of the two fragments after fission must also sum to zero.
Step 2: Set Up the Momentum Equation
Let the mass numbers of the two fragments be A1 and A2, and their velocities be V1 and V2 respectively. According to the conservation of momentum:
A1V1+A2V2=0
This implies:
A1V1=−A2V2
Taking the magnitudes, we have:
A1V1=A2V2
From this, we can express the ratio of the velocities:
V1V2=A2A1
Step 3: Write the Kinetic Energy Expressions
The kinetic energy (KE) of each fragment can be expressed as:
KE1=12A1V21
KE2=12A2V22
Step 4: Find the Ratio of Kinetic Energies
Now, we can find the ratio of the kinetic energies:
KE1KE2=12A1V2112A2V22=A1V21A2V22
The 12 cancels out, so we simplify to:
KE1KE2=A1V21A2V22
Step 5: Substitute the Velocity Ratio
Using the ratio V1V2=A2A1, we can substitute V1 in terms of V2:
V1=A2A1V2
Now substituting this into the kinetic energy ratio:
KE1KE2=A1(A2A1V2)2A2V22
This simplifies to:
KE1KE2=A1A22A21V22A2V22=A2A1
Final Answer
Thus, the ratio of the kinetic energies of the fragments is:
KE1KE2=A2A1
In a fission process, the total momentum before and after the fission must be conserved. Since the original atom is at rest, its initial momentum is zero. Therefore, the momentum of the two fragments after fission must also sum to zero.
Let the mass numbers of the two fragments be A1 and A2, and their velocities be V1 and V2 respectively. According to the conservation of momentum:
A1V1+A2V2=0
This implies:
A1V1=−A2V2
Taking the magnitudes, we have:
A1V1=A2V2
From this, we can express the ratio of the velocities:
V1V2=A2A1
The kinetic energy (KE) of each fragment can be expressed as:
KE1=12A1V21
KE2=12A2V22
Now, we can find the ratio of the kinetic energies:
KE1KE2=12A1V2112A2V22=A1V21A2V22
The 12 cancels out, so we simplify to:
KE1KE2=A1V21A2V22
Using the ratio V1V2=A2A1, we can substitute V1 in terms of V2:
V1=A2A1V2
Now substituting this into the kinetic energy ratio:
KE1KE2=A1(A2A1V2)2A2V22
This simplifies to:
KE1KE2=A1A22A21V22A2V22=A2A1
Thus, the ratio of the kinetic energies of the fragments is:
KE1KE2=A2A1
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE LEVEL-II (LECTURE SHEET (ADVANCED)) Straight Objective Type Questions )
9 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE LEVEL-II (LECTURE SHEET (ADVANCED)) More than one correct answer Type Questions )
4 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - PRACTICE SHEET Matrix Matching Type Questions
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
- NUCLEIBOOK - AAKASH SERIESCHAPTER - NUCLEIEXERCISE - Practice Exercise
40 Videos
Similar Questions
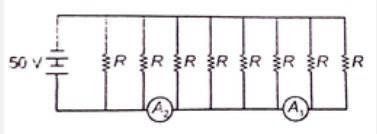
In the situation shown , the readings of ideal ammeters A1 and A2 are in the ratio.
View SolutionA neutron collides head-on and elasticity with an atom of mass number A, which is initially at rest. The fraction of kinetic energy retained by neutron is
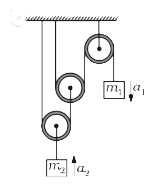
View SolutionFind the relation between acceleration a1 and a2
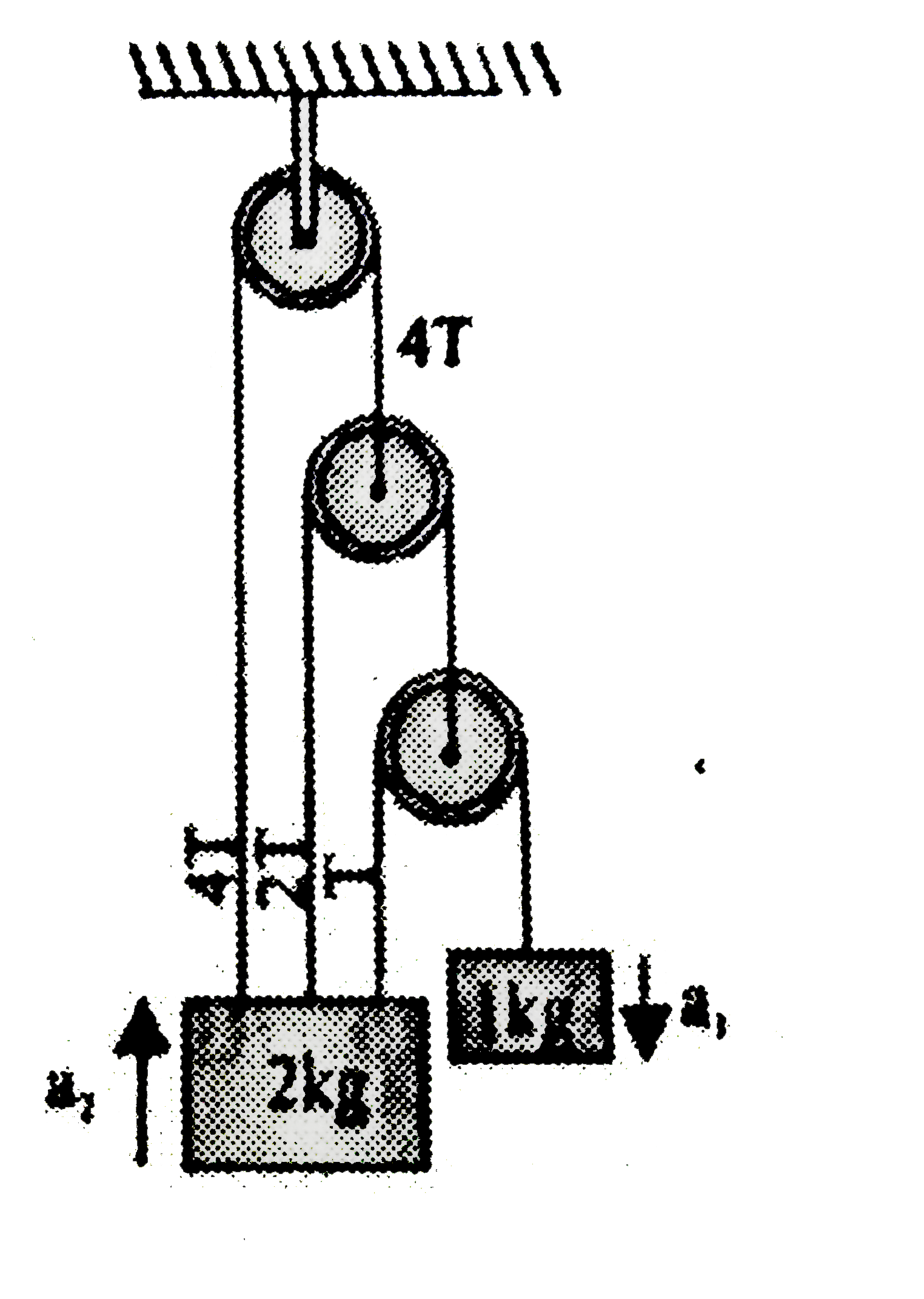
View SolutionUsing contraint equation. Find the relation between a1anda2.
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View SolutionIn the fission of .23994Pu by a thermal neutron, two fission fragmnets of equal masses and sizes are produced and four neutrosn are emitted. Find the force between the two fission fragments at the moment they are produced.
Given : R0=1.1 fermi.
View SolutionA stationary shell explodes into two fragments, having masses in the ratio of 1:2. The heavier fragment attains a Kinetic energy of 100J. The Kinetic energy released in the explosion is:
View SolutionUsing constraint method find the relation between of a1 and a2.

View SolutionIn an interference experiment the ratio of amplitudes of coherent waves is a1a2=13. The ratio of maximum and minimum intensities of fringes will be:
View Solution
