In an open ground, a motorist follows a track that turns to his left by an angle 600 after every 200m. Starting from a given turn, covered at the ceons, and the total path turn.
To solve the problem, we need to analyze the motion of the motorist who turns left by an angle of 60∘ after every 200m. We will calculate the distance covered, the displacement at the end of the second turn, and the total path length.
1. Understanding the Path:
- The motorist starts from point A and moves 200m to point B.
- From point B, he turns left 60∘ and moves another 200m to point C.
2. Calculating the Displacement (AC):
- To find the displacement from point A to point C, we can use the cosine rule in triangle ABC.
- The angle at point B (between AB and BC) is 60∘.
- The lengths AB and BC are both 200m.
Using the cosine rule:
AC2=AB2+BC2−2⋅AB⋅BC⋅cos(60∘)
Substituting the values:
AC2=2002+2002−2⋅200⋅200⋅12
AC2=40000+40000−40000
AC2=40000
AC=√40000=200√3 m
3. Calculating the Total Distance:
- The total distance covered after the second turn is simply the sum of the distances AB and BC.
Distance=AB+BC=200m+200m=400m
4. Calculating the Total Path Length:
- The motorist continues to turn left and move 200m for each turn. The total path length after completing the turns until he returns to point A can be calculated.
- After the first turn (B), second turn (C), third turn (D), fourth turn (E), fifth turn (F), and finally returning to A, he completes 6 segments of 200m.
Total Path Length=200m×7=1400m
Final Answers:
- Displacement (AC): 200√3 m
- Distance covered after second turn: 400 m
- Total path length: 1400 m
- The motorist starts from point A and moves 200m to point B.
- From point B, he turns left 60∘ and moves another 200m to point C.
- To find the displacement from point A to point C, we can use the cosine rule in triangle ABC.
- The angle at point B (between AB and BC) is 60∘.
- The lengths AB and BC are both 200m.
AC2=AB2+BC2−2⋅AB⋅BC⋅cos(60∘)
Substituting the values:
AC2=2002+2002−2⋅200⋅200⋅12
AC2=40000+40000−40000
AC2=40000
AC=√40000=200√3 m
- The total distance covered after the second turn is simply the sum of the distances AB and BC.
Distance=AB+BC=200m+200m=400m
- The motorist continues to turn left and move 200m for each turn. The total path length after completing the turns until he returns to point A can be calculated.
- After the first turn (B), second turn (C), third turn (D), fourth turn (E), fifth turn (F), and finally returning to A, he completes 6 segments of 200m.
Total Path Length=200m×7=1400m
- Displacement (AC): 200√3 m
- Distance covered after second turn: 400 m
- Total path length: 1400 m
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 SolvedExamples31videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Conceptual Problems2videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 SolvedExamples31videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
On an open graound , a motor ist follws a track that truns to his left by an angle of 60∘ after every 500m. Starting from a given trun , specify the displacement of the motorist at the third, sizth and eighth turn. Compare the magniude of the dispalcembt with total path length coverd by the motorist in each case.
View SolutionA cyclist moves in such a way that he takes 600 turn after every 100 metres. What is the displacement when he takes seventh turn?
View Solution
Knowledge Check
- Question 1 - Select One
On an open ground, a motorist follows a track that turns to his left by an angle of 60∘ after every 500m. Starting from a given turn, The path followed by the motorist is a regular hexagon with side 500m, as shown in the given figure specify the displacement of the motorist
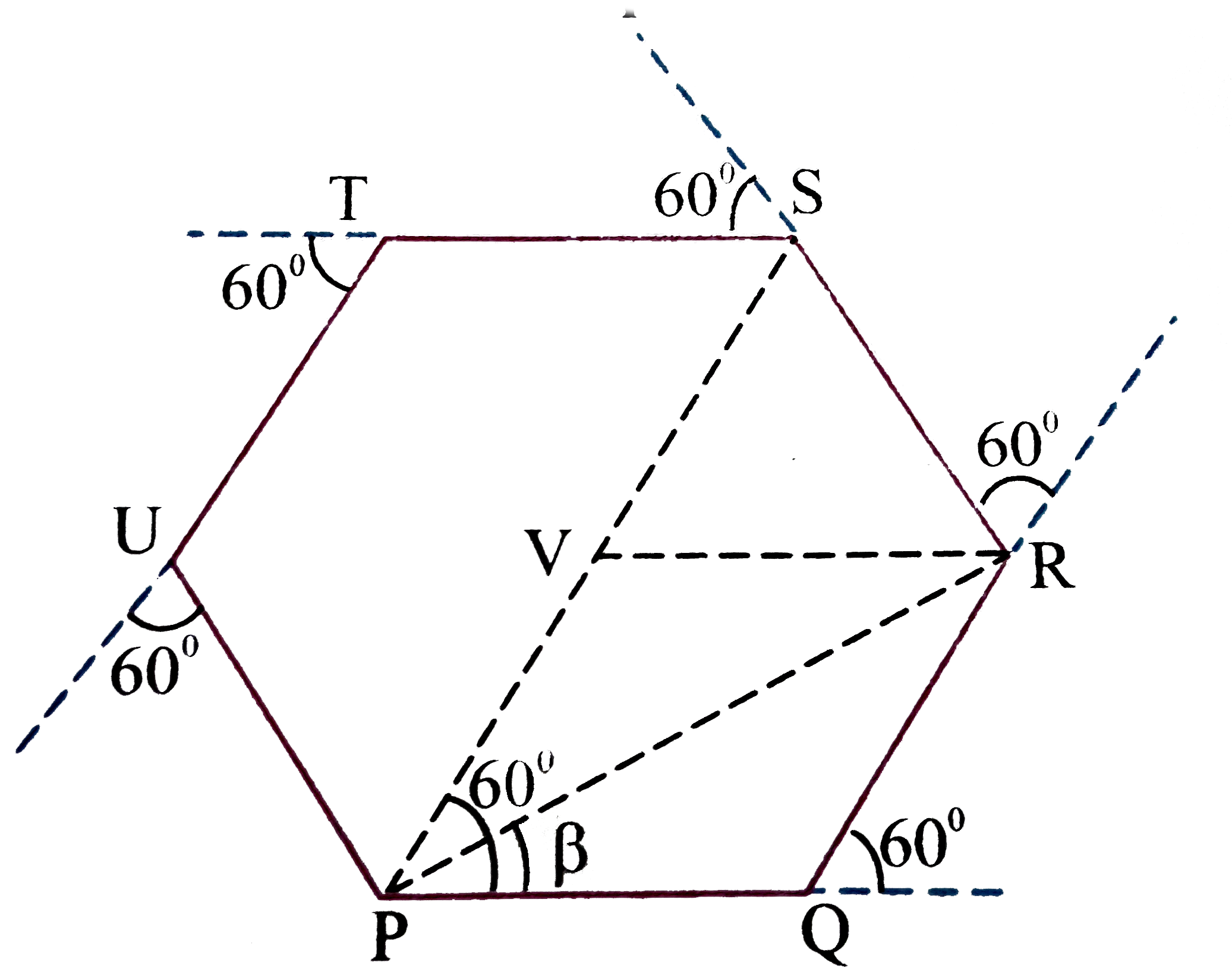
at the end of third turn.A500mB250mC1000mD1500m - Question 2 - Select One
On an open ground, a motorist follows a track that turns to his left by an angle of 60∘ after every 500m. Starting from a given turn, The path followed by the motorist is a regular hexagon with side 500m, as shown in the given figure specify the displacement of the motorist

at the end of sixth turn.A3000mB1500mC0mD1000m - Question 3 - Select One
On an open ground, a motorist follows a track that turns to his left by an angle of 60∘ after every 500m. Starting from a given turn, The path followed by the motorist is a regular hexagon with side 500m, as shown in the given figure specify the displacement of the motorist

at the end of eighth turn.A3000mB1500mC0mD866m
Arjun starts moving in the east direction. After running 50 meters, he turns his left and walks 15 meters straight. Then, from there, he turns to his left and walks 30 meters straight. He again turns 15 turns to his left. How far is he from the starting point ?
View SolutionArjun starts walking towards the east, after walking 50 Km he turns to his left and walks 15 m. From there he again turns to the left and walk 30m. Finally he turns to the left one last time and walk 15 m. How far is he from the starting point?
View SolutionGaurav starts walking in the North direction and travels 5 km then he turns to his left and walks 10 km and then he turns to his left and covers the distance of 5 km. Now how far is he from his starting point ?
View SolutionRam started walking from his office and covers 5 km then he turn to his left and covers 8 km and then turns to his right and covers 8 km Finaly turns to his left and covers 3 km and observe that at last he was going towards south direction. Find out towards which direction he started walking?
View SolutionAfter going 80 m from his house towards east, a person turns left and goes 20 m, then turns right and moves 100 m, then turns left and goes 60 m, then turns left and goes 120m to reach the park. What is the distance between his house and the park?
View Solution

