IN fig, calculate the total flux of the electrostatic field through the spheres . The wire AB shown here has a linear charge density . Given by , where x is the distance measured along the wire from end A.
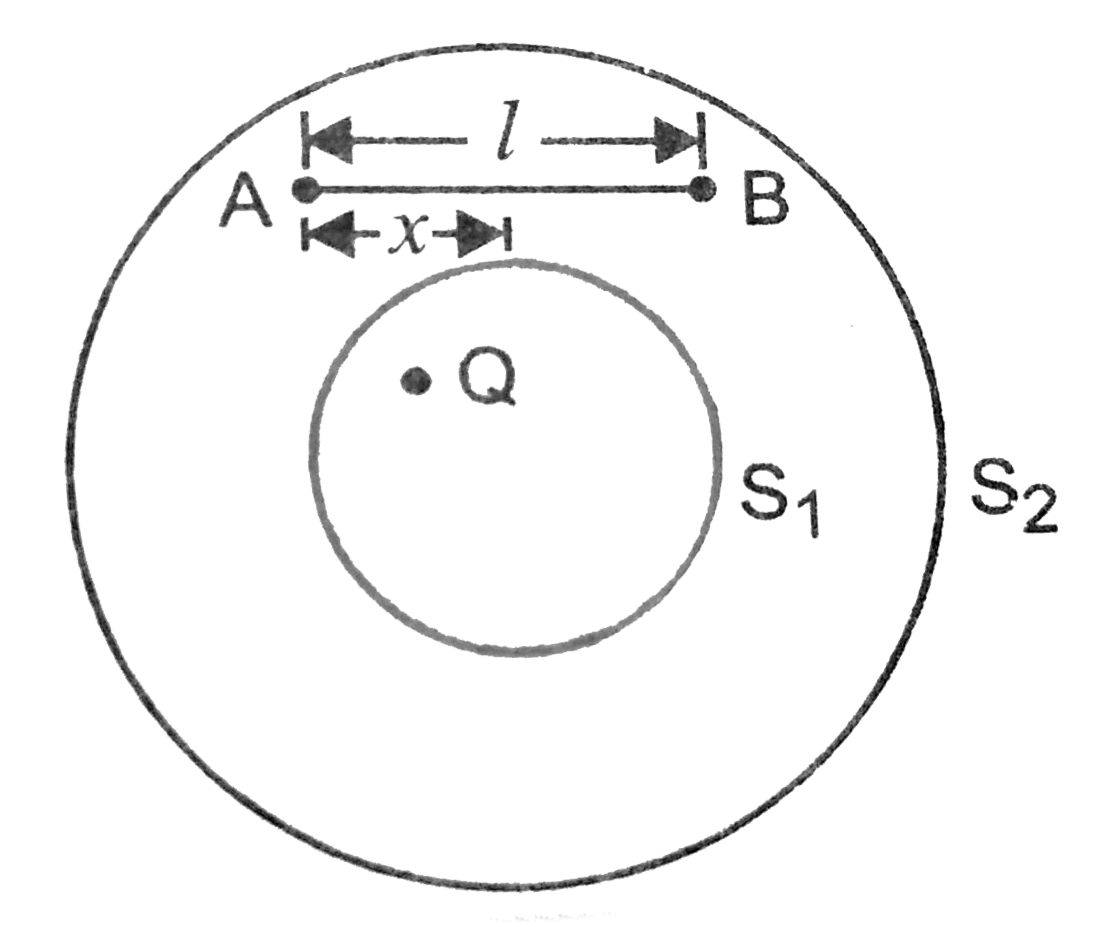
Charge on an element of length dx of wire AB
Total charge on wire AB,
Total flux through
Total flux through
Similar Questions
In the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
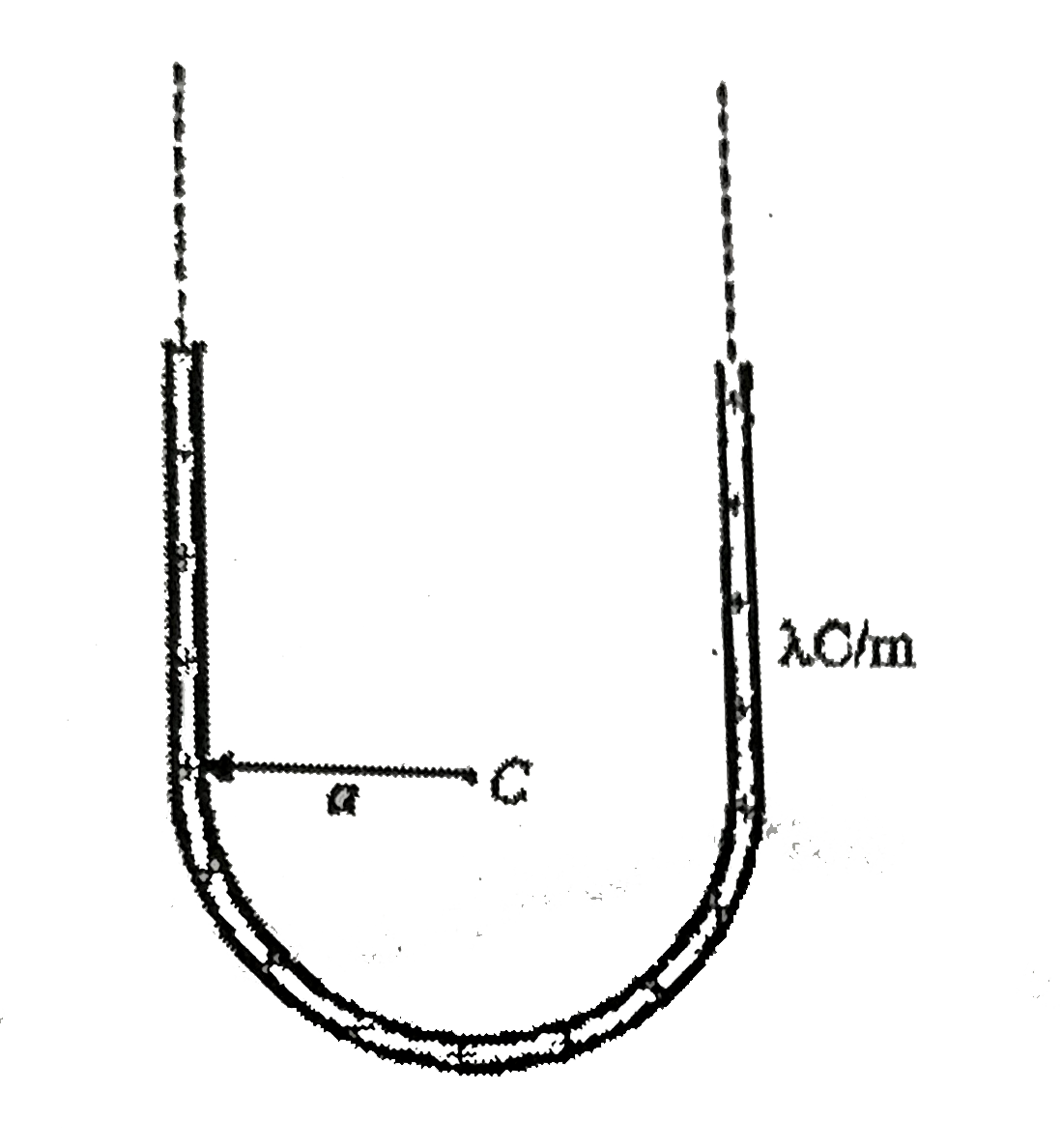
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View Solution
Knowledge Check
A charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
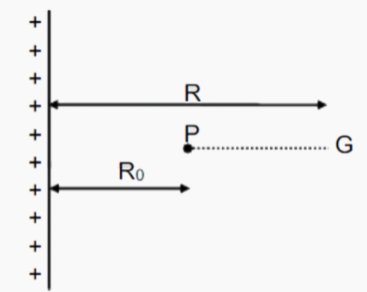 AR3BeR/R0CR2D[n(RR0)]−1/2
AR3BeR/R0CR2D[n(RR0)]−1/2An insulated sphere of radius R has a uniform volume charge density λ. The electric field at a point A, which is at distance r from its center is given by (R>r)
AZeroBRλ/3∈0C2rλ3∈0Drλ3∈0
(a) State Gauss's law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge desntiy λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionState Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ
(ii) A wire AB of length L has linear charge λ=kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.
View SolutionObtain the formula for the electric field due to a along thin wire of uniform linear charge density λ without using Gauss's law.
View SolutionA circular wire of radius r has a uniform linear charge density λ=λ0cos2θ, The total charge on the wire is απλ0r2 Find α.
View SolutionA horizontal rod AB of length 1 is rotated with constant angular velocity ω about a vertical axis passing through end A. A non-uniform charge of the linear charge density λ=λ0x is distributed on the rod where x is the distance from the end A and λ0 is a constant.Find the ratio of the energy desity of magnetic field and electric field on the vertical line passing through A, at a point whose distance is 1 from the end A.
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View Solution
