In the arrangement shown in figure, the rod of mass mhelp by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.

Let acceleration of m be a1 (absolute) and that of M be a2 (absolute).
Writing equations of motion only in the direction of a1 ora2
For mmgcosα−N=ma1 …(i)
For M. Nsinα=ma1 …(ii)
Here N= normal reation between m and M
As discussed above, constraint rquation can be written as,
a1=a2sinα ...(iii)
Solving above three equation, we get
acceleration of rod a1=mgcosαsinα(msinα+Msinα)
and acceleration of wedge a2=mgcosαmsinα+Msinα
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples9videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.110videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
In the arrangement shown in figure, the rod of mass m held by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 View Solution
View SolutionIn the shown arrangement , both pulleys and the string are massless and all the surface are frictionless. Find the acceleration of the wedge.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
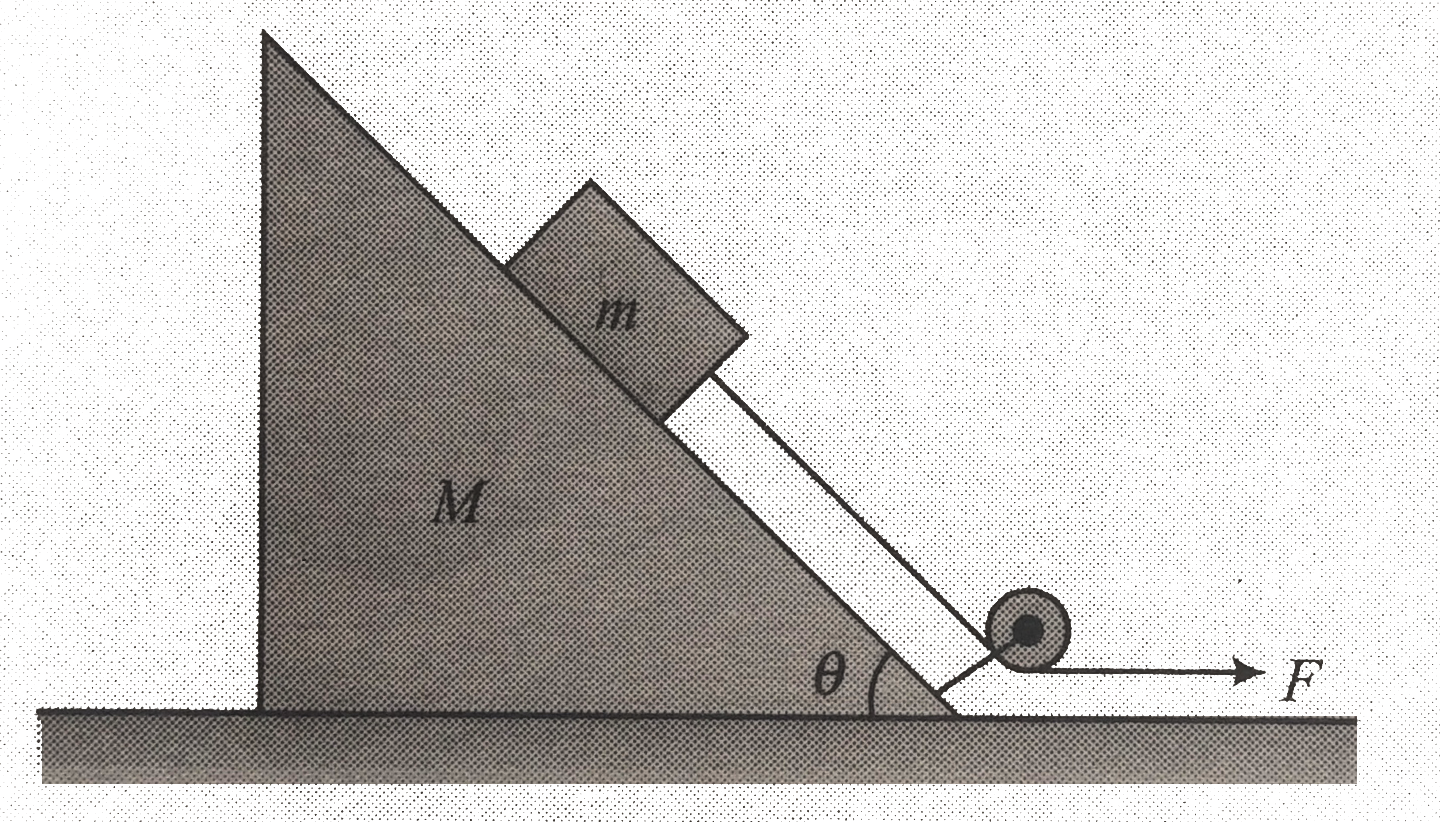 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ - Question 2 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
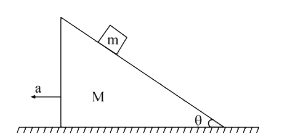 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ - Question 3 - Select One
All surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
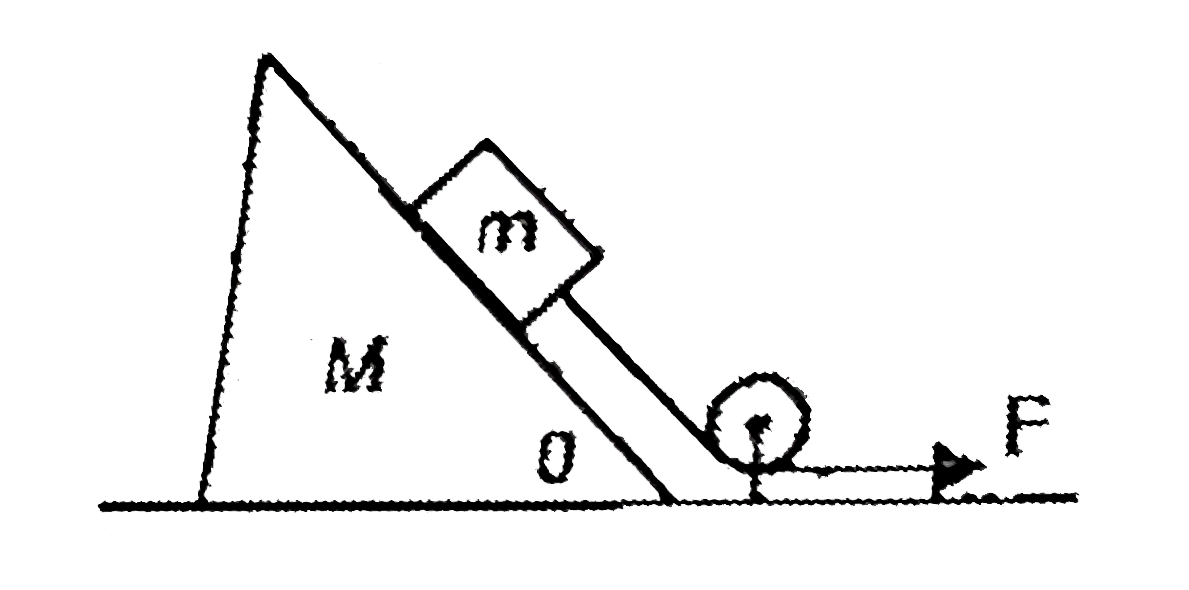 View Solution
View SolutionIn the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
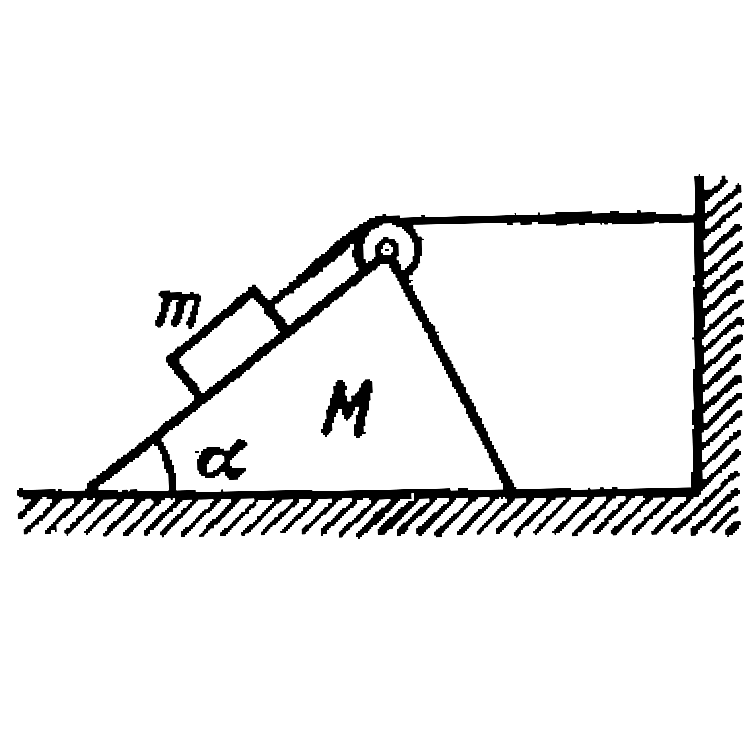 View Solution
View SolutionIn the arrangement shown in figure-2.68 the masses of the wedge M and the body m are known. There is no friction at any of the surfaces. The mass of the pulleys and thread is negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.
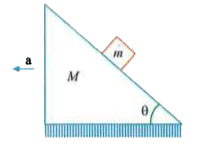
[√2mgM+2m]View SolutionIn the arrangement shown in figure wedge of mass M moves towards left with an acceleration a. All surfaces are smooth. The acceleration of mass m relative to wedge is
 View Solution
View SolutionAll surfaces are smooth. The acceleration of mass m relative to the wedge is
 View Solution
View Solution

