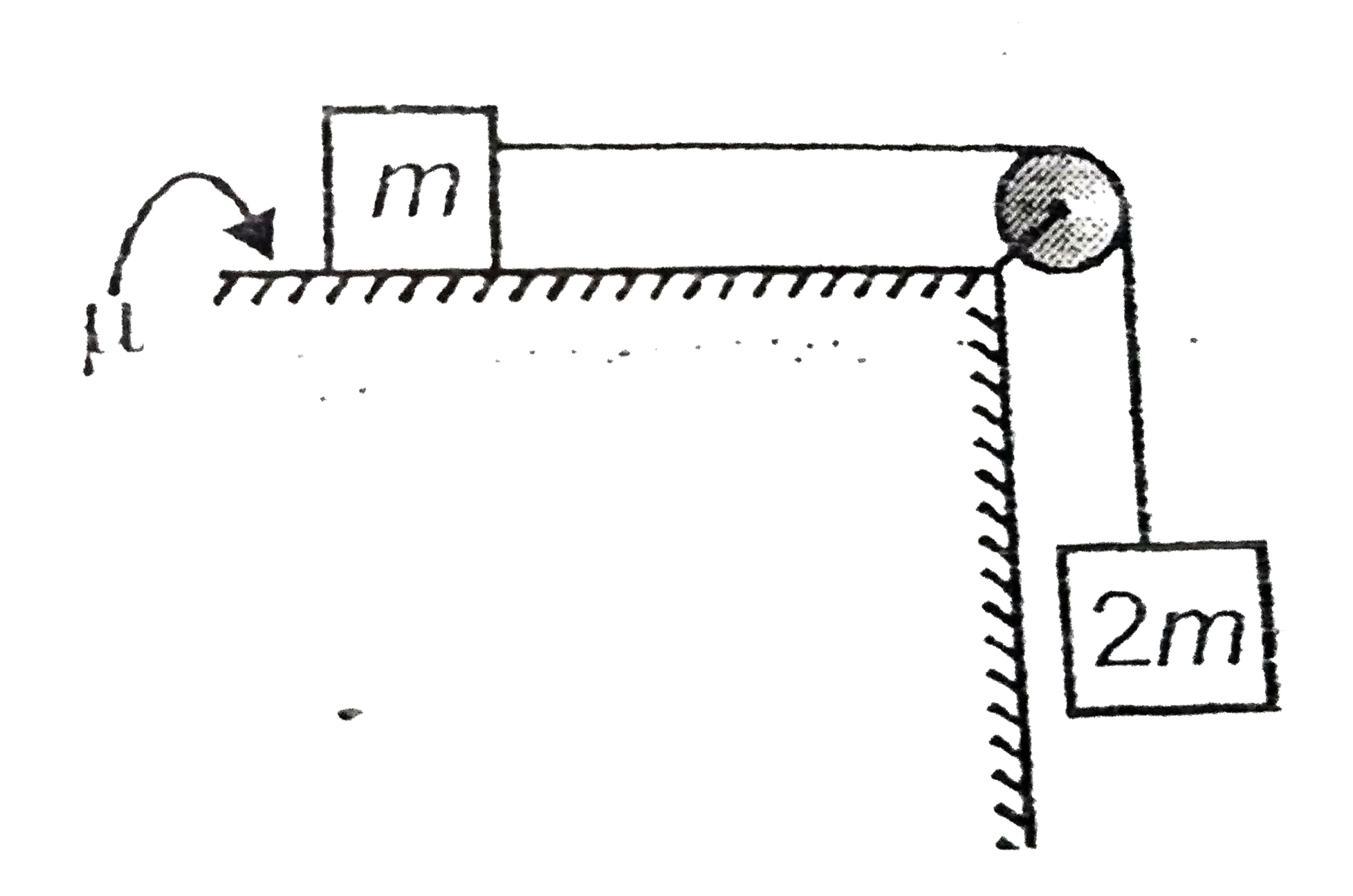
In the arrangment shown in figure, mA=1 kg, mB=4 kg. String is light and inextensible while pulley is smooth. Coefficient of friction between block A and the table is μ=0.2. Find the speed of both the blocks when block B has descended a height h=1 m. (Take ,g=10 ms−2)
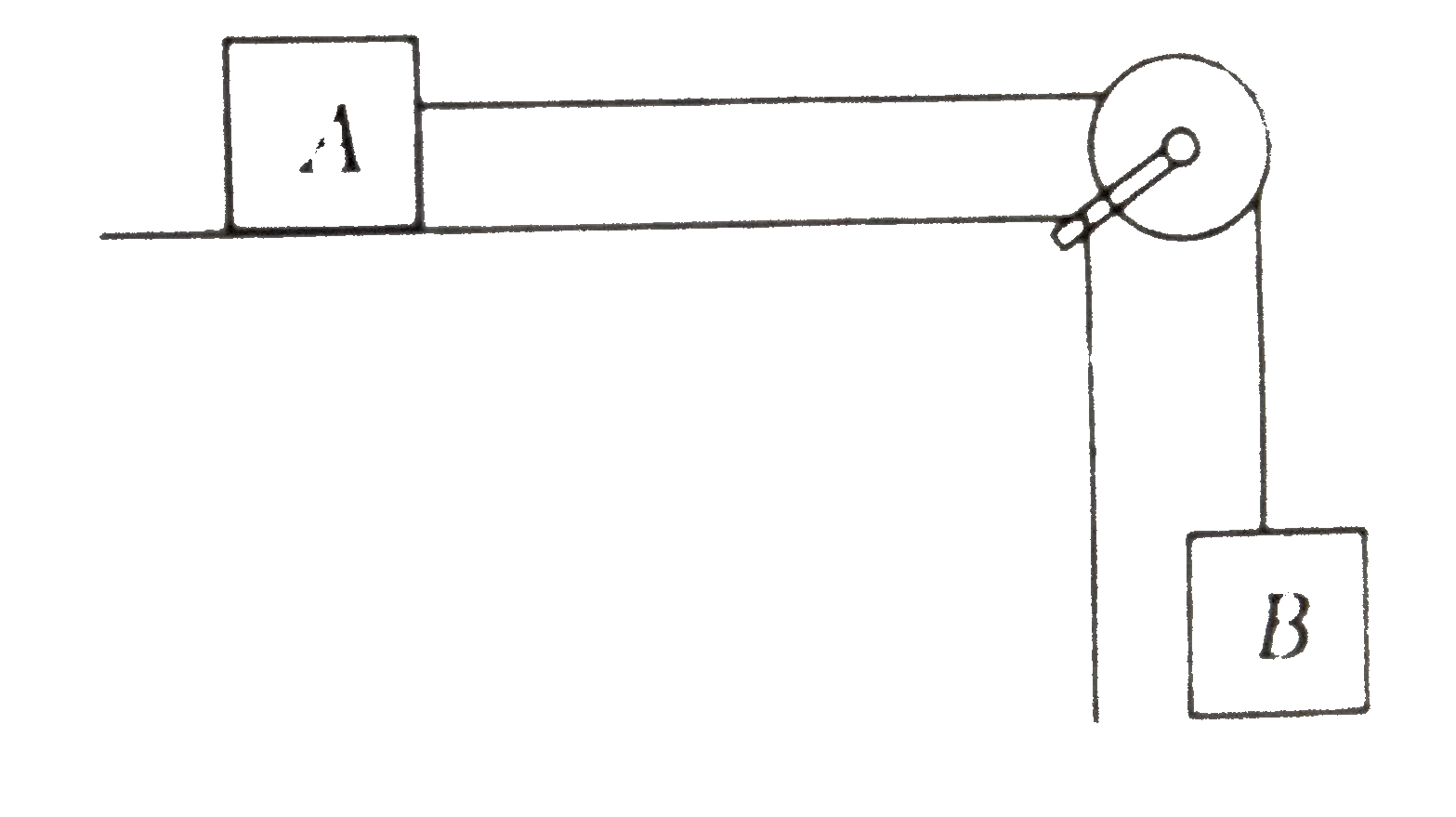
From constraint relation, we see that
vA=vB=v
Force of friction between block A and table will be
f=μmAg=(0.2)(1)(10)=2N
∴Wnc=ΔU+ΔK
∴−fs=−mBgh+(1/2)(mA+mB)v2
or (−2)(1)=−(4)(10)(1)+12(4+1)v2
−2=−40+2.5v2 or 2.5v2=38
∴v2=15.2m2s−2 or v=3.9ms−1
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.1
20 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.2
20 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
In the arrangement shown in Figure, mA=2kg and mB=1kg. String is light and inextensible. Find the acceleration of centre of mass of both the blocks. Neglect friction everywhere.

View SolutionIn the arrangement shown in figure pulley P can move whereas other two pulleys are fixed. All of them are light. String is light and inextensible. The coefficient of friction between 2 kg and 3 kg block is μ=0.75 and that between 3 kg block and the table is μ=0.5. The system is released from rest
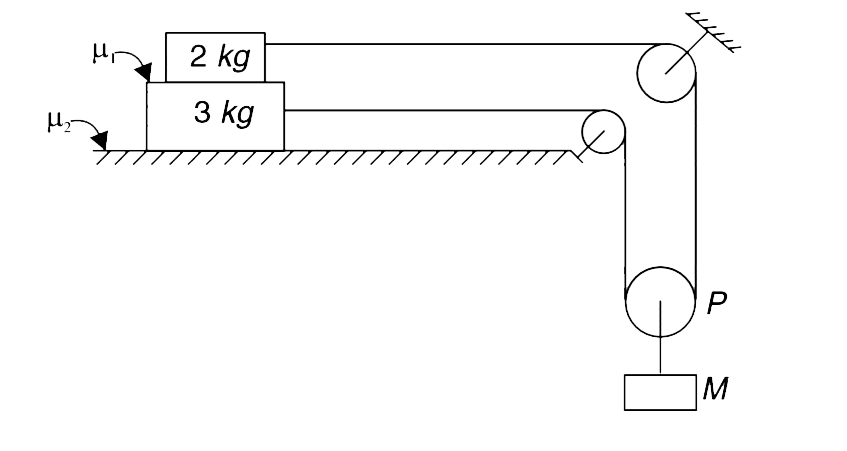
(i) Find maximum value of mass M, so that the system does not move. Find friction force between 2 kg and 3 kg blocks in this case.
(ii) If M = 4 kg, find the tension in the string attached to 2 kg block.
(iii) If M = 4 kg and μ1=0.9, find friction force between the two blocks, and acceleration of M.
(iv) Find acceleration of M if m1=0.75,m2=−0.9 and M = 4 kg.
View Solution
Knowledge Check
The coefficient of friction between 4 kg and 5 kg blocks is 0.2 and between 5 kg block and ground is 0.1 respectively. Choose the correct statement : (Take g=10m/s2)
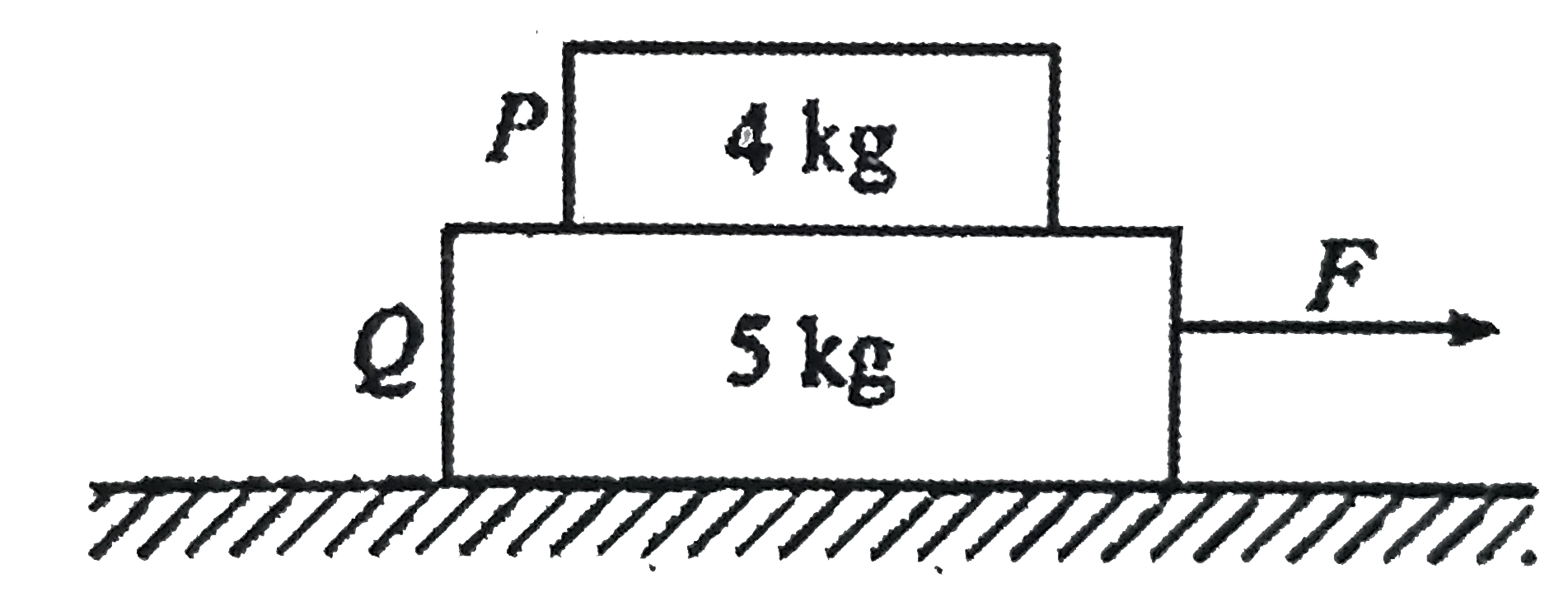 AMinimum force needed to cause system to move is 17 NBWhen force is 4 N static friction at all surfaces is 4 N to keep system at restCMaximum acceleration of 4 kg block is 2m/s2DSlipping between 4 kg and 5 kg blocks start when F is 17 N
AMinimum force needed to cause system to move is 17 NBWhen force is 4 N static friction at all surfaces is 4 N to keep system at restCMaximum acceleration of 4 kg block is 2m/s2DSlipping between 4 kg and 5 kg blocks start when F is 17 NIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NIn the arrangement shown in figure, string is light and inextensible and friction is absent every where. The speed of bothblocks after the block 'A' has ascend a height of 1m will be (g=10m/s2)
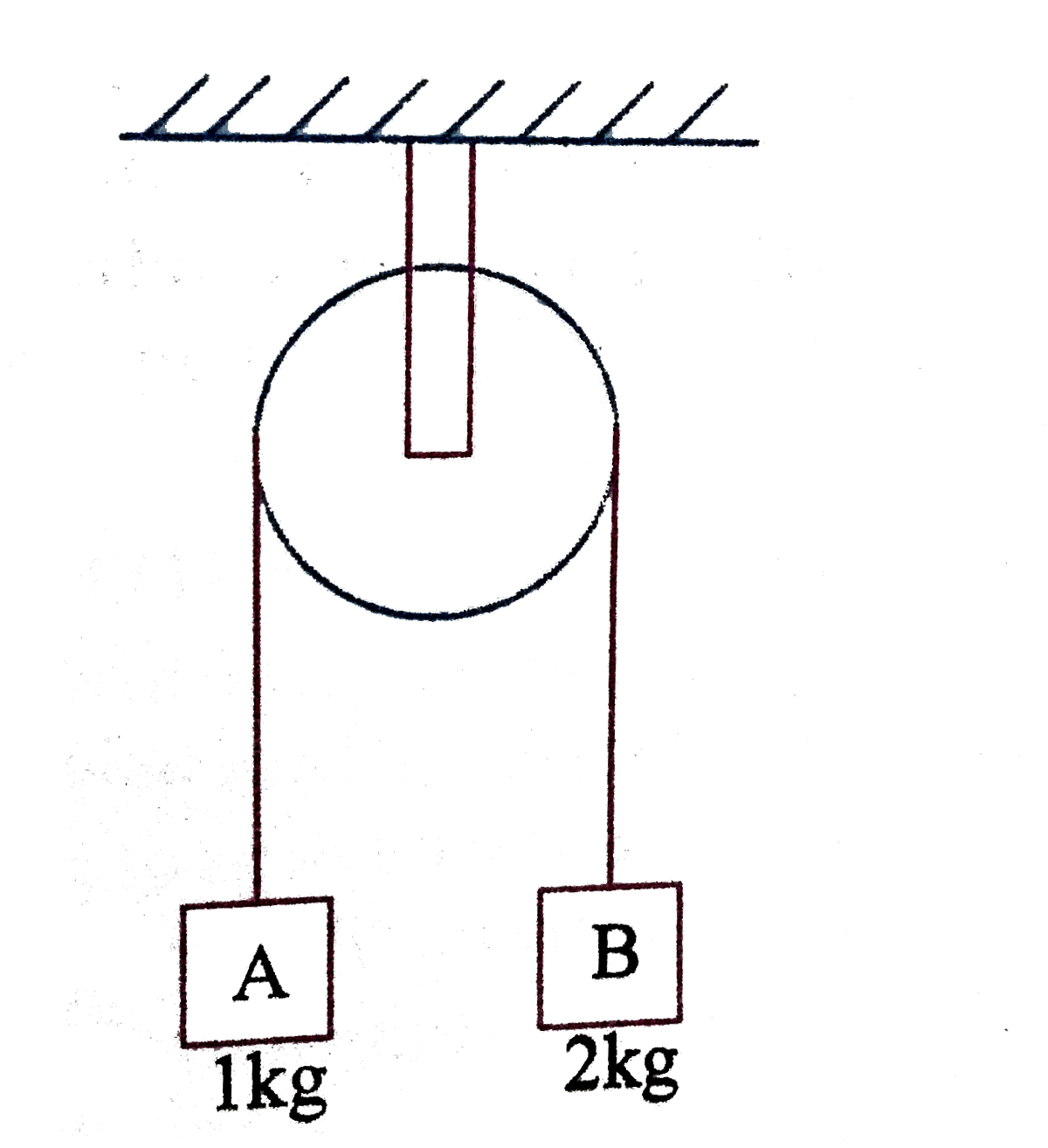 A2m/sB2.58m/sC3m/sD3.58m/s
A2m/sB2.58m/sC3m/sD3.58m/s
A force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionConsider the system shown in the figure. Coefficient of friction between the block and table is μ=0.5. The system is released from rest. Find the work done by friction, when the speed of block is 10 m/s (m=1kg)
View SolutionIn the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is μ=0.5 . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

View SolutionIn the arrangement shown in figure mA=mB=2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient between blocks A and B is μ=0.5. What maximum horizontal force F can be applied so that block A does not slip over the block B? (g=10m/s2)
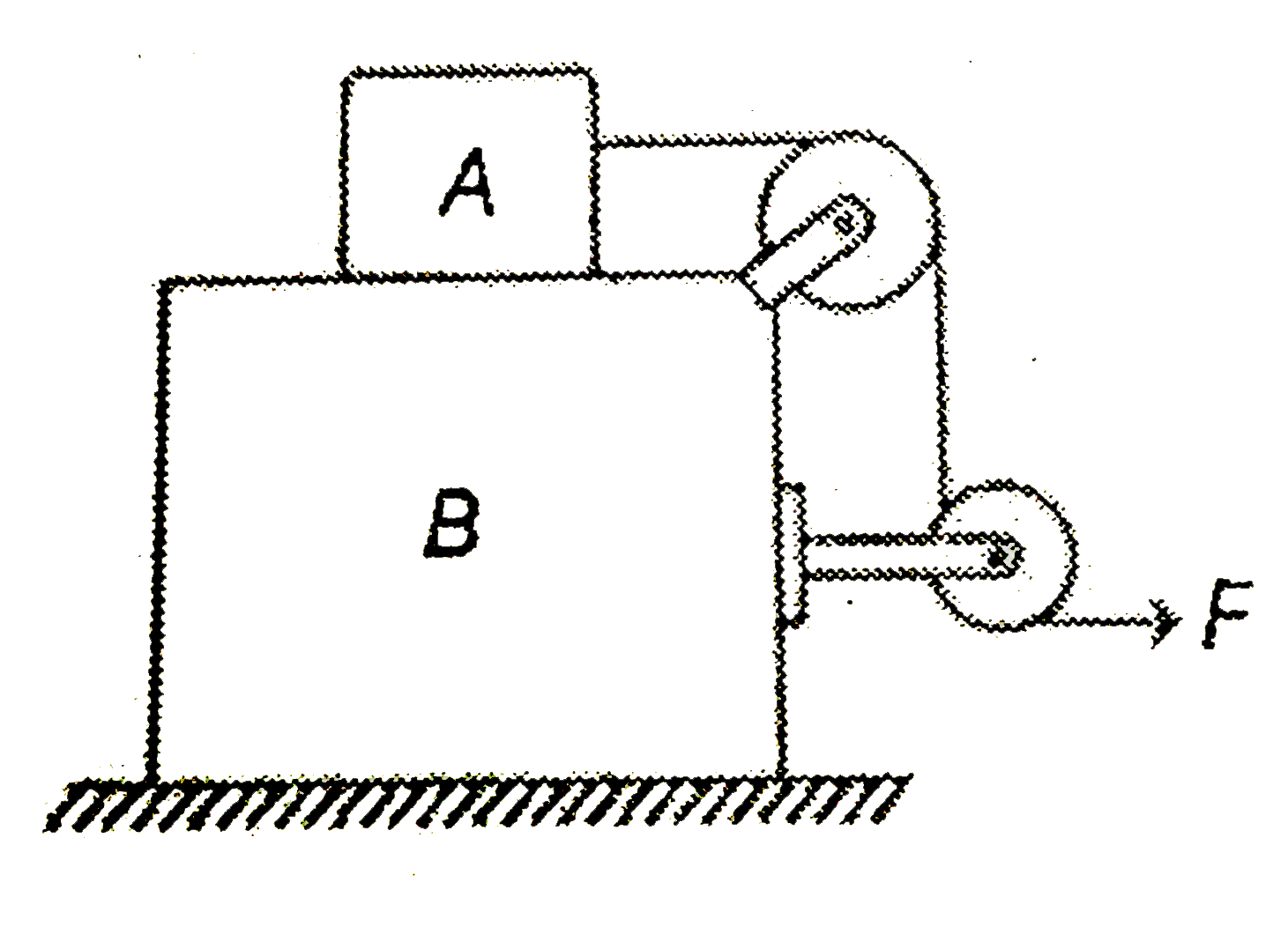
View SolutionA trolley of mass 20 kg is attached to a block of mass 4kg by massless string passing over a frictionless pulley as shown in the figure. If the coefficient of kinetic friction between trolley and the surface is 0.02, then the acceleration of the trolley and block system is (Takeg=10ms−2)

View Solution
