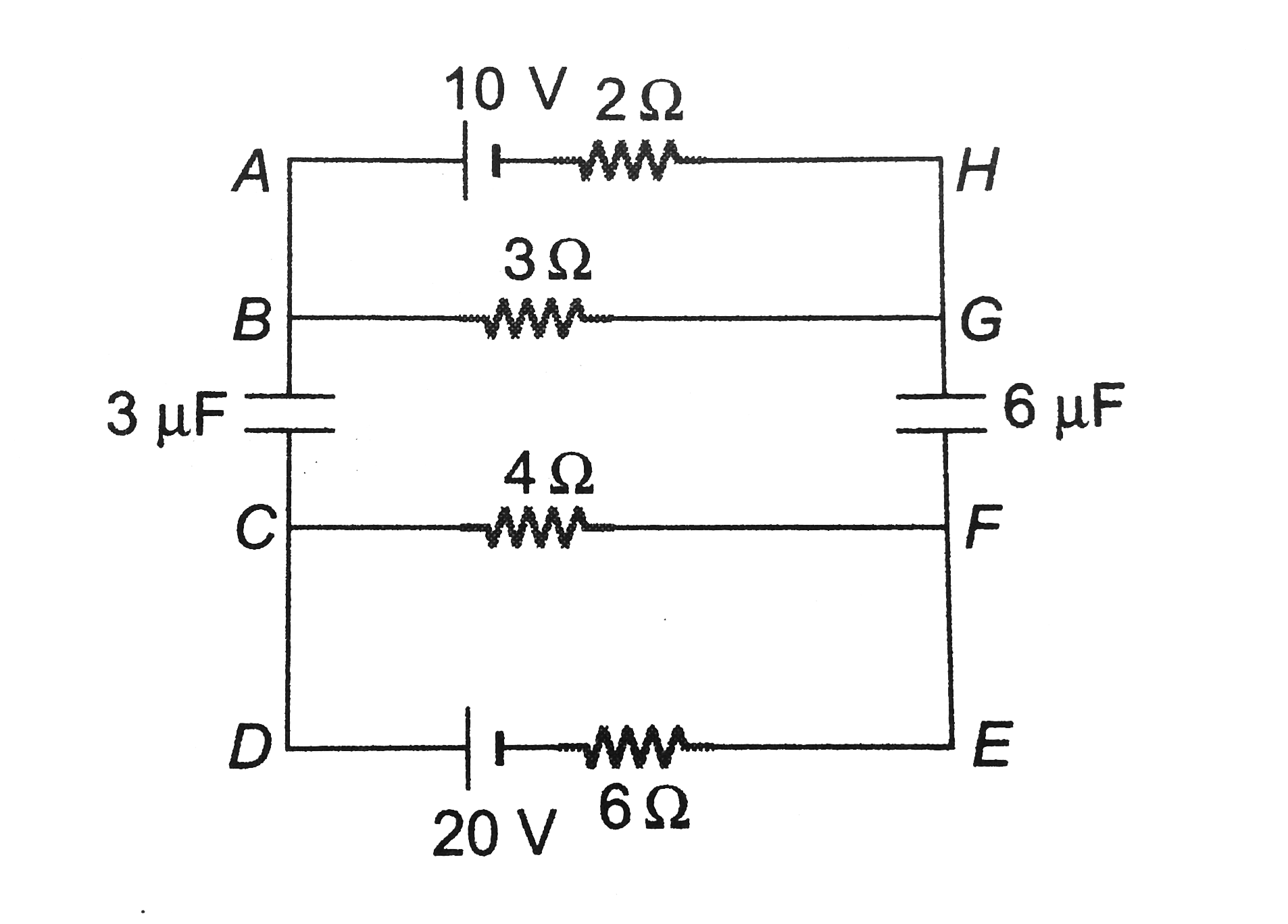
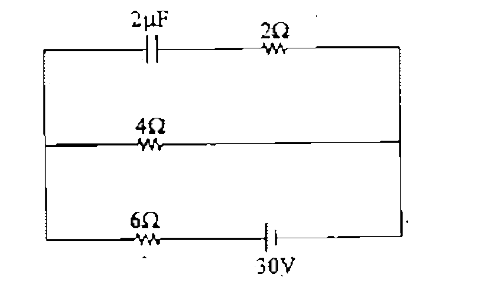
In the circuit shown in figure, find the steady state charges on both the capacitors.
Video Solution
Text Solution
In the steady state, there will be no current flowing through the two capacitors, Therefore, current in lower circuit ABCD is
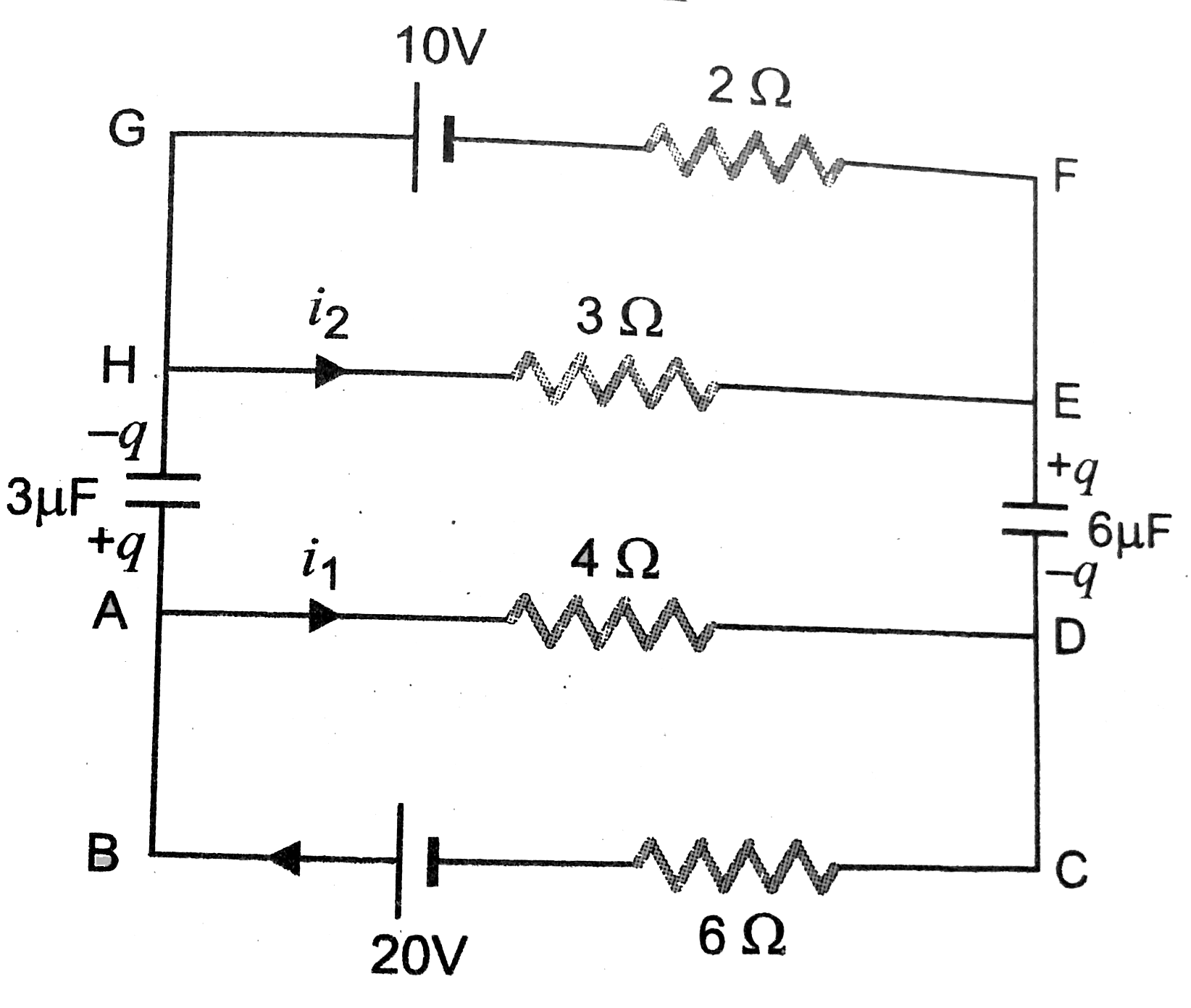
i1=206+4=2A,
and current in upper circuit EFGH is
i2=102+3=2A
Obviously, charges on both capacitors will be same, say q each.
Applying Kirchhoff's law to the loop ADEHAlt we get
4i1−q6×10−6−3i2−q3×10−6=0
or 4i1−3i2=q6×10−6+q3×10−6
or 4×2−3×2=3q6×10−6=q×10−62
q×106=2+2=4
q=4106c=4×10−6c=4μC
|
Similar Questions
Knowledge Check
In the circuit shown in fignre-3.341, find the steady state charge on capacitor C1
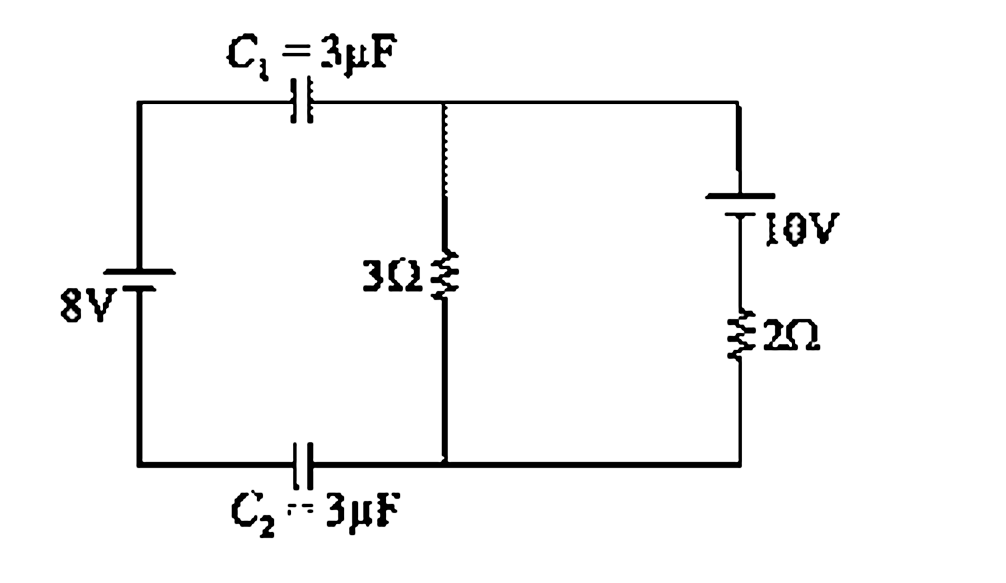 A2μCB3μCC4μCDzero
A2μCB3μCC4μCDzeroIn the circuit shown in the figure, in steady state:

The charge on 5μF capacitor isA30μCB40μCC50μCD60μCFor the circuit arrangement shown in figure, in the steady state condition charge on the capacitor is
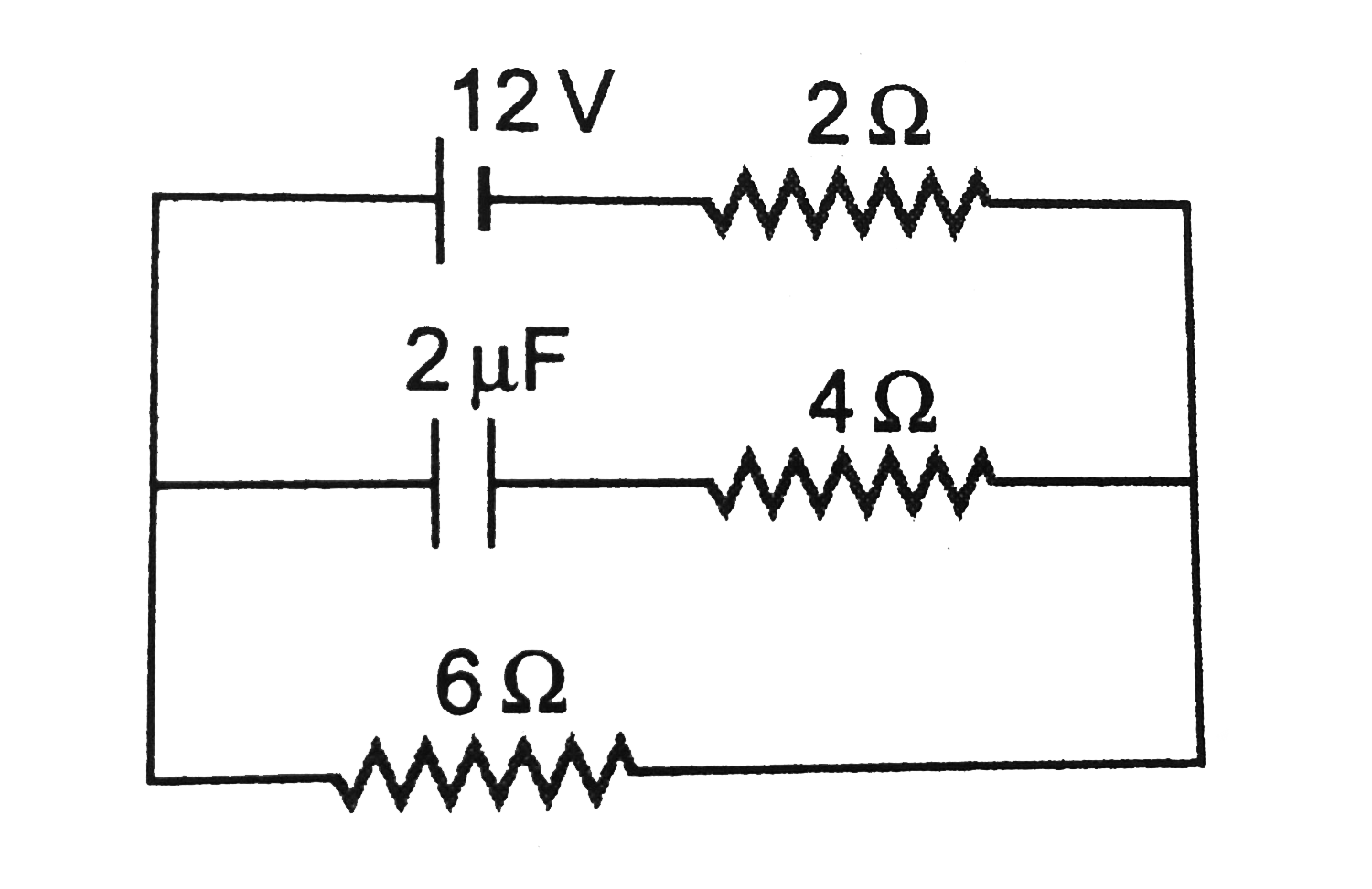 A12μCB14μCC2μCD18μC
A12μCB14μCC2μCD18μC
Find the steady state charge stored in the capacitor.

View SolutionFind the steady state charge stored in the capacitor.
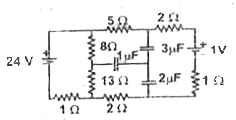
View SolutionAnalyse the circuit shown in the figure in steady state
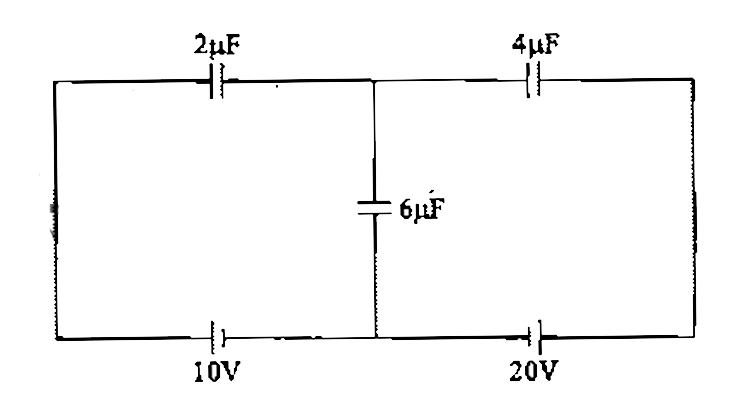
View SolutionIn the circuit shown in figure find the charges on the three capacitors in steady state.
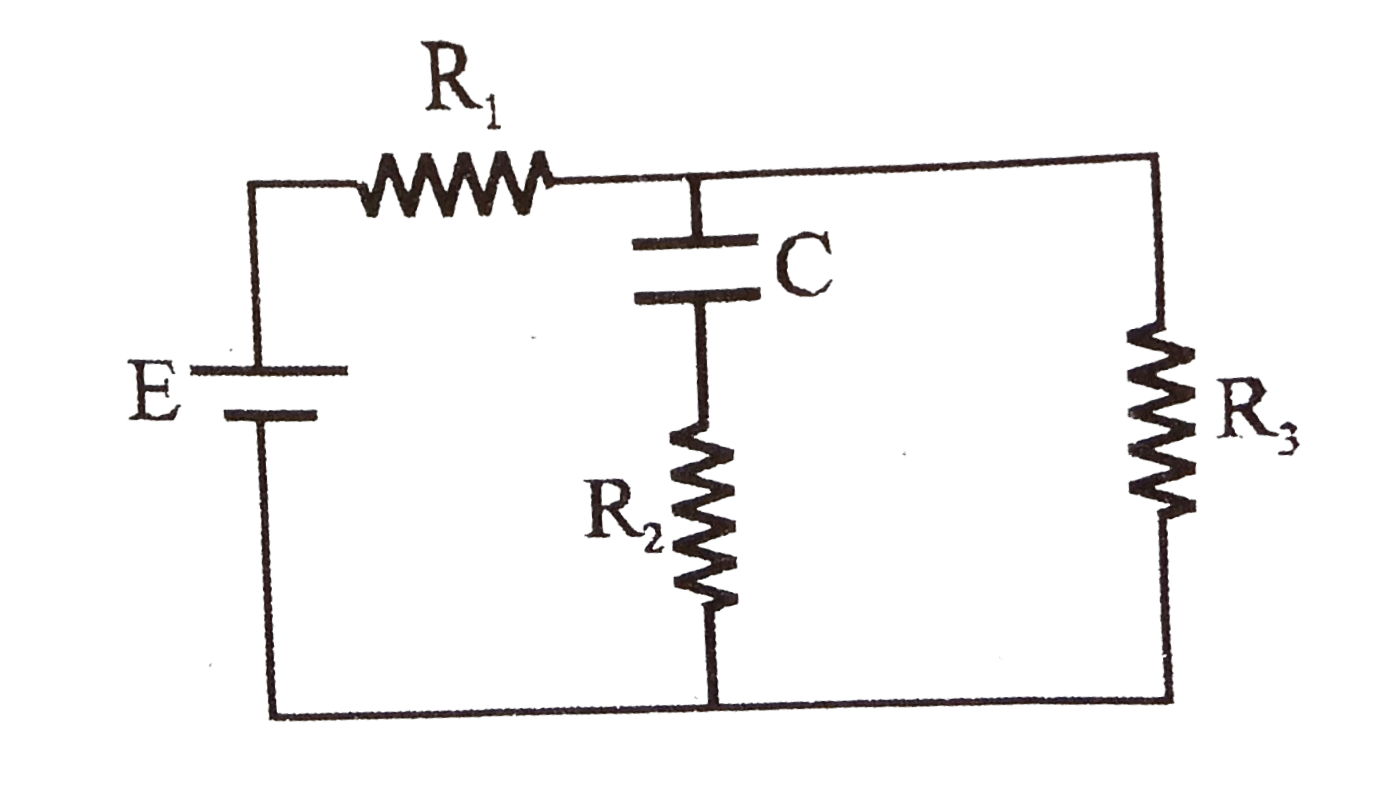
View SolutionIn the circuit shown here, at the steady state, the charge on the capacitor is
View Solution

