In the following figure, the tension in the horizontal cord is 30 N. What is the weight of the boyd B?

40N
30N
20N
10N
The correct Answer is:B

Let T1 be the equilibrium in the cord 1 and T2 be the same in the cord 2.
T2 is resolved into two perpendicular components.
(1) Horizontal component T2sin45∘=30
∴T2=1√2=30∴T2=30√2N
(2) vertical component T2cos45∘=T1=mg
∴ Total weight of B =mg =T2cos45∘
=30√2×1√2=30N
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
As shown in figure the tension in the horizontal cord is 30N. The weight W and tension in the string OA in Newton are
 A30√3,30B30√3,60C60√3,30DNone of these
A30√3,30B30√3,60C60√3,30DNone of these - Question 2 - Select One
The bob of a 0.2 m pendulum describes an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is
AgBg2C√3g2Dg4
As shown in figure the tension in the horizontal cord is 30N. The weight W and tension in the string OA in Newton are
 View Solution
View SolutionAs shown in figure the tension in the horizontal cord is 30N. The weight W and tension in the string OA in Newton are
 View Solution
View SolutionIn the following figure, if the tension in the string AB is 51N, then the tension in the string BC will be :-
View SolutionAll the string in figure are massless. Tension in the horizontal string is 30N. Find W.
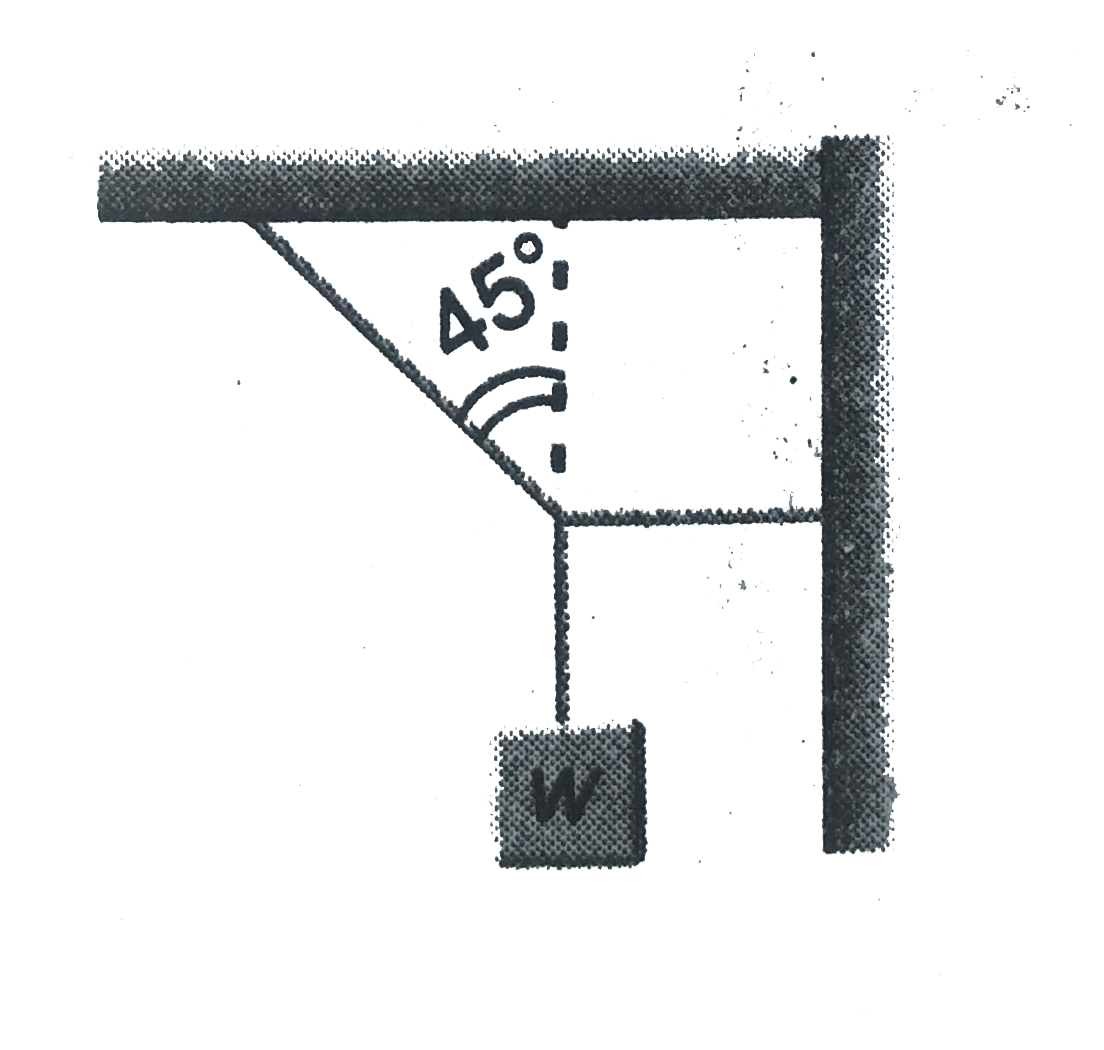 View Solution
View SolutionAll the string in figure are massless. Tension in the horizontal string is 30N. Find W.
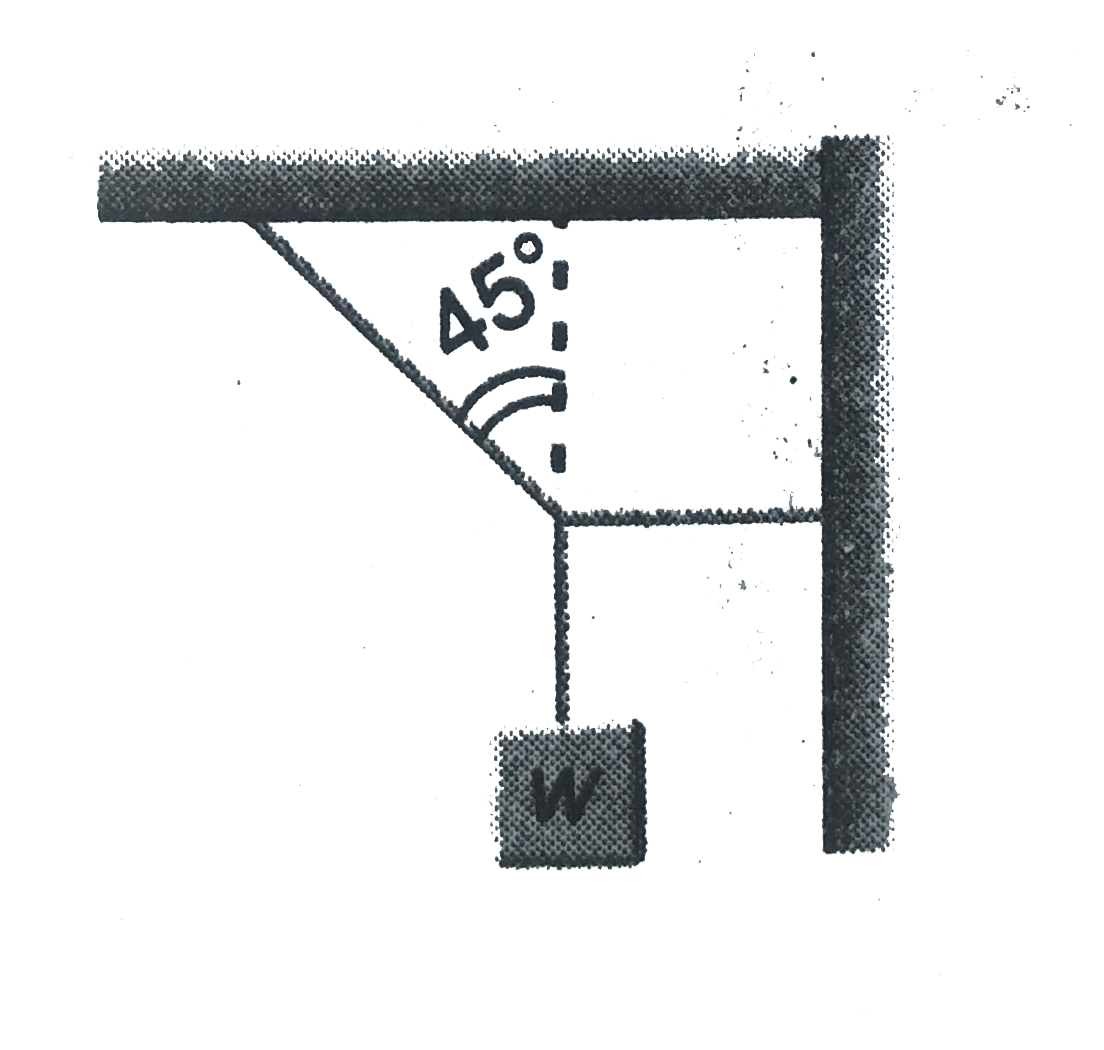 View Solution
View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View Solution


