In the pulley arrangement shown in Fig the pulley p2 is movable .Assuming the coefficient of friction between m and surface to be μ the minimum value of M for which m is at rest is

M=μm2
m=μM2
M=m2μ
m=M2μ
The correct Answer is:a
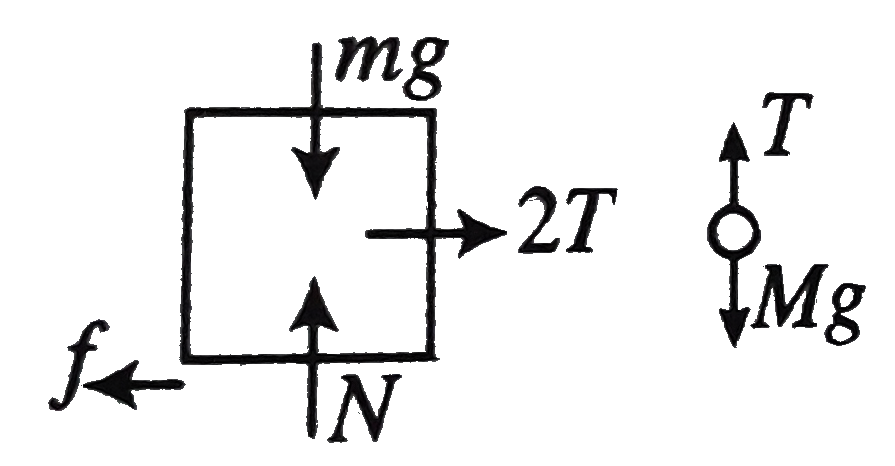
f=2T
and T=Mg
If m be at rest friction will be static
f≤μN
2Mg≤μmg⇒M=μg2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension52videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective21videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
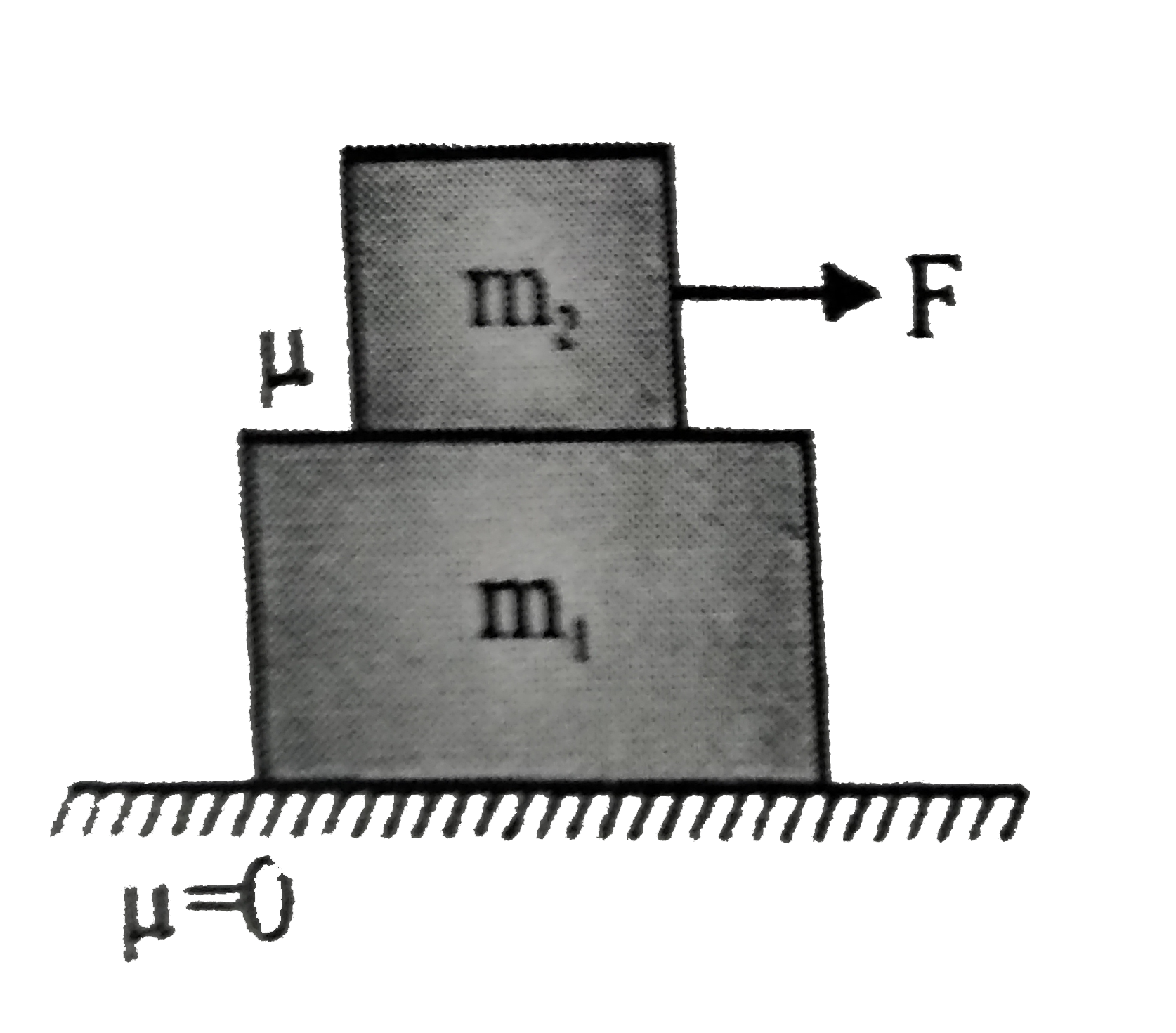
When force F applied on m2 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ… What should be the minimum value of F so that there is no relative motion between m1andm2
 View Solution
View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2 - Question 2 - Select One
A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
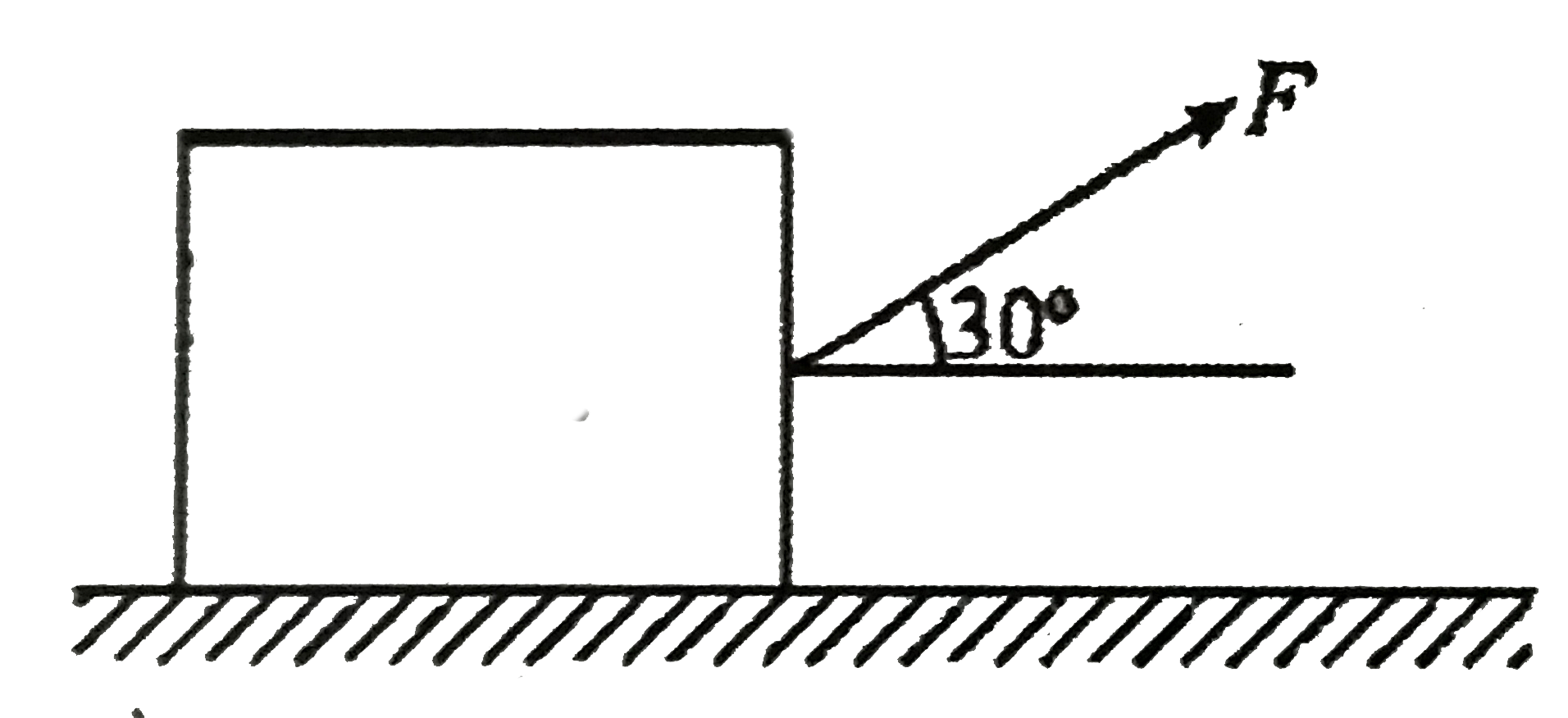 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2] - Question 3 - Select One
A trolley of mass M is attached to a block of mass m by a string passing over a frictionless pulley as shown in the figure. If the coefficient of friction between the horizontal surface and wheels of trolley is μ, then acceleration of the block m and that of trolley M on releasing the system is :-
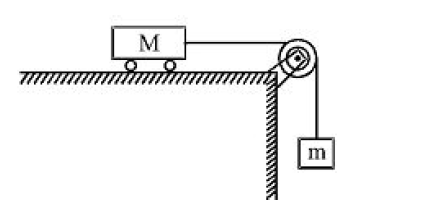 A(μM−mm+μM)gB(m+μMμM−m)gC(μm−Mm+M)gD(m−μMm+M)g
A(μM−mm+μM)gB(m+μMμM−m)gC(μm−Mm+M)gD(m−μMm+M)g
Two blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
 View Solution
View SolutionWhen force F applied on m1 and surface. Is μ1 and the coefficient of friction between m1andm2 is μ2. What should be the minimum value of F so that there is no relative motion between m1andm2.
 View Solution
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
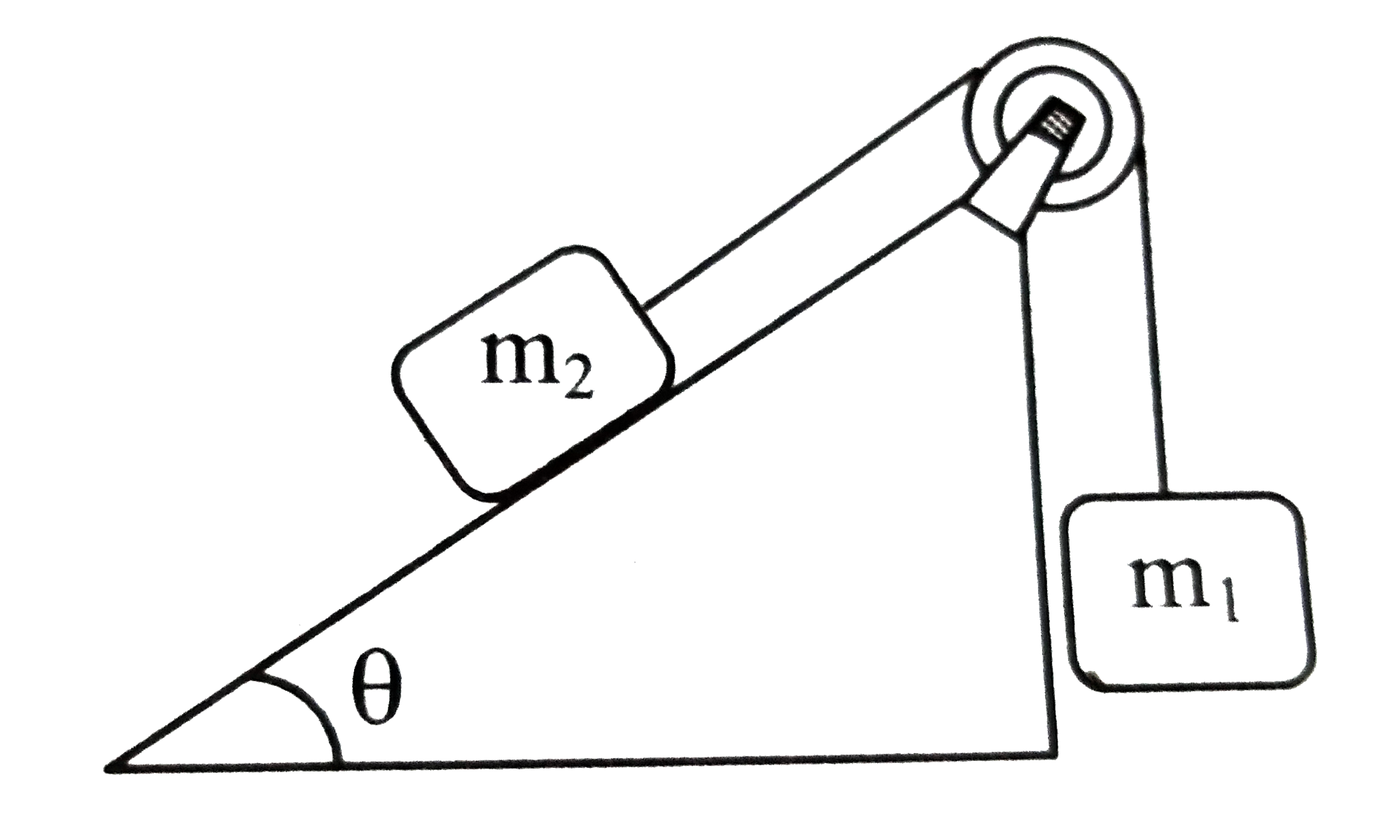 View Solution
View SolutionIn the arrangement shown in figure the cylinder of mass M is at rest on an incline. The string between the cylinder and the pulley (P) is horizontal. Find the minimum coefficient of friction between the incline and the cylinder which can keep the system in equilibrium. Also find the mass of the block. Assume no friction between the pulley (P) and the string.
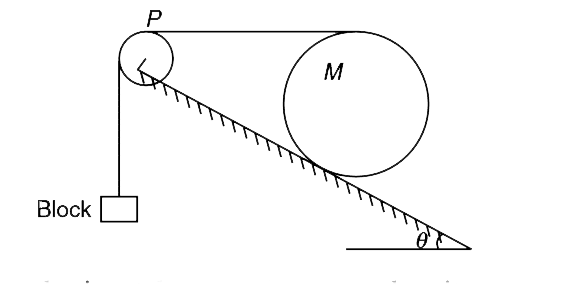 View Solution
View SolutionIn the arrangement shown in the figure, the pulley has a mass 3m, Neglecting friction on the contact surface, the force exerted by the supporting rope AB on the ceiling is
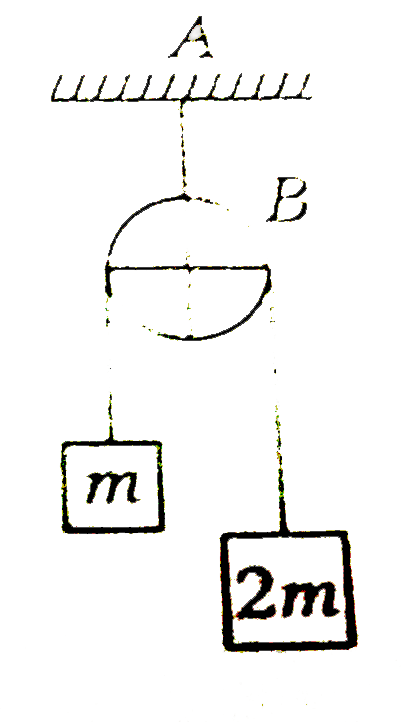 View Solution
View Solution

