In the s-t equation (s=10+20t−5t2) match the following columns.
∣∣
∣
∣
∣
∣
∣∣Column IColumn II(A)Distancec travelled in 3s(p)−20 units(B)Displacement 1 s(q)15 units(C)Initial acceleration(r)25 units(D)Velocity at 4 s(s)−10 units∣∣
∣
∣
∣
∣
∣∣
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the given equation of motion and find the required quantities step by step.
Given:
The equation of motion is:
s=10+20t−5t2
Step 1: Calculate Distance Travelled in 3 seconds (A)
To find the distance travelled in 3 seconds, we substitute t=3 into the equation:
s=10+20(3)−5(32)
Calculating this step-by-step:
- 20(3)=60
- 5(32)=5(9)=45
- Now substitute these values:
s=10+60−45=25 units
Thus, the distance travelled in 3 seconds is 25 units.
Step 2: Calculate Displacement in 1 second (B)
Next, we find the displacement at t=1:
s=10+20(1)−5(12)
Calculating this:
- 20(1)=20
- 5(12)=5(1)=5
- Now substitute:
s=10+20−5=25 units
Thus, the displacement in 1 second is also 25 units.
Step 3: Find Initial Acceleration (C)
The acceleration can be found by first determining the velocity v from the displacement equation:
v=dsdt=ddt(10+20t−5t2)
Differentiating:
- The derivative of 10 is 0
- The derivative of 20t is 20
- The derivative of −5t2 is −10t
Thus, the velocity equation is:
v=20−10t
Now, to find the acceleration a:
a=dvdt=ddt(20−10t)
Differentiating:
- The derivative of 20 is 0
- The derivative of −10t is −10
Thus, the acceleration is:
a=−10 units
Step 4: Calculate Velocity at 4 seconds (D)
Now, we find the velocity at t=4:
v=20−10(4)
Calculating:
v=20−40=−20 units
Summary of Results:
- A: Distance travelled in 3s = 25 units (matches with R)
- B: Displacement in 1s = 25 units (matches with R)
- C: Initial acceleration = -10 units (matches with S)
- D: Velocity at 4s = -20 units (matches with P)
Final Matching:
- A matches with R
- B matches with R
- C matches with S
- D matches with P
The equation of motion is:
s=10+20t−5t2
To find the distance travelled in 3 seconds, we substitute t=3 into the equation:
s=10+20(3)−5(32)
Calculating this step-by-step:
- 20(3)=60
- 5(32)=5(9)=45
- Now substitute these values:
s=10+60−45=25 units
Thus, the distance travelled in 3 seconds is 25 units.
Next, we find the displacement at t=1:
s=10+20(1)−5(12)
Calculating this:
- 20(1)=20
- 5(12)=5(1)=5
- Now substitute:
s=10+20−5=25 units
Thus, the displacement in 1 second is also 25 units.
The acceleration can be found by first determining the velocity v from the displacement equation:
v=dsdt=ddt(10+20t−5t2)
Differentiating:
- The derivative of 10 is 0
- The derivative of 20t is 20
- The derivative of −5t2 is −10t
v=20−10t
Now, to find the acceleration a:
a=dvdt=ddt(20−10t)
Differentiating:
- The derivative of 20 is 0
- The derivative of −10t is −10
a=−10 units
Now, we find the velocity at t=4:
v=20−10(4)
Calculating:
v=20−40=−20 units
- A: Distance travelled in 3s = 25 units (matches with R)
- B: Displacement in 1s = 25 units (matches with R)
- C: Initial acceleration = -10 units (matches with S)
- D: Velocity at 4s = -20 units (matches with P)
- A matches with R
- B matches with R
- C matches with S
- D matches with P
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
In the s−t equations (s=10+20t−5t2) match the following
 View Solution
View SolutionFor the velocity -time graph shown in figure, in a time interval from t=0 to t=6s, match the following:
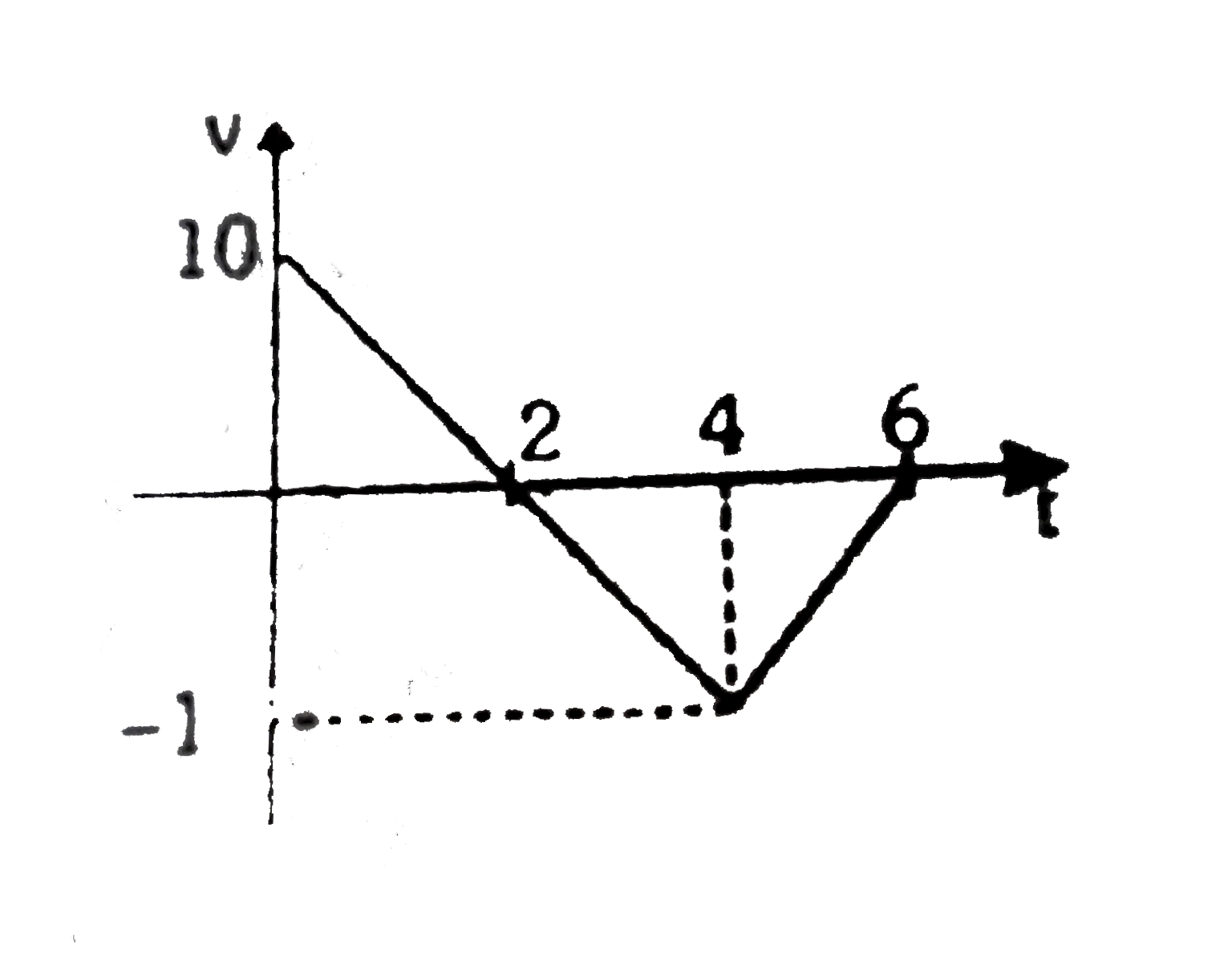
Column IColumn II(A)Change in velocity(p)−5/3SIunit(B)Average acceleration(q)−20SIunit(C)Total displacement(r)−10SIunit(D)Acceleration ay t=3s(s)−5SIunitView SolutionMatch the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)d v/dt(p)Acceleration(B)d|v|/dt(q)Magnitude of acceleration(C)drdt(r)Velocity(D)∣∣drdt∣∣(s)Magnitude of velocity(t)Rate of change of speed∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunitsView SolutionIn the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unitView SolutionIn the diagram shown in figure, match the following (g=10m/s2)

Column-IColoumn-II(A)Acceleration of 2kg block(P)8 Si unit(B)Net force on 3kg block(Q)25 SI unit(C)Normal reaction between 2 kg and 1kg(R)2 SI unit(D)Normal reaction between 3 kg and 2kg (S) 45 SI unit(T) NoneView SolutionIn the circuit shown in figure, E = 10 V, r = 1Ω,
R = 4Ω and L = 5H. The circuit is closed at time t = 0.
Then, match the following two columns.
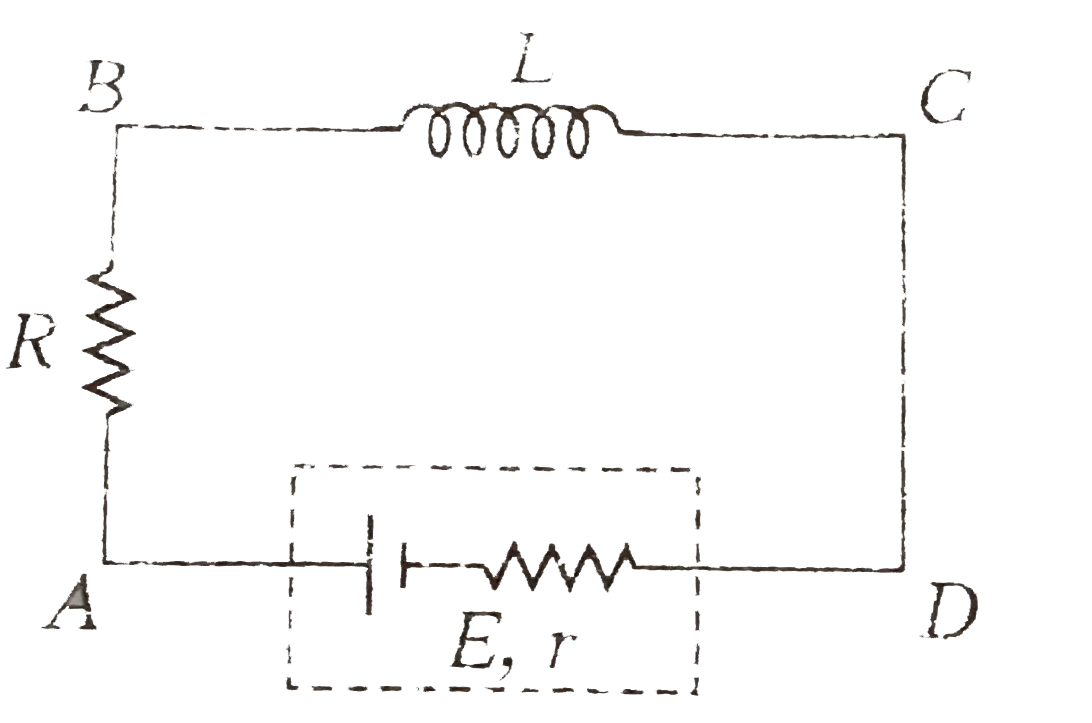
Column IColumn IIA.VAD at t = 0p4VB.VBC at t = 0q8VC.VAB at t =∞r.0VD.VAD at t=∞s.10VView SolutionMatch the column - I with column - II
Column - IColumn - II1.MicronutrientsA.Fe2.Macronutrients B.Nitrosomonas3.NitrificationC.S4.DenitrificationD.ThiobacillusView SolutionIn y=Asinωt+Asin(ωt+2π3)
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column-IColumn-II(A)Motion(p)is periodic but no SHM(B)Amplitude(q)is SHM(C)Initial phase(r)A(D)Maximum velocity(s)π/3(t)ωA/2(u)None∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)NoneView Solution
