It is given that the mass m of the largest stone that can be moved by the folowing river depends upon the velocity v, density ρ and acceleration due gravity g. Using dimensions show that m=kv6ρg3.
To solve the problem, we need to show that the mass m of the largest stone that can be moved by the river can be expressed in the form:
m=kv6ρg3
where k is a dimensionless constant, v is the velocity, ρ is the density, and g is the acceleration due to gravity.
1. Identify the Variables and Their Dimensions:
- Mass m: Dimension (M)
- Velocity v: Dimension (LT−1)
- Density ρ: Dimension (ML−3)
- Acceleration due to gravity g: Dimension (LT−2)
2. Assume a Relationship:
We assume that the mass m can be expressed as a function of the variables v, ρ, and g:
m=kvxρygz
where k is a dimensionless constant and x,y,z are the powers we need to determine.
3. Write the Dimensions of Each Term:
- The dimension of vx is (LT−1)x=(LxT−x)
- The dimension of ρy is (ML−3)y=(MyL−3y)
- The dimension of gz is (LT−2)z=(LzT−2z)
4. Combine the Dimensions:
The combined dimension of the right-hand side is:
(MyLx−3y+zT−x−2z)
5. Set Up the Equation:
Since the left-hand side has the dimension of mass (M), we equate the dimensions:
(M1L0T0)=(MyLx−3y+zT−x−2z)
This gives us three equations:
- For mass: y=1
- For length: x−3y+z=0
- For time: −x−2z=0
6. Solve the Equations:
From y=1:
- Substitute y into the second equation:
x−3(1)+z=0⟹x+z=3
- From the third equation:
−x−2z=0⟹x=−2z
Substitute x=−2z into x+z=3:
−2z+z=3⟹−z=3⟹z=−3
Now substitute z back to find x:
x=−2(−3)=6
7. Final Values:
We have:
- x=6
- y=1
- z=−3
8. Substitute Back:
Substitute x,y,z back into the assumed relationship:
m=kv6ρ1g−3
This can be rewritten as:
m=kv6ρg3
Conclusion:
Thus, we have shown that the mass m of the largest stone that can be moved by the river is given by:
m=kv6ρg3
- Mass m: Dimension (M)
- Velocity v: Dimension (LT−1)
- Density ρ: Dimension (ML−3)
- Acceleration due to gravity g: Dimension (LT−2)
We assume that the mass m can be expressed as a function of the variables v, ρ, and g:
m=kvxρygz
where k is a dimensionless constant and x,y,z are the powers we need to determine.
- The dimension of vx is (LT−1)x=(LxT−x)
- The dimension of ρy is (ML−3)y=(MyL−3y)
- The dimension of gz is (LT−2)z=(LzT−2z)
The combined dimension of the right-hand side is:
(MyLx−3y+zT−x−2z)
Since the left-hand side has the dimension of mass (M), we equate the dimensions:
(M1L0T0)=(MyLx−3y+zT−x−2z)
- For mass: y=1
- For length: x−3y+z=0
- For time: −x−2z=0
From y=1:
- Substitute y into the second equation:
x−3(1)+z=0⟹x+z=3
- From the third equation:
−x−2z=0⟹x=−2z
−2z+z=3⟹−z=3⟹z=−3
Now substitute z back to find x:
x=−2(−3)=6
We have:
- x=6
- y=1
- z=−3
Substitute x,y,z back into the assumed relationship:
m=kv6ρ1g−3
This can be rewritten as:
m=kv6ρg3
Thus, we have shown that the mass m of the largest stone that can be moved by the river is given by:
m=kv6ρg3
Topper's Solved these Questions
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
10 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - LONG ANSWER QUESTIONS
3 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
Similar Questions
Assuming that the mass m of the largest stone that can be moved by a flowing river depends upon the velocity v of the water , its density ρ , and the acceleration due to gravity g . Then m is directly proportinal to
View SolutionAssuming that the mass m of the largest stone that can be moved by a flowing river depends upon the velocity υ, of water, its density ρ and acceleration due to gravity g, then m is directly proportional to
View SolutionAssume that the largest stone of mass 'm' that can be moved by a flowing river depends upon the velocity of flow v, the density d & the acceleration due to gravity g. I 'm' varies as the Kth power of the velocity of flow, then find the value of K.
View SolutionThe velocity of water wave v may depend on their wavelength λ, the density of water ρ and the acceleration due to gravity g. The method of dimensions gives the relation between these quantities as
View SolutionExperiments reveal that the velocity v of water waves may depend on their wavelength λ, density of water ρ, and acceleration due to gravity g. Establish a possible relation between vandλ,g,ρ.
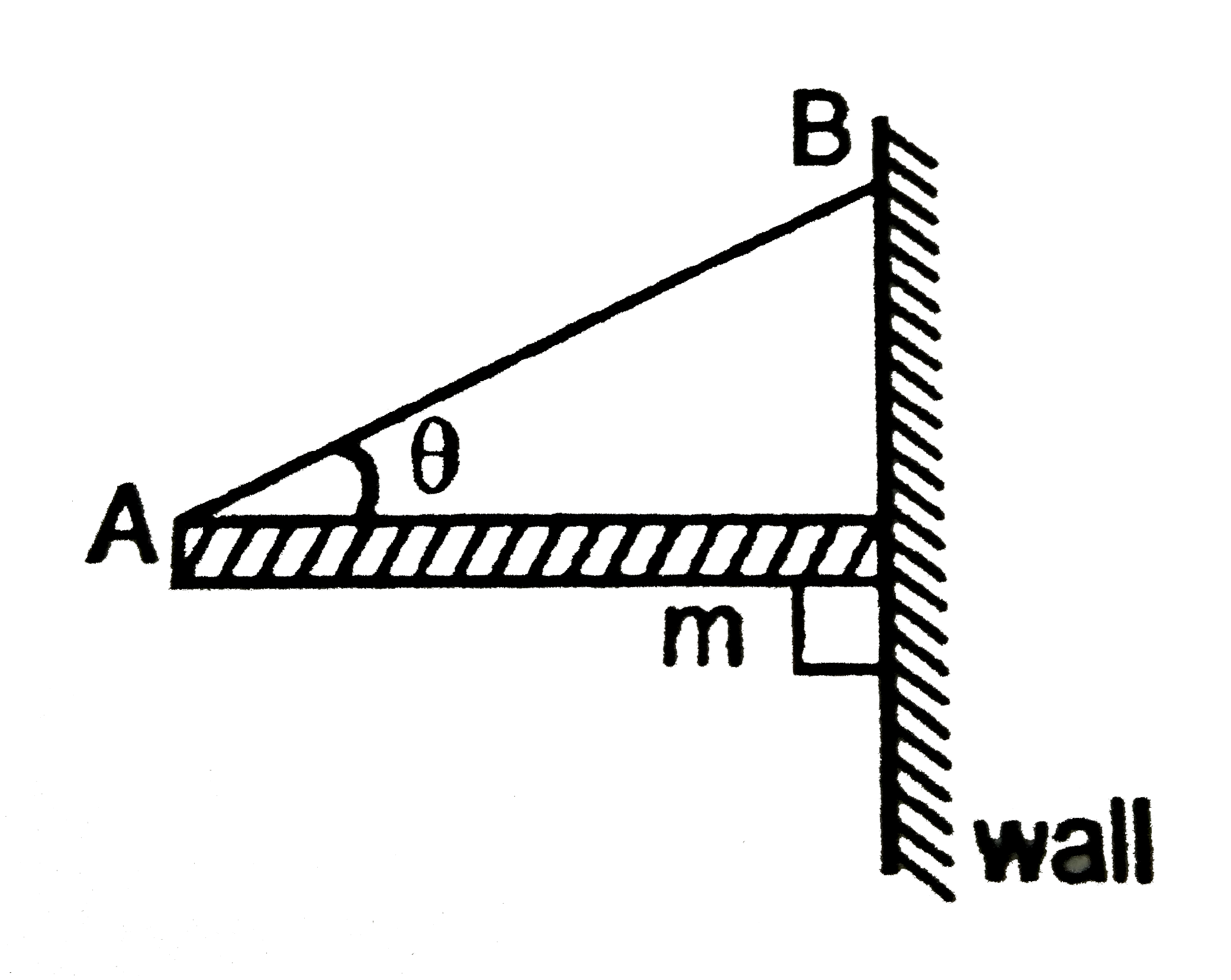
View SolutionA rod of mass m is supported by string AB and friction due to wall. Then friction force on rod due to wall is :
(g= acceleration due to gravity )
View SolutionThe buoyant force F acting on a body depends on the density of medium ρ, volume of body immerese V and acceleration due to gravity g. Establish the relation using method of dimensions.
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionThe condition for a uniform spherical mass m of a radius r to be a black hole is [G =gravitational constant and g=acceleration due to gravity]
View SolutionDerive an expression for the time period (T) of a simple pendulum which may depend upon the mass (m) of the bob, length (l) of the pendulum and acceleration due to gravity (g).
View Solution
